Lektsii_Rubleva_1 / Гл 01 Вступ до анал_зу / Пар 1-04 Посл_довност_

Лема 1.	(Про обмежену послідовність).
	Якщо , то .

Доведення. Якщо виконуються умови леми, то нерівність не справджується лише, можливо, для скінченої кількості членів послідовності . Позначимо тоді , . . Тоді легко зрозуміти, що , тобто послідовність - обмежена.

Лема доведена.

Лема 2.	(Про модуль обмеженої послідовності).
	Якщо , то .

Доведення. З умови обмеженості . Позначимо , то .

Лема доведена.

Наслідок.	(Еквівалентне означення обмеженої послідовності).
	.

Теорема 7.	(Дії над символами Ландау).
1.	(сума двох обмежених – обмежена);
2.	(сума двох нескінченно малих – нескінченно мала);
3.	;
4.	(добуток двох обмежених – обмежена);
5.	(добуток двох нескінченно малих – нескінченно мала);
6.	(добуток нескінченно малої на обмежену є нескінченно малою).

Доведення. Доведемо деякі два з них, наприклад 2 та 6.

2. Позначимо ( ) і ( ) , а тому .

6. Позначимо ( ) і ( ) .

Теорема доведена.

Приклад 4.	Дослідити на збіжність послідовності: , .
	.

Наслідок.	(Інші дії над символами Ландау).
1.	;
2.	;
3.	;
4.	.

Теорема 8.	(Арифметичні дії над збіжними послідовностями).
	Якщо , то
1.	;
2.	;
3.	;
4.	.

Доведення. З теореми 6 запишемо послідовності , тоді одержимо. твердження 1. доведено.

З теореми 4 послідовності обмежені, тобто дорівнюють , а тому , твердження 2. доведено.

Оскільки , то , а тому (лема 1), тому і твердження 3. доведеною.

Тепер з останніх двох властивостей одержимо: .

Теорема доведена.

Зауваження 1.	Теорема 8 залишається чинною у випадку, коли та не виникає невизначеності.
Зауваження 2.	Послідовність нескінченно велика тоді і тільки тоді, коли .

Приклад 5.

Знайти границю: .

Якщо , то поділимо чисельник та знаменник на : ; Якщо , то , а тому при ; Якщо , то поділимо чисельник та знаменник на : .

Розглянемо такі три послідовності , , . Проведемо дослідження стосовно їх збіжності, при цьому спробуємо це зробити якомога більш різними шляхами. Почнемо з . З формули бінома Ньютона одержимо:

, (1)

як легко побачити, порівнюючи відповідні доданки у і , ця послідовність зростаюча. Крім того з нерівності (1) легко одержати таке обмеження: , а тому як і є монотонними та обмеженими (монотонність очевидна). Тому вони обидві збіжні. Границю послідовності називають числом . Знову розглянемо праву частину (1). Якщо зафіксувати деяке , ми одержимо:

. (2)

Зробимо в цій нерівності граничний перехід при , ми одержимо, що ліва частина прямує до , а права до виразу . З теореми про перехід до границі в нерівностях одержимо, що , а тому з теореми про двох поліцаїв .

Для різноманіття проведемо дослідження останньої послідовності іншим чином. монотонно спадна, крім того з ланцюгу нерівностей ми маємо: тобто вона й обмежена, а тому збіжна. З теореми про границю добутку одержимо: , таким чином усі розглянуті послідовності збігаються до .

Теорема 9.	(Границя показникової та логарифмічної послідовностей).
	Нехай . Тоді послідовність збігається до , а послідовність до (при ).

Доведення. Спочатку для показникової послідовності. При все очевидно. Нехай, наприклад, . Тоді виберемо довільне і розглянемо ланцюг нерівностей: . Із збіжності до слідує, що для … , що й треба було довести. Випадок розглядається аналогічно.

Так само випадок логарифмічної послідовності розглянемо при . Знову виберемо довільне і розглянемо ланцюг нерівностей: . І знову з умови слідує, що … , що й треба довести. Другий випадок розглядається аналогічно.

Теорема доведена.

Наслідок 1.	(Границя степенево-показникової послідовності).
	Нехай , а . Тоді .

Доведення. Все слідує з перетворень: .

Наслідок доведено.

Наслідок 2.	(Границя степеневої послідовності).
	Нехай , тоді .

Доведення слідує з попереднього наслідку, якщо покласти , .

Наслідок 3.	(Границя показникової послідовності на нескінченності).
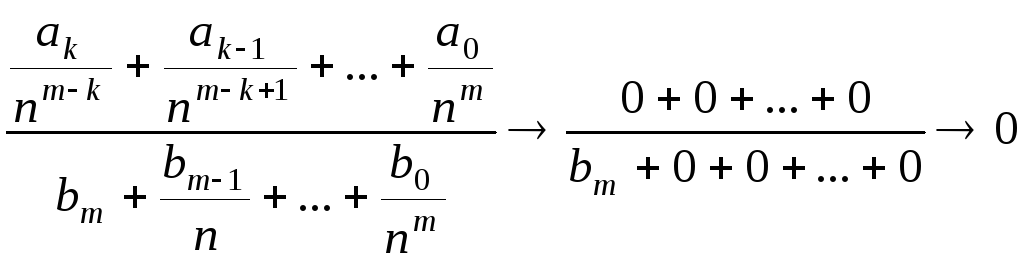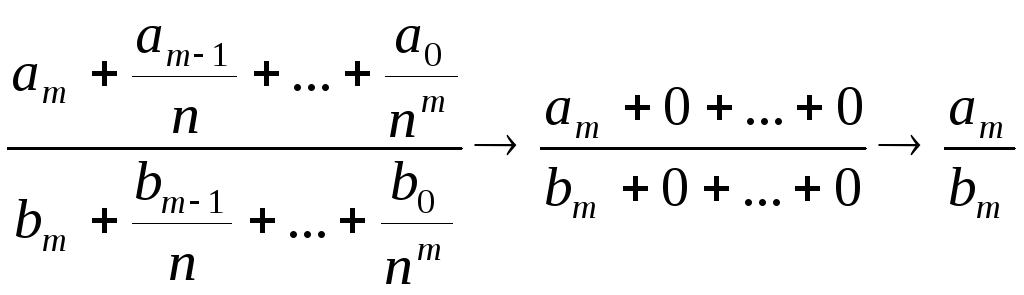	Нехай , тоді якщо , то , а якщо , то при .