Lektsii_Rubleva_1 / Гл 01 Вступ до анал_зу / Пар 1-08 Неперервн_сть

, , . (1)

Властивості.	(Базової функції ).
1)	Функція визначена в кожній точці сегменту .
2)	Функція неспадна.
3)	Функція неперервна.

Доведення. 1) Перша властивість безпосередньо слідує з існування супремуму для обмеженої множини. 2) Друга з властивості супремуму та з визначення функції . 3) Остання властивість доводиться методом від супротивного. Якщо припустити, що функція розривна, то з монотонності ми робимо висновок, що ця точка розриву першого роду. Тобто на проміжку існує інтервал, вільний від значень функції, але вже на викинутих інтервалах ми визначили значення функції, як скрізь щільні, а тому не може бути подібного інтервалу без значень. Одержана суперечність завершує доведення властивостей.

Тепер визначимо функцію Кантора , як функцію, що визначається за правилом:

(2)

Властивості.	(Функції Кантора ).
1)	Функція зростаюча.
2)	Функція неперервна.

Функція називається раціональною.

Властивості.	(Неперервних функцій).
1)	Алгебраїчний многочлен є неперервною функцією ;
2)	Кожна раціональна функція є неперервною : ;
3)	Функції , , , , , , неперервні ;

Доведення. Розглянемо, наприклад, функцію : тоді - знайшли потрібне . Аналогічно для решти функцій.

Властивості.	(Неперервних функцій).
4)	Функції , , неперервні на своїх множинах визначення.

Множина називається компактною в собі або компактом, якщо з будь-якої послідовності точок з можна виділити підпослідовність збіжну до деякої точки .

Теорема 5.	(Критерій компактності в собі).
	Множина є компактом тоді і тільки тоді, коли вона одночасно замкнена і обмежена.

Доведення. Необхідність. - компакт. Спочатку покажемо від супротивного обмеженість компакту. Якщо не обмежена, то : з неї не можна виділити підпослідовність, збіжну до деякої точки . - обмежена множина. Припустимо, що не замкнена : . Але тоді будь-яка підпослідовність . Суперечність з означенням компакту.

Необхідність доведена.

Достатність. Нехай - замкнена і обмежена. Розглянемо довільну послідовність . Вона обмежена (за теоремою Больцано-Вейєрштрасса), внаслідок замкненості - гранична точка .

Достатність доведена.

Приклад 5.	На можна навести такі приклади:
	- компакти;
	- не ком пакти.

Наслідок.	(Екстремальні властивості компакту).
	Нехай - компакт, тоді в є найбільший та найменший елементи.

Доведення. - замкнена і обмежена, а далі все маємо за наслідком з відповідної теореми про повний простір.

Наслідок доведено.

Теорема 6.	(Неперервний образ компакта).
	Нехай неперервна на функція, де - компакт. Тоді і множина - компакт.

Доведення. Розглянемо довільну послідовність , тоді : . Тоді - підпослідовність: . З неперервності : - компакт.

Теорема доведена.

Наслідок.	(Теорема Вейєрштрасса).
	Нехай неперервна на компакті функція. Тоді вона приймає найменше та найбільше значення.

Доведення безпосередньо слідує з останнього наслідку та теореми 6.

Теорема 7.	(Неперервність оберненої функції).
	Якщо , - компакт, якщо - неперервна та оборотна на , то також неперервна функція на .

Доведення. Нехай - довільна послідовність, що збігається до . Розглянемо послідовність , і нехай її часткова границя . З неперервності слідує, що є частковою границею . Тобто всі часткові границі дорівнюють також неперервна в точці . Оскільки - довільна точка з - неперервна.

Теорема доведена.

Наслідок.	(Властивості оберненої функції).
	Якщо функція строго монотонна і неперервна на компакті , то обернена їй функція існує, неперервна і монотонна на компакті .

Доведення. Достатньо показати існування та монотонність оберненої функції. Нехай зростаюча на . Тоді : . Покладемо . То, що вона дійсно обернена до , очевидно. Покажемо від супротивного, що вона зростаюча. Якщо : і , тоді, якщо позначити , але суперечність.

Наслідок доведення.

Властивості.		(Неперервних функцій).
5)	Функція неперервна на області визначення.

Нехай . Нерівність (або інша властивість) називається стійкою, якщо існує такий окіл в , що 9виоконується наведена властивість).

Теорема 8.	(Про стійкість нерівності).
	Нехай функція неперервна в точці - граничній для множини . Тоді такого, що , ця нерівність стійка.

Доведення. Припустимо, що нерівність нестійка. Тоді : . Зрозуміло, що , тоді переходячи до границі в останній нерівності, та використовуючи неперервність на одержимо суперечність.

Теорема доведена.

Нехай , , , . Коливанням функції на множині називається різниця . Якщо , кажуть, що має нескінчене коливання на .

Теорема 9.	(Існування скінченого коливання).
	Якщо : виконується нерівність: , то і .

Доведення. Перепишемо умову теореми у вигляді: . Якщо зафіксувати , то ця нерівність має місце обмежена , .

Нехай і . З властивостей верхньої та нижньої меж ,: .

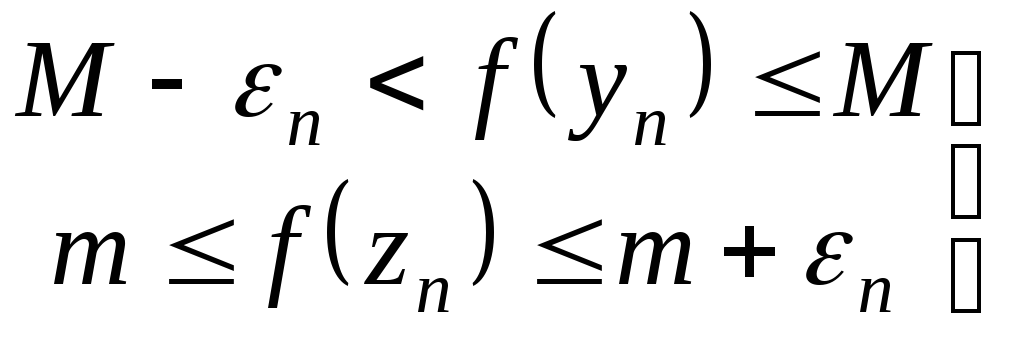
З нерівностей , . Тому : .

Теорема доведена.

Теорема 10.	(Критерій Бера неперервності функції в точці).
	Функція неперервна в точці , граничній для тоді і тільки тоді, коли на множині .,

Доведення. Необхідність. Якщо неперервна в точці , то , .

Необхідність доведена.

Достатність. Нехай : : .

Достатність доведена. Теорема доведена.

Нехай , - гранична точка множини , , . Коливанням функції у точці називається границя: .

Наслідок.	(Критерій неперервності через коливання в точці).
	Для того, щоб була неперервною в точці , граничній для , необхідно і достатньо, щоб виконувалась умова .