
- •МОДУЛЬ 2. КОМБІНАТОРИКА
- •Історична довідка
- •Слайди лекцій
- •Практичні заняття
- •Тема 1: Комбінації, розміщення, перестановки без повторень.
- •Тема 2: Комбінації, розміщення, перестановки з повтореннями.
- •Тема 3: Комбінаторні тотожності.
- •Тема 4: Рекурентні співвідношення
- •Тема 5: Твірні функції та рекурентні співвідношення
- •Література до модуля 2.
- •Основна
- •Додаткова
- •МОДУЛЬ 3. АЛГОРИТМИ
- •Історична довідка
- •Слайди лекцій
- •Практичні заняття
- •Тема 1: Нормальні алгоритми Маркова.
- •Тема 2: Методи побудови ефективних алгоритмів.
- •Тема 3: Алгоритми сортування.
- •Література до модуля 3.
- •Основна
- •Додаткова
- •Українсько-англійський тематичний словник з дискретної математики
- •Розділи «Комбінаторика» та «Теорія алгоритмів».

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ІМЕНІ ТАРАСА ШЕВЧЕНКА
Іванов Є.О., Ченцов О.І., Шевченко В. П.
ДИСКРЕТНА МАТЕМАТИКА
РОБОЧИЙ ЗОШИТ
з українсько-англійським тематичним словником
Комбінаторика Теорія алгоритмів
КИЇВ-2011
Іванов Є.О., Ченцов О.І., Шевченко В. П.
Дискретна математика. Робочий зошит з українсько-англійським тематичним словником. Комбінаторика. Теорія алгоритмів. – К., 2011. – 75 с.
У книзі подано матеріали для вивчення другого та третього модулів «Комбінаторика» та «Теорія алгоритмів» курсу дискретної математики студентами 1 курсу факультету кібернетики напрямків підготовки «Інформатика» та «Програмна інженерія».
Робочий зошит призначено для ведення у ньому конспекту з дискретної математики, для полегшення і прискорення конспектування тут наведені всі слайди лекцій, що позбавляє студента необхідності перемальовувати формули і рисунки, записувати з голосу означення і формулювання. Крім того у зошиті подані плани семінарських занять (теоретичні питання, умови аудиторних, домашніх і додаткових завдань), література до відповідного модулю курсу, українсько-англійський тематичний словник, який полегшить користування іноземною літературою з дискретної математики.
Всі матеріали зошиту можна знайти в електронній бібліотеці факультету кібернетики за адресою: http://www.unicyb.kiev.ua/Library/DM .
Рецензенти:
О.А.Летичевський, академік НАН України, д-р фіз.-мат. наук; А.Ю.Дорошенко, д-р фіз.-мат. наук, П.О.Бех, канд.філол.наук
Затверджено Радою факультету кібернетики 21 червня 2011 року, протокол № 11.
Друкується за авторською редакцією.
ЗМІСТ
МОДУЛЬ 2. КОМБІНАТОРИКА ..................................................................... |
2 |
Історична довідка....................................................................................... |
2 |
Слайди лекцій ............................................................................................. |
5 |
Практичні заняття ................................................................................. |
33 |
Тема 1: Комбінації, розміщення, перестановки без повторень........... |
33 |
Тема 2: Комбінації, розміщення, перестановки з повтореннями........ |
35 |
Тема 3: Комбінаторні тотожності.......................................................... |
36 |
Тема 4: Рекурентні співвідношення...................................................... |
38 |
Тема 5: Твірні функції та рекурентні співвідношення.......................... |
40 |
Література до модуля 2.......................................................................... |
41 |
Основна ................................................................................................. |
41 |
Додаткова.............................................................................................. |
41 |
МОДУЛЬ 3. АЛГОРИТМИ............................................................................ |
42 |
Історична довідка..................................................................................... |
42 |
Слайди лекцій ........................................................................................... |
46 |
Практичні заняття ................................................................................. |
68 |
Тема 1: Нормальні алгоритми Маркова............................................... |
68 |
Тема 2: Методи побудови ефективних алгоритмів.............................. |
69 |
Тема 3: Алгоритми сортування............................................................. |
70 |
Література до модуля 3.......................................................................... |
70 |
Основна ................................................................................................. |
70 |
Додаткова.............................................................................................. |
71 |
УКРАЇНСЬКО-АНГЛІЙСЬКИЙ ТЕМАТИЧНИЙ СЛОВНИК З ДИСКРЕТНОЇ |
|
МАТЕМАТИКИ....................................................................................... |
72 |
Розділи «Комбінаторика» та «Теорія алгоритмів».............................. |
72 |
1
МОДУЛЬ 2. КОМБІНАТОРИКА
Історична довідка
Комбінаторика, комбінаторний аналіз, комбінаторна математика - розділ математики, присвячений розв’язанню задач вибору й розташування елементів деякої, звісно скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції з елементів вихідної множини, називаною комбінаторною конфігурацією. Тому можна сказати, що метою комбінаторики є вивчення комбінаторних конфігурацій, зокрема, питання їхнього існування, алгоритми побудови, розв’язання задач на перерахування.
Розрізнені комбінаторні задачі людство вирішувало з незапам'ятних часів. Деякі елементи комбінаторики були відомі в Індії ще в II ст. до н.е. Індійці вміли обчислювати числа, які зараз називають "сполучення". В XII ст. Бхаскара обчислював деякі види комбінацій і перестановок. Припускають, що індійські вчені вивчали комбінації у зв'язку із застосуванням їх у поетиці, науці про структуру вірша й поетичних добутків. Наприклад, у зв'язку з підрахунком можливих сполучень ударних (довгих) і ненаголошених (коротких) складів стопи з n складів.
Як наукова дисципліна, комбінаторика сформувалася в XVII ст. Термін "комбінаторика" був уведений у математичний побут знаменитим Лейбніцем. В 1666 році Лейбніц опублікував "Міркування про комбінаторне мистецтво". У своєму творі Лейбніц, вводячи спеціальні символи, терміни для підмножин і операцій над ними, знаходить всі k-комбінації з n елементів, виводить властивості комбінацій, будує таблиці комбінацій до n=k=12, після чого міркує про застосування комбінаторики до логіки, арифметики, до проблем віршування й ін.
ВXVIII столітті до рішення комбінаторних задач зверталися видатні математики. Так, Леонард Эйлер розглядав задачі про розбивку чисел, про паросполучення, про циклічні розміщення, про побудову магічних і латинських квадратів.
В1713 році був опублікований твір Я. Бернуллі "Мистецтво припущень", у якому з достатньою повнотою були викладені відомі на той час комбінаторні факти. Твір складався з 4 частин, комбінаториці була присвячена друга частина, в якій одержано формули:
для числа перестановок з n елементів,
для числа комбінацій (називаного Я. Бернуллі класовим числом) без повторень і з повтореннями,
для числа розміщень із повтореннями й без повторень.
Для виводу формул автор використовував прості й наочні мето ди, супроводжуючи їх численними таблицями й прикладами. Твір Я. Бернуллі перевершив роботи його попередників і сучасників систематичністю, простотою методів, строгістю викладу й протягом XVIII століття користувалося популярністю не тільки як серйозний науковий трактат, але і як навчально-довідкове видання. У роботах Я. Бернуллі й Лейбніца ретельно вивчені властивості комбінацій, розміщень, перестановок. Перераховані комбінаторні об'єкти відносяться до основних комбінаторних конфігурацій. Комбінаторика, пройшовши досить довгий шлях
2
розвитку, сформувавши власні методи дослідження, з одного боку, широко використовується при рішенні задач алгебри, геометрії, аналізу, з іншого боку, сама використовує геометричні, аналітичні й алгебраїчні методи дослідження.
Сучасна символіка сполучень була запропонована різними авторами навчальних посібників лише в XIX ст.
В XX столітті комбінаторика зазнала потужній вплив алгебраїчних методів. Вивчення частково впорядкованих множин, властивостей функції Мебиуса, абстрактних властивостей лінійної залежності, виявлення їхньої ролі при розв’язанні комбінаторних задач сприяли збагаченню комбінаторних методів дослідження й подальшій інтеграції комбінаторики в сучасну математику.
Комбінаторика, як один з розділів дискретної математики, набула важливого значення у зв'язку з використанням її в теорії ймовірностей, математичній логіці, теорії чисел, обчислювальній техніці, кібернетиці.
Бернуллі (Bernoulli) Якоб, 1655 – 1705, математик. На настійну вимогу батька вивчав теологію. Побував у Франції, Бельгії, Англії й в 1682 заснував семінарію експериментальної фізики в Базелі. В 1687 став професором математики Базельського університету, де працював до кінця життя. Зробив істотний вклад у розробку основ диференціального й інтегрального обчислень, аналітичної геометрії, теорії ймовірностей і варіаційного числення. Розв’язав проблему Лейбніца про ізохронну криву, досліджував логарифмічну спіраль, увів полярні координати. В 1685 сформулював, а в 1687–1689 довів закон великих чисел (названий так пізніше Пуассоном). Його головна праця «Мистецтво припущень» (Ars conjectandi), присвячена теорії ймовірностей, була надрукована в 1713 вже після смерті автора.
Ейлер (Euler) Леонард, 1707 – 1783, математик, фізик, механік і астроном. Ще навчаючись у гімназії, слухав в університеті лекції Йоганна Бернуллі (молодшого брата Якоба Бернуллі). Під його керівництвом вивчив в оригіналах праці знаменитих у той час математиків. В 1723 одержав ступінь магістра наук. В 1726 на запрошення Петербурзької АН приїхав у Росію й був призначений ад'юнктом математики. В 1730 очолив кафедру фізики, а в 1733 став академіком математики. Слава Ейлера лунала по всій Європі. Він приймає пропозицію короля Фрідріха II і в 1741 переїжджає в Берлін. Але й у цей час він не порвав зв'язки з Петербургом. В 1746 виходять три томи його статей, присвячених артилерії, у яких він удосконалює формули балістики й надає їм вид, зручний для практичного застосування. Численні відкриття Ейлера в галузі математичного аналізу, зроблені їм за 30 років і надруковані в різних академічних виданнях, були пізніше об'єднані в одній праці "Вступ до аналізу нескінченно малих" (Лозанна, 1748). В 1776 вчений повернувся в Росію. Роботу "Елементи алгебри", що вийшла в 1768, він змушений був диктувати, тому що до цього часу осліп. Робота вийшла російською, німецькою і французькою мовами. Незважаючи на сліпоту, наукова продуктивність Ейлера все зростала. Майже половина його праць створена в останнє десятиліття життя. Він займається гідродинамікою, теорією ймовірностей, теорією чисел та ін. питаннями природознавства. Йому ж належить доведення співвідношення між числом вершин, ребер і граней багатогранника. Майже у всіх областях математики та її застосувань зустрічається ім'я Ейлера: теореми Ейлера. тотожності Ейлера, ейлеровські постійні, кути, функції, інтеграли, формули, рівняння, підстановки й т.д. За кілька днів до смерті займався розрахунком польоту аеростата, що здавався чудом у ту епоху. Вченому належить понад 865 праць з найрізноманітніших і найскладніших питань. Він зробив великий і плідний вплив на розвиток математичної освіти в Російській імперії у 18 ст. Петербурзька математична школа
3
під його керівництвом провела величезну просвітню роботу, створила велику й чудову для свого часу навчальну літературу, виконала ряд цікавих наукових досліджень в галузі математики.
Лейбніц (Ляйбніц, Leibniz) Ґотфрід Вільгельм, 1646 - 1716, німецький філософ,
математик, фізик, мовознавець.
Передбачив принципи сучасної математичної логіки ("Про мистецтво комбінаторики", 1666). Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Незалежно від Ньютона створив диференційне й інтегральне числення і заклав основи двійкової системи числення.
Закінчив Лейпціґський університет, куди вступив в 15 років. У 20 років обрав дипломатичну кар'єру, відмовившись від запропонованої йому посади професора. У 1673 році виготовив механічний калькулятор, зокрема, щоб полегшити працю свого друга астронома Х.Гюйгенса. У машині Лейбніця використовувався принцип зв'язаних кілець підсумовуючої машини Паскаля, але Лейбніц ввів у неї рухомий елемент (прототип каретки настільного калькулятора), що дозволив прискорити повторення операції додавання, необхідне при перемножуванні чисел. Замість коліщат і приводів у машині Лейбніця використовувалися циліндри з нанесеними на них цифрами. Кожен циліндр мав дев'ять рядів виступів або зубців. При цьому перший ряд містив один виступ, другий ряд - два виступи і так аж до дев'ятого ряду, що містив відповідно дев'ять виступів. Циліндри з виступами були рухомими.
Спеціально для своєї машини Лейбніц застосував систему числення, що використовує дві цифри: 0 і 1. Принцип двійкової системи числення Лейбніц пояснював на прикладі коробочки з отворами: відкритий отвір означає 1, закритий - 0. Одиниця позначалася кулею, що випала, нуль - відсутністю кулі. Двійкова система числення Лейбніця знайшла згодом застосування в автоматичних обчислювальних пристроях.
Лейбніц заснував Бранденбурзьке наукове товариство (пізніше - Берлінська АН) і з 1700 був його президентом. На прохання Петра I розробив проекти розвитку освіти і державного керування в Росії.
Леонардо з Пізи, 1170 (або 1180) – 1250, також відомий як Леонардо Пізано,
Леонардо Боначчі або Леонардо Фібоначчі, італійський математик, вважається одним з найталановитіших математиків Середньовіччя. Фібоначчі сьогодні відомий поширенням арабських цифр і індо-арабської системи числення шляхом публікації на початку 13 століття його книги «Liber Abaci» (Книга обчислень). Він також відомий послідовністю, названою на його честь числами Фібоначчі, хоча він і не є її автором , вона була використана в його книзі.
Леонардів батько Вілліам (Guglielmo) мав прозвисько Боначчіо (Bonaccio), тобто добродушний або простий. Відповідно Леонардо одержав прозвисько Фі_Боначчі (Fibonacci), що означало син Боначчіо. Леонардо подорожував разом з батьком, який займався торгівлею з Північною Африкою, там він і дізнався про арабську систему числення.
Усвідомивши, що арабська система простіша і ефективніша за римську, Леонардо їздив по Середземномор’ю, де вчився у кращих арабських математиків. Після повернення у 1202 році у віці 32 років опублікував свою відому книжку. У 1240 році Пізанська Республіка нагородила Фібоначчі призначивши йому персональне утримання.
4
Слайди лекцій
Правилосуми
Об’єктАможнавибрати p способами
Об’єктВможнавибратинезалежновідА - іншимиqспособами
Об’єктАабооб’єктВ - p+q способами
2
ЗадачапроВовочкумаленького
Вовочкаможеїстиманнукашуабовеликою, або маленькоюложкою.
Накухнієдвірізнихвеликих(золотатасрібна) ітри маленьких(інкрустованібурштином, ізумрудами, топазами) ложечки.
СкількомарізнимиспособамиВовочкинаматиможе згодуватийомуманнукашу?
2 великих+ 3 маленьких= 5 способів
3
5
Правилодобутку
Об’єктАможнавибрати p способами
Об’єктВможнавибратинезалежновідА - qспособами
Впорядкованупаруоб’єктівАтаВ |
|
- p·q способами |
4 |
|
ЗадачапроВовочкувеликого
УВовочкиєдвіпарикросівок(Adidas, Reebok) та3 пари джинс(Levi Strauss,Wrangler, Super Rifle).
СкількирізнихваріантівприкідадлядискотекиєуВовочки ?
2 кросовок ×3 джинс= 6 прикідів
5
ЗадачапроВовочкупіжона
УВовочкиєдвікраватки(синяіжовта) татрисорочки (біла, синяізелена).
СкількиіснуєуВовочкирізнихприкідівдлязанятьтаких, щобсорочкаікраваткабулирізногокольору?
2 краватки×3 сорочки= 6 прикідів
6
6

ПринципДіріхле
Середn+1 об’єктаn типів єщонайменше2 об’єкта однаковоготипу
7
ЗадачапроВовочкусоню
УВовочкивгуртожиткувтемнійнижнійшухлядішафи лежатьшкарпетки4 кольорів: білого, чорного,жовтого. синього.
Уразіпідйомуззапізненнямскількишкарпетокне глядячиповиненузятиВовочка, щобутролейбусі можнабулоодягнутишкарпеткиоднаковогокольору?
4 кольори+ 1 = 5шкарпеток
8
Виборки
X ={a1, a2 ,....an }
ai , ai |
, . . . ai |
ai |
X |
1 |
2 |
k |
j |
виборкаоб’ємуk змножиниХ
X={1,2,3,4,5}
<2,3,4> <2,2,3> <4,3,2> <2,3,2>
однаковіякневпорядковані
різніяквпорядковані
9
7

Типивиборок
|
|
порядок |
|
|
|
|
|
|
|
так |
ні |
|
|
|
|
повторен |
та |
впорядкованіз |
невпорядковані |
ня |
к |
повтореннями |
зповтореннями |
|
ні |
впорядковані |
невпорядковані |
|
безповторень |
безповторень |
|
|
|
|
10 |
Розміщення
Кількістьрізних
впорядкованихвиборок
безповторень об’ємуk
зnелементноїмножини
Ak |
|
n |
11 |
Розміщення
Ak = n (n −1) (n −2) ..... (n −k +1) = |
||||||||||||||
|
n |
|
|
|
|
|
|
n! |
|
|||||
|
|
|
|
|
|
= |
|
|
||||||
|
|
|
|
|
|
(n −k)! |
||||||||
|
|
|
|
|
|
|
|
|||||||
1 |
|
2 |
|
3 |
|
|
|
|
k |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n-1 |
|
|
n-2 |
|
|
|
|
n-k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
||
8

Задачапрозбори
ВгрупізNстудентівдляведеннязборівтребаобрати головутасекретаря.
Скількомаспособамиможнацезробити?
Впорядкованапара- (голова; секретар)
А2Nначальникистудентів = N (N-1)
13
Перестановки
Кількістьспособіввпорядкування n-елементноїмножини
Кількістьрізних
впорядкованихвиборок
об’ємуn
зn-елементноїмножини
Pn |
14 |
Перестановки
P |
= |
An = n |
(n −1) (n − |
2) ..... 3 2 1 = |
|||||||||
|
n |
n |
|
|
= n! |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
= n! |
|
|
|
|
|
|
|
|
|
|
|
0! |
|
|
|
|
|
||
|
|
1 |
2 |
3 |
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n-1 |
|
|
n-2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15
9

Задачапроавто
НаталкапідвозитьзуніверситетудометроСашка, МиколуіІвана. Щобвониневідволікалиїївід управліннятранспортнимзасобом, Наталкавсіхїхсадить назаднєсидіння.
Скількиіснуєспособівусістисяхлопцям?
Сашко, Микола, Іван |
Микола, Сашко, Іван |
Іван, Сашко, Микола |
|
1 |
|
3 |
5 |
|
|
|
|
Сашко, Іван, Микола |
Микола, Іван, Сашко |
Іван, Микола, Сашко |
|
2 |
|
4 |
6 |
|
|
|
|
|
Р3 хлопців=3 2 1=6 |
16 |
|
Комбінації
Кількістьрізних
невпорядкованихвиборок об’ємуk
зnелементноїмножини
Ck
n 17
Комбінації
1невпорядкована |
k! впорядкованих |
||||
Cnk Pk = Ank |
Cnk = |
Ank |
|
||
Pk |
|||||
|
|
|
|||
Cnk = |
n! |
|
|
|
|
k!(n −k)! |
|
|
|||
|
|
|
|||
18
10

Задачапроморозиво
Дляодержаннясмачногоморозиваасортітребаузятидва різнихсорти. Скількирізнихтипівасортіможнаприготуватиз шоколадного, полуничного, вершковоготафісташкового
морозива? |
|
|
|
|
||
шоколад+полуниці |
|
|
полуниці+вершки |
|
||
|
|
|
|
|
|
|
шоколад+вершки |
|
|
полуниці+фісташки |
|
||
|
|
|
|
|
|
|
шоколад+ |
|
|
вершки+фісташки |
|
||
фісташки |
|
|
|
|
|
|
|
2 сорти |
= |
4 3 |
= 6 асорті |
||
|
|
|||||
С4 сортів |
|
2 |
19 |
|||
Співвідношеннядля
комбінацій
1 Cnm = Cnn−m , 0 ≤ m ≤ n
2 Cnm = Cnm−−11 + Cnm−1 , 1≤ m ≤ n
3 Cn0 + Cn1 + Cn2 +. . .+Cnn−1 + Cnn = 2n
4 Cn0 − Cn1 + Cn2 −. . .+(−1) n−1 Cnn−1 + (−1) n Cnn = 0
20
Доведенняспіввідношення
Cnm = Cnn−m , 0 ≤ m ≤ n
виборкаоб’ємуm |
|
виборкаоб’ємуn-m |
Cnm |
= |
Cnn−m |
|
|
21 |
11

Доведенняспіввідношення
Cnm = Cnm−−11 +Cnm−1
X = {a1 ,a2 ,...an }
|
виборкизa1 |
Cnm−−11 |
+ |
виборкибезa1 |
+ Cnm−1 |
|
всівиборки |
Cnm |
|
|
22 |
Кількістьпідмножин
A={a1,a2,a3,….an} B A |
|
|
|||
B↔{α1,α2,α3,…..αn} |
|
|
|
||
1 |
ai B |
|
|
|
|
αi = |
ai B |
α1 |
– 2 можливості |
|
|
0 |
α2 |
– 2 |
можливості |
× |
|
|
|
α3 |
– 2 |
можливості |
|
|
|
.............................. |
|
||
|
|
αn – 2 |
можливості |
|
|
2n можливостей
23
Доведенняспіввідношення
Cn0 +Cn1 +Cn2 +...+Cnn−1 +Cnn = 2n
A ={a1,a2 ,...an}
0-елементнихпідмножин |
Cn0 |
|
1-елементнихпідмножин |
Cn1 |
|
………………… |
Cnk |
|
k-елементнихпідмножин |
||
………………… |
2n |
|
|
|
|
Всіпідмножини |
||
24
12

БіномНьютона
n
(a + b) n = ∑Cnk ak bn−k , n > 0
k =0
(a +b)(a +b)....(a +b) = an+an-1 b+….+ak bn-k+…
n разів
ak bn−k |
зk дужокузятоa, |
|
зрешти- n-k дужокузятоb |
||
способіввибратиk дужокзn |
Cnk |
|
|
|
25 |
Доведенняспіввідношення
Cn0 −Cn1 +Cn2 −...+(−1)n Cnn = 0
(1−1)n = Cn0 −Cn1 +....+(−1)n Cnn (1+1)n = Cn0 +Cn1 +....+Cnn
26
ТрикутникПаскаля
1
11
12 1
13 3 1
1 4 6 4 1
коефіцієнтибіномуНьютонапри
коефіцієнтибіномуНьютонапри
коефіцієнтибіномуНьютонапри
коефіцієнтибіномуНьютонапри
коефіцієнтибіномуНьютонапри
n=0
n=1
n=2
n=3
n=4
Cnm−−11 |
Cnm−1 |
+ |
|
Cnm |
27 |
13

Розміщенняз
повтореннями
Кількістьрізних
впорядкованихвиборок
зповтореннями об’ємуk
зnелементноїмножини
Ak |
28 |
n |
|
Розміщенняз
повтореннями
Ank = nk
|
1 |
|
2 |
3 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
29
Перестановкиз
повтореннями
n1 елементів1-готипу
n2 елементів2-готипу
…………………… n1+n2+…+nk=n nk елементівk-готипу
Кількістьрізнихспособіввпорядкування n1 елементів1-готипу,
n2 елементів2-готипу,…. nk елементівk-готипу
Pn(n1,n2,…nk) 30
14

|
Перестановкиз |
|
|
повтореннями |
|
|
ел.1-готипу |
1-йел.1-готипу |
n1 |
ел.1-готипу |
2-йел.1-готипу |
…………... |
…………... |
|
|
{ел.1-готипу |
n1-йел.1-готипу |
|
………….. |
1-йел.k-готипу |
|
ел.k-готипу |
|
nk |
ел.k-готипу |
2-йел.k-готипу |
…………… |
…………... |
|
|
{ |
n -йел.k-готипу |
|
ел.k-готипу |
k |
}n1!
}nk!
Pn (n1, n2 ,...nk ) n1!n2!... nk!= n!
Pn (n1, n2 |
,...nk ) = |
|
n! |
|
|
|
n1!n2 |
!... nk! |
31 |
||||
|
|
|||||
|
|
|
|
|
||
Комбінаціїз
повтореннями
Кількістьрізних
невпрорядкованихвиборок
зповтореннями об’ємуk
зn-елементноїмножини
Cnk
32
Комбінаціїзповтореннями
11...1011..110...0111..11
1-йтип 2-йтип .... n-йтип
1 - k штук, 0 - n-1 штук, усьогозавждиk+n-1 символів
з k+n-1 позицій - k для1 |
Cnk+k −1 |
Cnk = Cnk+k −1 = Cnn+−k1−1
33
15
Скількирозв’язків уцілихневід’ємнихчислах маєрівняння
|
x1 + x2 +.....+xn = k |
xi ≥ 0 |
||||
|
xi - кількістьелементів і-готипу |
|||||
|
|
|
|
|
|
|
|
|
|
Cnk |
|
|
|
|
|
|
|
|
|
34 |
|
Поліноміальна |
|||||
|
теорема |
|
||||
(x1 +x2 +....+xk )n = |
|
|||||
= |
∑Pn (n1 ,....,nk ) x1n1 x2n2 .... xknk |
|||||
n1 |
≥0,...nk ≥0 |
|
|
|
|
|
n1 |
+...+nk =n |
|
|
|
|
|
|
|
|
|
|
|
35 |
|
Поліноміальнатеорема |
|||||
(x1 +...+xk )(x1 +...+xk )...(x1 +...+xk ) |
||||||
x1n1 x2n2 ....xknk |
n1 +n2 +...+nk = n |
ni ≥ 0 |
||||
|
x1 взятозn1 |
дужок |
|
|
||
|
………………. |
|
|
|||
|
xk взятозnk |
дужок |
|
|
||
|
x1x1...x1 x2 x2...x2 |
...xk xk...xk |
|
|||
|
|
|
|
|||
|
n1 |
|
n2 |
nk |
|
|
Pn(n1,n2,….nk) перестановок
36
16

K=2
(x1 + x2 )n = ∑Pn (n1,n2 ) x1n1 x2n2 =
|
|
|
|
|
n1 |
≥0,n2 ≥0 |
|
|
||
|
|
|
|
|
n1 |
+n2 =n |
|
|
|
|
|
n2 |
= n −n1 |
|
|
|
|
|
|||
|
|
|
n |
(n1,n −n1 ) x1n1 x2n−n1 = |
||||||
|
|
|
|
|
= |
∑Pn |
||||
|
|
|
|
|
|
n =0 |
|
|
|
|
P (n |
,n −n )= |
|
1n! |
|
|
= Cn1 |
|
|||
|
|
|
|
|
||||||
|
n |
1 |
1 |
|
n1!(n −n1)! |
n |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
= ∑Cnn1 x1n1 x2n−n1 |
|||||
|
|
|
|
|
n1 =0 |
|
|
37 |
||
Комбінаторнітотожності
таспіввідношення
Література
•Дискретнаяматематика. Учебное пособие, с.39-41
•Ежов, Скороход, ЯдренкоЭлементы комбинаторики, с.38-40.
38
Співвідношеннядля
комбінацій
1 Cnm = Cnn−m , 0 ≤ m ≤ n
2 Cnm = Cnm−−11 + Cnm−1 , 1≤ m ≤ n
3 Cn0 + Cn1 + Cn2 +. . .+Cnn−1 + Cnn = 2n
4 Cn0 − Cn1 + Cn2 −. . .+(−1) n−1 Cnn−1 + (−1) n Cnn = 0
39
17
БіномНьютона
n |
|
(a + b) n = ∑Cnk ak bn−k , n > 0 |
|
k =0 |
|
(a +b)(a +b)....(a +b) |
|
|
|
n разів |
|
зk дужок - a, зn-k - b |
ak bn−k |
k дужокзn |
Cnk |
40
ТрикутникПаскаля
1 |
|
n=0 |
1 1 |
|
n=1 |
1 2 1 |
n=2 |
|
1 3 3 |
1 |
n=3 |
1 4 6 4 1 n=4
Cnm−−11 Cnm−1
|
Cnm |
|
41 |
|
Поліноміальна |
|
теорема |
(x1 +x2 +....+xk )n = |
|
= |
∑Pn (n1 ,....,nk ) x1n1 x2n2 .... xknk |
n1 |
≥0,...nk ≥0 |
n1 |
+...+nk =n |
|
42 |
18

Формулавключень-
виключень
N − предметів
з властивостями α1 ,...α n
N(α i1 , . . . ,α ik ) кількість предметів
з властивостями α i1 , . . . ,α ik
N(α1′,...,α′n ) - кількість
предметів, що не мають жодної властивості α1 ,..,αn
43
Формулавключень-
виключень
N (α1′,...,α′n ) = N − ∑N (αi ) + ∑N (αi1 ,αi2 )+... |
|
|||
|
|
|
i |
|
+(−1)s |
∑N (αi1 ,...,αis )+...+(−1)n N (α1 ,...,αn ) |
|
||
|
i1 <i2 <...<is |
|
|
|
|
a з властивостями αj1 ,...,α jr |
|
||
|
s≤r |
в |
∑N(αi1 ,...,αis ) Crs разів |
|
|
|
i1 |
<i2 <...<is |
|
|
1− Cr1 + Cr2 −...+(−1) r Crr = 0 |
|
||
s>r |
|
0 разів |
44 |
|
Формулавкл-виклдляпідмножин
X,Xi X,1 ≤ i ≤ n
N(Xi) - кількістьелементіввXi
αi (x) x Xi N(X1 X2 ... Xn ) =
N(X) −∑N(Xi ) +...+(−1)n N(X1 ∩ X2 ∩...∩ Xn )
i |
|
|
|
|
|
|
|
N(X1 X2 |
... Xn ) = |
|
|||||
= N(X) − N( |
X1 |
X2 ... Xn |
) = |
|
|||
= ∑N(Xi ) − |
∑N(Xi1 ∩ Xi2 ) +.... |
|
|||||
i |
n |
|
|
|
|
||
....+(−1) |
N(X1 ∩...∩ Xn ) |
45 |
|||||
|
|
||||||
|
|
|
|
|
|
||
19
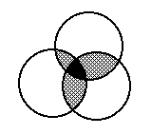
Формулавключень-виключеньдля3- x множин
B
A C
N ( A B C) = N ( A) + N (B) + N (C) −
−N ( A ∩ B) − N ( A ∩ C) − N (B ∩ C) +
+N ( A∩ B∩ C)
46
Прикладвключень-виключеньдля3- x множин
100-хлопців; 30-самбо; 50-карате; 40-конфу
15-самбо+карате; 10-самбо+конфу; 20-карате+конфу; 7-самбо+карате+конфу
слабаки=100-30-50-40+15+10+20-7=18
47
ФункціяЕйлера
ϕ(n) - кількістьвзаємнопростихзn таменшихзаn натуральнихчисел
n = p1n1 p2n2 ... pknk pi |
− прості |
|||||
α1,α2 ,...,αk |
:αi (m) pi | m, m ≤ n |
|||||
N(αi ,...,αi |
) = |
|
n |
|
||
pi |
... pi |
|||||
1 |
s |
|
||||
|
|
|
|
|||
|
|
|
1 |
s |
||
48
20
N(αi |
,...,αi |
) = |
|
n |
|
pi |
... pi |
||||
1 |
s |
|
|||
|
|
|
|||
|
|
|
1 |
s |
k враховуют ься в N(αi1 ,...,αis )
k ≤ n, pi1 | k, pi2 | k, ...pis | k m = pi1 pi2 .... pis
k ≤ n, m| k
m, 2m, 3m,……... n
49
ФункціяЕйлера
ϕ(n) = N (α1′,... ,α′k )
|
ϕ(n) = n −∑ |
n |
|
+∑ |
|
n |
|
|
|
|
−... |
||||||||||
|
p p |
|
|
|
|
||||||||||||||||
|
|
|
i |
|
p |
|
|
|
i |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
||
|
|
|
+(−1)n |
|
|
n |
|
|
|
|
|
= |
|
||||||||
|
|
|
p p |
...p |
k |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|||
|
= n(1− |
1 |
)(1− |
|
1 |
)...(1− |
|
|
1 |
) |
|
||||||||||
|
|
p |
|
|
|
p |
|
||||||||||||||
|
|
|
p |
|
|
|
|
2 |
|
|
|
|
|
k |
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Cr−1 |
+ Cr−1 +...+Cr−1 |
= Cr |
|
|
|
|
||||||||||||||
|
n−1 |
n−2 |
|
|
|
|
|
r−1 |
|
|
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
{a1 , a2 ,... , an } |
|
{ai1 |
,... , air } |
|
|
Cnr |
|
|
|||||||||||||
Tk − |
min is = k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
N (T ) = Cr−1 |
1 ≤ k ≤ n − r +1 |
|
|
|
|
|||||||||||||||
|
k |
n−k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∑N (Tk ) = Cnr
51
21

|
|
Cr−1 |
+ Cr−1 +...+Cr−1 |
= Cr |
|
|||||||||
|
|
|
n−1 |
|
|
n−2 |
r−1 |
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
(r,n-r) Всьогошляхів |
Cnr |
|||
|
|
|
|
|
|
|
|
|
|
Bk |
першіk кроківвгору |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
N(B ) = Cr −1 |
−1 |
0 ≤ k |
≤ n −r |
||
|
|
|
|
|
|
|
|
k |
n−k |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0,0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−r |
|
|
|
|
|
|
|
|
|
|
∑N(Bk ) = ∑Cnr−−1k−1 = Cnr |
|||||||
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
Cn0 Cmk + Cn1 Cmk −1 +...+Cnk Cm0 = Cnk+m
Cnk+m |
− |
{ai |
,...,ai } |
{a1,...,an} {an+1,...an+m} |
|
|
1 |
k |
|
Vi - виборкизрівноi елементамиулівіймножині
N(Vi ) = Cni Cmk−i0 ≤ i ≤ k
k |
|
∑N(Vi ) = ∑Cni Cmk−i = Cnk+m |
|
i=0 |
53 |
Cn0 Cmk + Cn1 Cmk −1 +. . .+Cnk Cm0 = Cnk+m
(1+ x) n (1+ x) m = (1+ x) n+m
xi |
xk −i |
xk 0 ≤ i ≤ k |
Cni |
Cmk −i |
Cnk+m |
k |
|
∑Cni Cmk −i = Cnk+m |
|
i= |
0 |
54
22

Рекурентні
співвідношення
Література
•Дискретнаяматематика. Учебноепособие,
стр.43-55.
55
КроликиФібоначчі
Раміна
Плачідо
|
|
|
|
56 |
|
|
А ж |
|
|
|
|
ч |
|
|
|
А ж |
|
B ж |
1-ймісяць |
|
ч |
|
ч |
|
А ж |
|
C ж |
B |
ж |
ч |
|
ч |
ч |
2-ймісяць |
|
|
|||
А ж |
D ж |
C ж |
3-ймісяць |
|
B ж |
E ж |
|||
ч |
ч |
ч |
ч |
ч |
4-ймісяць
1,2,3,5,8,13,21,34,...
57
23

Кролики(числа) Фібоначчі
F(n) - кількістьпаркроликів
наn-мумісяці
F(0)=1, F(1)=2
F(n-1) - кількістьстаттєвозрілих
парнаn-мумісяці
F(n+1)= F(n)+F(n-1)
58
Рекурентні
співвідношення
f(n + k) = a1 f (n + k −1) + a2 f (n + k − 2)+. . .
(1)....+ak−1 f (n +1) + ak f (n)
лінійне, однорідне, k-гопорядку f(n) - розв’язок
(2)λk = a1λk −1 + a2 λk −2 +. . .+ak −1λ + ak
Характеристичнерівняннядля рекурентногоспіввідношення(1)
59
Характеристичнерівняння
f (n + k) = a1 f (n + k −1) + a2 f (n + k − 2)+. . .
....+ak−1 f (n +1) + ak f (n)
f(n)=λn
λn+k=a1 λn+k-1+a2 λn+k-2+……+ak λn
λk=a1 λk-1+a2 λk-2+……+ak
60
24

Лема1
Нехай f1 (n), f 2 (n), . . . , f m (n) розв’язки
рекурентногоспіввідношення(1), c1 , c2 , . . . , cm довільніконстанти
тоді
f (n) = c1 f1 (n)+. . .+cm f m (n)
такожрозв’язокспіввідношення(1)
Лінійнакомбінаціярозв’язківрекурентного співвідношеннятакожєрозв’язком 61
f1(n+k)=a1f1(n+k-1)+…..+akf1(n) |
×c1 |
+ f2(n+k)=a1f2(n+k-1)+…..+akf2(n) |
×c2 |
fm(n+k)=a1fm(n+k-1)+…..+akfm(n) |
×cm |
c1f1(n+k)+….+cmfm(n+k)=a1(c1f1(n+k-1)+..+cmfm(n+k-1))+..
..+ak( c1f1(n)+….+cmfm(n))
f(n)=c1f1(n)+….+cmfm(n)
f(n+k)=a1f(n+k-1)+…..+akf(n) 62
Лема2
λ - коріньрівняння(2),тоді f (n) = λn - розв’язок(1)
f(n + k) = λ n+k = a1λ n+k −1 +. . .+ak λ n
λk = a1λk −1 + a2λk −2 +...+ak
63
25

Теорема3 пропростікорені(2)
λ1 ,λ2 , . . . ,λk простікореніхар.рівняння(2)
(λ − λ1 )(λ − λ2 )...(λ − λk ) = 0 λi ≠ λ j
тоді
довільнийрозв’язокf(n) можебутипредставленийяк
f (n) = c1λn1 +. . .+ck λnk |
, де |
||
c1,c2 ,...,ck |
деякіконстанти 64 |
||
λi ≠ 0 |
ak |
= 0 |
|
f (0), f (1), . . . . . , f (k −1)
c1 +c2 +. . .+ck |
= f (0) |
|||
|
|
+c2 λ2 +. . .+ck λk = f (1) |
||
c1λ1 |
||||
|
|
|
. . . . . . . . . . . . . . . . . |
|
|
|
|
||
|
|
|
|
|
|
k −1 |
k −1 |
= f (k −1) |
|
c1λ1 |
|
+. . .+ck λk |
||
65
1 |
1 |
... |
1 |
|
|
|
|||||
λ 1 |
λ 2 |
... |
λ k |
= |
|
... |
... ... ... |
||||
|
|||||
λk1−1 |
λk2−1 |
... |
λkk−1 |
|
|
= ∏(λ i − λ j )
i> j
66
26
Співвідношеннядлякроликів
F(n+1)=F(n)+F(n-1), F(0)=1, F(1)=2
λ2 = λ +1 λ 1 = 1+2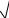 5 , λ 2 = 1−2
5 , λ 2 = 1−2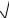 5
5
F (n) = c1 1+2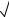 5 n + c2 1−2
5 n + c2 1−2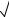 5 n
5 n
67
|
|
|
c1 |
|
|
|
1+ |
c |
|
|
|
|
1 |
|
2 |
|
|
||
+
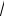 5 +
5 +
|
|
c2 |
|
|
= |
1 |
c2 |
1− |
5 |
= |
2 |
||
|
2 |
|
|
|||
|
|
|
|
|
|
c1 = 21 1+ 355 , c2 = 21 1− 355
|
|
|
3 |
|
|
1+ |
|
|
n |
|
|
|
3 |
|
|
1− |
|
|
n |
||
1+ |
5 |
5 |
+ |
1− |
5 |
5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
F (n) = |
|
|
5 |
2 |
|
|
|
|
|
|
5 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68
Теорема4 прократнікорені(2)
λ 1 −корінь кратності k1 ,...,λ s − ks k1 + k2 +. . .+ks = k
(2) (λ − λ 1)k1 ....(λ − λ s )ks = 0
тоді
1.λ nj , nλ nj , n2 λn j , . . . , nk j −1λ nj
j=1,...s, розв’язкиспіввідношення(1)
69
27

2. Загальнийрозв’язок(1) f (n) =
= ∑s (Cj,1 + Cj,2 n+...+Cj,kj |
nkj −1)λ nj |
j=1 |
|
Cj,m , j = 1,...s, m = 1,...kj |
− |
- довільніконстанти
70
Неоднорідне... співвідношення
(3) f (n + k) = a1 f (n + k −1)+. . .+ak f (n) + q(n)
Теорема5
f*(n) - окремийрозв’язок(3)
F(n) - загальнийрозв’язоквідповідного(1)
тоді
Загальнийрозв’язок(3) можебутиодержано, якf(n)=f*(n)+F(n)
|
|
|
|
|
|
71 |
1. Нехайf(n) – розв'язок, знайдемоF(n), що: |
|
|||||
F(n) - розвязокоднорідногота |
|
|||||
f(n)=f*(n)+F(n) |
k |
|
||||
- |
f (n +k) = ∑ai f (n +k −i) +q(n) |
|
||||
|
k |
|
||||
|
|
i=1 |
|
|||
|
f *(n + k) = ∑ai f *(n + k − i) + q(n) |
|
||||
|
|
i=1 |
|
|||
|
|
|
|
|
|
|
|
f (n +k) − f *(n +k) = |
|
||||
|
k |
|
|
|
|
|
|
= ∑ai (f (n +k −i) − f *(n +k −i)) |
|
||||
|
i=1 |
|
|
|
|
|
|
|
k |
F (n) = f (n) − f *(n) |
|
|
|
|
|
|
|
|
|
|
F (n +k) = ∑ai F (n +k −i) |
72 |
|||||
i=1
28

2. НехайF(n) – розв'язокоднорідного, доведемо, що
|
f(n)=f*(n)+F(n) будерозв'язкомнеоднорідного |
|
|
k |
|
|
f *(n +k) = ∑ai f *(n +k −i) +q(n) |
|
+ |
i=1 |
|
k |
||
|
||
|
F(n +k) = ∑ai F(n +k −i) |
|
|
i=1 |
f *(n +k) + F(n +k) =
k |
|
|
|
|
= ∑ai (f *(n +k −i) + F(n +k −i))+q(n) |
||||
i=1 |
|
|
|
|
k |
f (n) = f *(n) + F(n) |
|
||
|
|
|
||
|
|
|
|
|
f (n |
+k) = ∑ai f (n +k −i) +q(n) |
73 |
||
i=1
Лема6. q(n)=p·bn
Якщоb неєрозв’язком(2), тоокремийрозв’язок(3)
приq(n)=p•bn
можебутизнайденийувиді f*(n)=c·bn
k
c bn+k = ∑ai c bn+k −i + p bn
i=1
74
|
k |
||
c bk = c ∑ai bk−i + p |
|||
|
i=1 |
||
c = |
p |
||
|
|
||
k |
|||
|
|||
|
bk − ∑ai bk −i |
||
|
i=1 |
||
75
29

Твірніфункції
Література
•ВиленкинКомбинаторика, стр.182-216
•Дискретнаяматематика. Учебноепособие,
стр.50-57.
•ХоллМ. Комбинаторика, стр.33-44.
76
Твірніфункції
a0 , a1 , a2 , . . . , an , . . .
∞
f (x) = ∑ai xi
i=0
n
f (x) = lim∑ai xi
n→∞ i=0
111,,, . . .1, . . . f (x) = 1+ x + x2 +. . . = 1−1x
77
an = Cpn f (x) = (1+ x) p
k1x1 + k2 x2 +. . .+kr xr = n
an - кількість невід′ємних рішень
f (x) = (1+ xk1 + x2k1 +. . .). . .(1+ xkr + x2kr +. . .)=
= (1− xk1 ). 1. .(1− xkr )
78
30
Твірнафункціякроликів
(1) F (n + 2) = F (n +1) + F (n), |
F (0) = 1, F (1) = 2 |
|
|
∞ |
∞ |
|
f (x) = ∑F (n) xn |
∑ (1) xn+2 |
|
n=0 |
n=0 |
∞ |
∞ |
∞ |
∑F (n + 2) xn+2 = ∑F (n +1) xn+2 + ∑F (n) xn+2 |
||
n=0 |
n=0 |
n=0 |
79
f (x) − F (0) − F (1) x = x ( f (x) − F (0)) + x2 f (x)
f (x) − xf (x) − x2 f (x) = 1+ 2x − x
f (x) = |
1+ x |
|
1− x − x2 |
||
|
80
Твірніф-їдлярек.співвід-нь
g(n + k) = a1g(n + k −1)+. . .+ak g(n)
∞ |
∞ |
f (x) = ∑g(n) xn ∑ ........ xn+k |
|
n=0 |
n=0 |
∞ |
∞ |
∑g(n + k) xn+k = ∑a1 g(n + k −1) xn+k +. . . |
|
n=0 |
n=0 |
∞
. . . .+∑ak g(n) xn+k
n=0
81
31

f (x) = |
g(0) + (g(1) − a1g(0))x+... |
...... |
||||||
1− a x − a |
2 |
x2 |
−...a |
k |
xk |
|
||
|
1 |
|
|
|
|
|
||
......+(g(k −1) −a1g(k −2) −...−ak−1g(0)) xk−1
82
Теоремапролінійну
комбінацію
{a1i } f 1 (x)
................. C1 , . . . Ck − константи
{aik } f k (x)
тоді
{C1a1i +. . .+Ck aik } C1 f 1 (x)+. . .+Ck f k (x)
83
∞
∑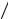 C1 ai1 +... +Ck aik
C1 ai1 +... +Ck aik 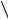 xi =
xi =
i=0
∞ |
∞ |
= C1 ∑ai1 |
xi +... +Ck ∑aik xi = |
i=0 |
i=0 |
= C1 f 1(x)+...+Ck f k (x)
84
32
