Lysenko_physics_lek_2[1]
.pdf
dP = |
|
Ψ |
|
2 dV = Ψ*ΨdV |
. |
(84.2) |
|
|
|||||
|
|
|
|
|
|
|
Співвідношення визначає фізичну сутність хвильової функції: квадрат модуля хвильової
функції в деякій точці простору є густиною ймовірності знаходження частинки в цій точці простору ( dP / dV = Ψ 2 ).
Виходячи з фізичного змісту квадрата модуля хвильової функції можемо знайти, що інтеграл від виразу (84.2), узятий в усьому просторі, повинен дорівнювати одиниці:
òΨ*ΨdV = 1. |
(84.3) |
Дійсно, цей інтеграл дає ймовірність того, що частинка знаходиться в одній із точок простору, що є подією достовірною. Відомо, що ймовірність достовірної події дорівнює одиниці. Співвідношення (84.3) називають умовою нормування.
3 З інтерпретації Борна (84.2) випливає, що квадрат модуля хвильової функції є густиною імовірності (імовірністю, віднесеною до одиниці об'єму) знаходження частинки у відповідному місці простору. З цього випливають такі властивості хвильової функції. Псі-функція повинна:
1)бути однозначною, неперервною й скінченною (за винятком, може бути, особливих точок);
2)мати однозначну, неперервну та скінченну похідну;
3)інтеграл òΨ*ΨdV , узятий по всьому простору, повинен бути скінченним.
Сукупність перелічених вище вимог називають стандартними умовами для хвильової функції.
§ 85 Загальне й стаціонарне рівняння Шредінгера [6]
1 Розвиваючи ідеї де Бройля про хвильові властивості речовини, Шредінгер отримав у 1926 р. рівняння для визначення хвильової функції. Воно дозволяє знайти хвильові функції частинок, які рухаються в різних силових полях. Рівняння виглядає так:
|
|
h2 |
∂ψ |
|
|
|
|
|
− |
|
ΔΨ +UΨ = ih |
∂t |
. |
(85.1) |
|
2m |
|||||||
Тут m – маса частинки; i – уявна одиниця; U – |
потенціальна енергія частинки; |
– |
|||||
оператор Лапласа, результат дії якого на деяку функцію є сумою других частинних похідних за координатами:
ΔΨ = |
∂2 |
Ψ |
+ |
∂2 |
Ψ |
+ |
∂2 |
Ψ |
. |
(85.2) |
|
∂x2 |
∂y2 |
∂z2 |
|||||||||
|
|
|
|
|
|||||||
Рівняння (85.1) називають загальним рівнянням Шредінгера. З рівняння (85.1) випливає, що вигляд хвильової функції визначається потенціальною енергією U , тобто в остаточному підсумку характером сил, що діють на частинку.
Рівняння Шредінгера є основним рівнянням нерелятивістської квантової механіки. Воно не може бути доведене з інших співвідношень. Його варто розглядати як вихідне основне припущення, справедливість якого доводиться тим, що всі наслідки, які випливають із нього, точно узгоджуються з дослідними фактами.
Шредінгер установив своє рівняння, виходячи з оптико-механічної аналогії. Ця аналогія полягає в подібності рівнянь, які описують хід світлових променів, з рівняннями, що визначають траєкторії частинок у класичній механіці.
Пояснимо, як можна прийти до загального рівняння Шредінгера. Для простоти обмежимося одновимірним випадком. Розглянемо частинку, яка вільно рухається.
171
- |
h2 |
exp[- i(E / h)t] Dy +Uy exp[-i(E / h)t] = ih[-i(E / h)]y exp[- i(E / h)t] . |
|
2m |
|||
|
|
Скоротивши на загальний множник exp[- i(E / h)t] , прийдемо до диференціального рівняння, що визначає функцію ψ :
- |
h2 |
Dy +Uy = Ey |
. |
(85.5) |
|
2m |
|||||
|
|
|
|
Рівняння (85.5) називається рівнянням Шредінгера для стаціонарних станів
(стаціонарне рівняння Шредінгера) . Надалі ми будемо мати справу тільки із цим рівнянням і для стислості будемо називати його просто рівнянням Шредінгера. Рівняння (85.5) часто пишуть у вигляді
Dy + |
2m |
(E -U )y = 0. |
(85.6) |
|
|
||||
|
h |
2 |
|
|
|
|
|
|
|
У випадку стаціонарного силового поля хвильова функція має вигляд (85.4). Тоді
Y*Y = exp[i(E / h)t]y* ×exp[-i(E / h)t]y = y*y .
Таким чином, густина імовірності дорівнює y*y й, отже, від часу не залежить. Саме тому
стани, які описуються хвильовими функціями вигляду (85.4), називають стаціонарними.
3 У класичній механіці стан частинки (матеріальної точки) визначається завданням положення і швидкості (або імпульсу) частинки. Якщо є відомим стан у початковий момент часу й силове поле, у якому знаходиться частинка, то, розв’язавши рівняння Ньютона, можна знайти положення й швидкість частинки у будь-який наступний момент часу. У цьому полягає сутність причинності в класичній механіці.
Уквантовій механіці класичне поняття стану позбавлене змісту, тому що координата
йшвидкість частинки принципово не можуть мати одночасно певних значень. Тому класичне поняття причинності також не можна застосовувати у квантовій теорії. Стан частинки задається у квантовій механіці хвильовою функцією. Якщо відомі хвильова функція в початковий момент часу й силове поле, у якому рухається частинка, то, розв’язавши рівняння Шредінгера, можна знайти хвильову функцію в наступні моменти часу. У цьому полягає сутність причинності у квантовій механіці. Таким чином, квантова механіка не скасувала принцип причинності. Вона лише надала йому форму, яка відповідає дійсній природі речей.
§ 86 Рівняння Шредінгера та квантування енергії [6]
1 Квантування енергії виникає тому, що на хвильові функції ψ , які є розв’язками рівняння Шредінгера
- |
h2 |
Dy +Uy = Ey , |
(86.1) |
|
2m |
||||
|
|
|
накладаються певні обмеження – стандартні умови для хвильової функції. При цих обмеженнях рівняння (86.1) має розв’язки, у загальному випадку, не при всіх, а тільки при вибраних значеннях параметра E ( E визначає енергію частинки). Тут маємо випадок,
аналогічний до того, що має місце в задачі про вільні коливання струни із закріпленими кінцями. Через закріпленість кінців ці коливання є стоячими хвилями з такими вибраними частотами, що на довжині струни вкладається ціле число напівхвиль.
Стандартні умови для хвильової функції, що накладаються на розв’язки рівняння Шредінгера, полягають у тому, що хвильова функція y(x, y, z) і її перші просторові похідні повинні бути скінченними, однозначними й неперервними, інтеграл від y(x, y, z) по усьому
173
простору повинен бути скінченним. Вибрані значення параметра E , для яких рівняння Шредінгера має розв’язки, що задовольняють стандартні умови, називаються власними значеннями величини E для диференціального рівняння (86.1), а відповідні їм розв’язки – власними функціями того самого рівняння. Власні значення E і беруть за можливі значення енергії у стаціонарних станах. Власні значення енергії E можуть бути
дискретними, а можуть неперервно заповнювати скінченний або нескінченний інтервал. У першому випадку говорять, що енергетичний спектр дискретний, а в другому – неперервний.
Таким чином, квантування енергії випливає з основних положень квантової механіки без будь-яких додаткових припущень.
§ 87 Частинка в одновимірній потенціальній ямі. Енергія і хвильова функція частинки в потенціальній ямі [6]
1 У нерелятивістській квантовій механіці основним принципом є рівняння Шредінгера. Пошук розв’язків цього рівняння, які задовольняють стандартні умови, приводить до дискретності енергетичних рівнів. Продемонструємо це на прикладі задачі про частинку, яка знаходиться в одновимірній нескінченно глибокій потенціальній ямі.
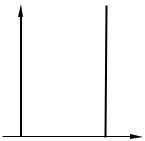
Знайдемо власні значення енергії й відповідні їм власні функції для частинки, що знаходиться в нескінченно глибокій одновимірній потенціальній ямі. Припустимо, що частинка може рухатися тільки уздовж осі X . Нехай рух обмежений непроникними для частинки стінками з такими координатами: x = 0 і x = l . Потенціальна енергія U має в цьому випадку такий вигляд (рис. 87.1а): вона дорівнює нулю при 0 ≤ x ≤ l й перетворюється у нескінченність при x < 0 й x > l . Для розв’язання задачі використаємо стаціонарне рівняння Шредінгера
|
|
ψ + |
2m |
(E −U )ψ = 0. |
|
(87.1) |
|||||
|
|
|
|
||||||||
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
n = 4 |
|
E4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
U = ∞ |
|
|
|
U = ∞ |
|
|
n = 3 |
|
|||
|
|
|
|
|
|
E3 |
|||||
|
|
|
|
|
n = 2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
l |
|
|
x |
|
|
|
01 |
|||
|
|
a |
|
|
|
|
|
б |
|
|
|
Рисунок 87.1: а – нескінченно глибока потенціальна яма; б – схема рівнів енергії частинки, що знаходиться в такій ямі
2 Оскільки хвильова функція залежить тільки від координати x , то рівняння (87.1) спрощується:
∂2ψ |
+ 2m (E −U )ψ = 0 . |
(87.2) |
∂x2 |
h2 |
|
За межі потенціальної ями частинка потрапити не може (там потенціальна енергія дорівнює нескінченності U = ∞ ). Тому ймовірність виявлення частинки за межами ями дорівнює нулю. Відповідно й функція ψ за межами ями дорівнює нулю. З умови
неперервності випливає, що ψ повинна дорівнювати нулю й на межах ями, тобто |
|
ψ(0)= ψ(l)= 0. |
(87.3) |
174
Це і є одна із стандартних умов, яку повинен задовольняти розв’язок рівняння (87.2). В області, де ψ не дорівнює тотожно нулю, рівняння (87.2) має вигляд
¶2y |
+ |
2m |
Ey = 0 |
(87.4) |
|
¶x2 |
h2 |
||||
|
|
|
|||
(у цій області U = 0 ). Увівши позначення |
|
|
|
|
|
k2 = 2m E , |
(87.5) |
||||
|
|
h |
2 |
|
|
|
|
|
|
||
прийдемо до рівняння |
|
|
|
|
|
y¢¢ + k 2y = 0 , |
|
||||
яке в теорії коливань називають диференціальним рівнянням |
гармонічних коливань. |
||||
Розв’язок такого рівняння має вигляд |
|
|
|
|
|
y(x)= Asin(kx + a) |
(87.6) |
||||
(у цьому випадку зручніше взяти синус замість косинуса). Умови (87.3) можна задовольнити
відповідним вибором сталих k |
і α . Насамперед з умови y(0)= 0 отримуємо |
|
|
y(0)= Asin a = 0 , |
|
звідки випливає, що α повинна дорівнювати нулю. Також повинна виконуватися умова |
||
|
y(l)= Asin(kl)= 0 , |
|
що можливо лише у випадку, коли |
|
|
|
kl = ±np (n =1, 2, 3, ...) |
(87.7) |
( n = 0 не беремо до уваги, |
оскільки при цьому виходить, що ψ = 0 |
– частинка у |
потенціальній ямі відсутня).
Виключивши k з рівнянь (87.5) і (87.7), знайдемо власні значення енергії частинки:
E = En = |
p2h2 |
n2 |
(n =1, 2, 3, ...) |
. |
(87.8) |
|
2ml2 |
||||||
|
|
|
|
|
Спектр енергії виявився дискретним. На рис. 87.1б зображена схема енергетичних рівнів. Відповідно до формули (87.8) мінімальна енергія, яку може мати частинка, що
знаходиться в потенціальній ямі, відмінна від нуля. Цей результат обумовлений хвильовими властивостями частинки й може бути отриманий зі співвідношення невизначеностей.
3 Далі знайдемо власну хвильову функцію рівняння Шредінгера. Підставивши в (87.6) значення k , яке отримали з умови (87.7), знайдемо власні хвильові функції:
|
|
|
|
|
|
y = yn (x)= Asin |
npx |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(нагадаємо, що α = 0 ). Для знаходження коефіцієнта |
A використаємо умову нормування, |
|||||||||||||||||||
яку у цьому випадку запишемо так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
l |
npx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 òsin2 |
dx =1. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нескладно отримати, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
l |
|
2 npx |
|
l |
1- cos(2npx / l) |
æ x |
|
sin(2npx / l)ö |
|
l |
|
l |
|
|||||||
|
|
|
|
|
|
|||||||||||||||
ò |
|
|
|
|
ò |
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
sin |
|
l |
dx = |
|
2 |
dx = ç |
2 |
|
- |
2 |
×(2np/ l) |
÷ |
|
|
= |
2 |
. |
||
0 |
|
|
|
0 |
|
è |
|
|
ø |
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
175
Звідси A2 ×l / 2 =1, або A = |
2 / l . Таким чином, власні функції частинки в потенціальній |
||||
ямі мають вигляд |
|
|
|
|
|
|
yn (x)= |
2 sin |
npx |
(n =1, 2, 3, ...). |
(87.9) |
|
|
l |
l |
|
|
ψ |
n = 4 |
|
y y |
|
n = 4 |
|
|
|
|||
|
n = 3 |
|
|
|
n = 3 |
|
|
|
|
|
|
|
n = 2 |
|
|
|
n = 2 |
|
|
|
|
|
|
|
|
|
|
|
n =1 |
|
n =1 |
|
|
|
|
0 |
|
l x |
|
0 |
l x |
a |
|
|
|
б |
|
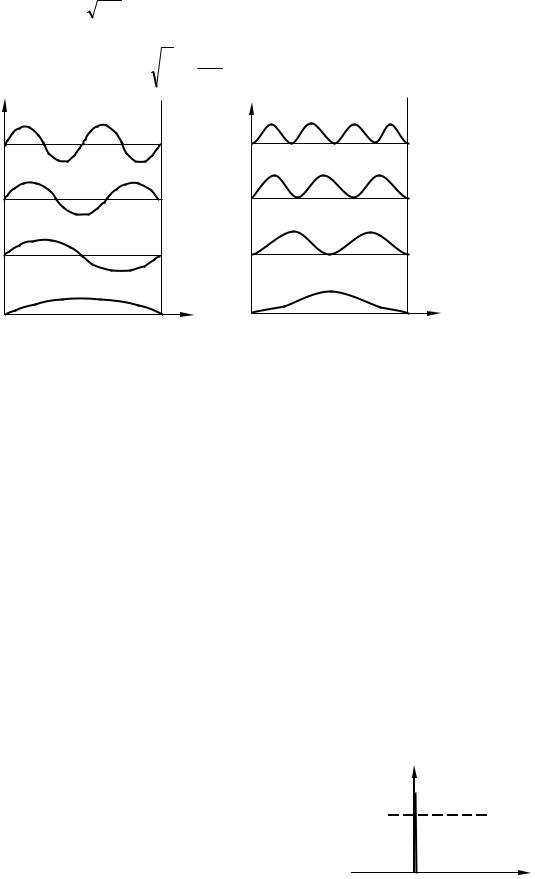
Рисунок 87.2: а – графіки власні функції частинки, що знаходиться в потенціальній ямі, яка зображена на рис. 87.1а; б – густина ймовірності знаходження частинки в точках з різними значеннями координати x
Графіки власних функцій зображені на рис. 87.2а. На рис. 87.2б подана густина ймовірності виявлення частинки на різних відстанях від стінок ями, що дорівнює y*y . Із
графіків, наприклад, випливає, що в стані із n = 2 частинка не може бути виявлена всередині ями й разом з цим однаково часто буває як у лівій, так і в правій половині ями. Така поведінка частинки є несумісною з класичними уявленнями про траєкторії. Відзначимо, що відповідно до класичних уявлень усі положення частинки в ямі мають однакову ймовірність.
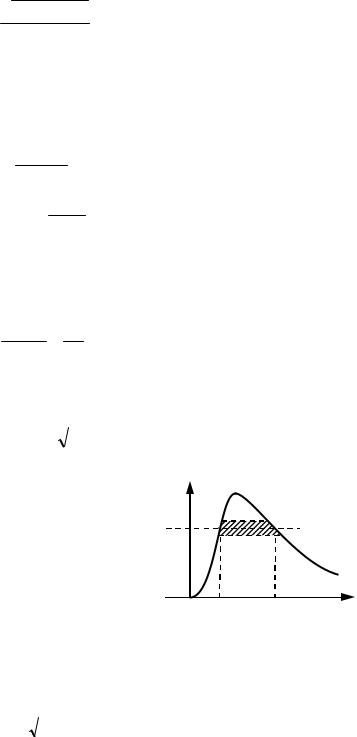
§ 88 Тунельний ефект. Коефіцієнт проходження [3] 1 Нехай частинка, яка рухається зліва направо, зустрічає на своєму шляху
потенціальний бар'єр висотою U0 й шириною l |
(рис. 88.1). За класичними уявленнями |
|||||||||
частинка повинна вести себе так. Якщо енергія частинки більша за висоту бар'єра ( E >U0 ), |
||||||||||
частинка безперешкодно проходить над бар'єром (на ділянці |
0 ≤ x ≤ l |
лише зменшується |
||||||||
швидкість частинки, але потім при x > l знову набуде початкового значення). Якщо ж |
E |
|||||||||
менше U0 (як зображено |
на рисунку), то частинка відбивається від бар'єра й летить |
у |
||||||||
зворотній бік; крізь бар'єр частинка проникнути не може. |
|
|
|
|
|
|
||||
Зовсім інакше виглядає поведінка частинки з точки зору |
|
U (x) |
|
|
||||||
до квантової механіки. По-перше, навіть при E >U0 |
є відмінна |
|
|
|
||||||
|
U0 |
|
|
|
||||||
від нуля ймовірність того, що частинка відіб'ється від бар'єра й |
|
|
|
|
||||||
|
E |
|
|
|
|
|||||
полетить у зворотній бік. По-друге, при E <U0 |
є відмінна від |
|
|
|
|
|
||||
|
I |
|
II |
III |
|
|||||
нуля ймовірність того, що частинка проникне «крізь» бар'єр і |
|
|
|
|||||||
опиниться в області, де |
x > l . Така поведінка |
є цілком |
|
|
|
|
|
x |
||
неможливою з класичної точки зору. Ця |
поведінка |
|
|
0 |
l |
|||||
мікрочастинки |
випливає |
безпосередньо |
з |
рівняння |
Рисунок 88.1 |
|
|
|||
Шредінгера. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 Розглянемо випадок E <U0 . Рівняння Шредінгера має вигляд
176
|
βA eβl |
−βB |
e−βl = iaA eiαl . |
|
|||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
Розділимо всі рівняння на A1 й введемо позначення: |
|
|
|
|
|
|
|
||||||||||||||||||||
b = |
B1 |
, a |
2 |
= |
|
A2 |
, b = |
B2 |
|
, a |
3 |
= |
A3 |
, |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
A1 |
|
|
|
|
A1 |
|
|
|
2 |
|
|
A1 |
|
|
A1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а також |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n = |
= |
|
|
|
U0 − E |
. |
|
|
|
(88.8) |
|||||||||||||
|
|
|
|
α |
|
|
|
|
|
|
|
E |
|
|
|
|
|
||||||||||
Тоді рівняння (88.7) наберуть вигляду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1+ b1 = a2 + b2 , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
a |
eβl |
+ b e−βl |
|
= a eiαl , |
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
(88.9) |
||||||
|
i − ib1 = na2 − nb2 , |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
na |
eβl − nb e−βl = ia |
eiαl . |
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
Відношення квадратів модулів амплітуд відбитої й падаючої хвилі |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
R = |
|
1 |
|
|
|
= |
b |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
визначає ймовірність відбиття частинки від потенціального бар'єра й називається
коефіцієнтом відбиття.
Відношення квадратів модулів амплітуд хвилі, що пройшла, й падаючої хвилі
|
|
A |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
D = |
|
3 |
|
|
|
|
= |
a3 |
|
(88.10) |
|
A |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
визначає ймовірність проходження частинки через бар'єр і називається коефіцієнтом проходження (або коефіцієнтом прозорості).
Нас буде цікавити тільки проходження частинок через бар'єр, і ми обмежимося знаходженням величини D . Слід зазначити, знайшовши D , легко знайти R , оскільки ці коефіцієнти пов'язані очевидним співвідношенням R + D =1.
Помножимо перше з рівнянь (88.9) на i й складемо з третім. У результаті отримаємо
2i = (n + i)a2 − (n − i)b2 . |
(88.11) |
Тепер помножимо друге з рівнянь (88.9) на i й віднімемо його від четвертого. Отримаємо:
(n − i)eβl a |
2 |
− (n + i)e−βlb = 0 . |
(88.12) |
|
2 |
|
Вирішивши спільно рівняння (88.11) і (88.12), знайдемо, що
a2 = |
2i(n + i)e−βl |
, |
|
(n + i)2 e−βl − (n − i)2 eβl |
|||
|
|
||
b2 = |
2i(n − i)eβl |
. |
|
(n + i)2 e−βl − (n − i)2 eβl |
|||
|
|
Нарешті, підставивши знайдені нами значення a2 й b2 у друге з рівнянь (88.9), отримаємо вираз для a3 :
a = |
4ni |
e−iαl . |
|
||
3 |
(n + i)2 e−βl − (n − i)2 eβl |
|
|
|
Величина
178
bl = 
2m(U0 - E) l , h
як правило, є набагато більшою за одиницю. Тому в знаменнику виразу для a3 доданком, який містить множник e−βl , можна знехтувати у порівнянні з доданком, який містить
множник eβl (комплексні числа n + i й n − i мають однаковий модуль). Отже, можна припустити
a » - 4nie−iαl e−βl .
3 (n -i)2
Згідно з (88.10) квадрат модуля цієї величини дає ймовірність проходження частинки через потенціальний бар'єр. Урахувавши, що | n -i |= 
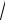n2 +1 , отримаємо
D = |
|
a |
|
2 |
» |
16n2 |
|
e−2βl , |
|
|
|
||||||
|
|
|
|
|
||||
|
|
3 |
|
|
|
(n2 +1) |
2 |
|
|
|
|
|
|
|
|
де
n2 = U0 - E = U0 -1 E E
(див. формулу (88.8)).
Вираз 16n2 /(n2 +1)2 має величину порядку одиниці. Тому можна вважати, що
|
|
|
|
|
é |
2×l |
|
|
ù |
. |
|
|
(88.13) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
D » e−2βl = expê- |
h |
2m(U0 - E)ú |
|
|
|||||
|
|
|
|
|
ë |
|
û |
|
|
|
|
||
З отриманого нами виразу випливає, що ймовірність |
|
U(x) |
|
|
|
||||||||
проходження частинки через потенціальний бар'єр істотно |
|
|
|
|
|||||||||
залежить від ширини бар'єра l |
й від величини U0 - E . |
|
E |
|
|
|
|||||||
Якщо при якійсь ширині бар'єра коефіцієнт проходження |
|
|
|
|
|||||||||
D дорівнює, припустимо, 0,01, то при збільшенні ширини |
|
|
|
|
|
|
|||||||
у |
два |
рази |
D |
буде |
дорівнювати |
|
|
|
|
|
|
||
0,012 = 0,0001, тобто зменшується в 100 разів. Той самий |
|
|
|
a |
b |
x |
|||||||
ефект у цьому випадку викликало б зростання в чотири |
0 |
||||||||||||
рази |
величини |
U0 - E . |
Коефіцієнт проходження різко |
Рисунок 88.2 |
|
|
|||||||
зменшується при збільшенні маси частинки m .
3 Подібний розрахунок можна виконати у випадку потенціального бар'єра довільної форми (рис. 88.2). У цьому разі формула (88.13) повинна бути замінена більше загальною:
é |
2 b |
|
ù |
|
|
|
|
|
|
||||
D » expê- |
|
ò |
2m(U - E)dxú |
, |
(88.14) |
|
|
||||||
ë |
h a |
û |
|
|
||
де U = U (x) .
При подоланні потенціального бар'єра частинка ніби проходить через «тунель» у цьому бар'єрі (див. заштриховану область на рис. 88.2). У зв'язку з цим розглянуте нами явище називають тунельним ефектом.
§ 89 Оператори фізичних величин. Власні функції та власні значення. Принцип суперпозиції [6]
Операторний метод широко використовується у більшості досліджень з квантової механіки. Розглянемо сутність цього методу.
179
1 Оператори. У квантовій механіці кожній фізичній величині ставиться у відповідність оператор. Під оператором мається на увазі правило, за допомогою якого одній функції (позначимо її через ϕ ) зіставляється інша функція (позначимо її через f ).
Символічно це записується так:
ˆ |
(89.1) |
f = Qϕ . |
ˆ
Тут Q – позначення оператора. Для того щоб відрізнити оператори від чисел, їх позначають
ˆ
через Q , тобто ставлять кришечку над Q або використовують інше позначення.
Таким чином, під символом оператора розуміють сукупність дій, за допомогою яких вихідна функція ( ϕ ) перетворюється в іншу функцію ( f ).
Наприклад, символ оператора Лапласа |
|
|
|
ˆ |
позначає дворазове частинне |
|||||||||||
|
|
= Q1 |
||||||||||||||
диференціювання за усіма трьома координатами x , |
|
y і z |
з подальшим підсумовуванням |
|||||||||||||
отриманих виразів. Тобто оператор Лапласа можна подати у вигляді |
|
|||||||||||||||
|
ˆ |
|
∂2 |
|
|
∂2 |
|
|
∂2 |
|
|
|
||||
= Q1 = |
|
∂x2 |
+ |
∂y2 |
+ |
∂z2 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
За допомогою оператора можемо подати множення вихідної функції |
ϕ на деяку |
|||||||||||||||
функцію U . Тоді наступне перетворення |
|
f =U ×j |
можна записати у вигляді |
ˆ |
||||||||||||
|
f = Q2ϕ , де |
|||||||||||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Q2 = U . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Використовуючи операторний підхід, рівняння Шредінгера |
|
|||||||||||||||
− |
h2 |
|
|
ψ +Uψ = Eψ |
|
|
(89.2) |
|||||||||
2m |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
можна записати в операторному вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
. |
|
|
|
|
|
(89.3) |
||
|
|
Hψ = Eψ |
|
|
|
|
|
|||||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
У цьому рівнянні символом H позначений оператор, який дорівнює |
|
|||||||||||||||
|
ˆ |
|
|
h2 |
|
|
|
|
|
|
|
|
||||
|
H = − |
2m |
|
+U . |
|
|
|
(89.4) |
||||||||
Цей оператор називають гамільтоніаном, або оператором Гамільтона. Гамільтоніан є оператором енергії E .
2 Сутність операторного методу. У квантовій механіці кожній фізичній величині ставиться у відповідність оператор. Розглядаються оператори координат, імпульсу, моменту
імпульсу і т.д. Для кожної фізичної величини q складається рівняння, |
аналогічне до |
||
рівняння Шредінгера в операторному вигляді (89.3). Воно має вигляд |
|
||
|
|
|
|
|
ˆ |
, |
(89.5) |
|
Qψ = qψ |
||
ˆ
де Q – оператор, який ставиться у відповідність фізичній величині q .
Значення q , при яких розв’язок рівняння (89.4) задовольняє стандартні умови для хвильової функції, називаються власними значеннями величини q , а самі розв’язки – її власними функціями. Власні значення величини q і беруться за можливі значення цієї
величини, які спостерігаються в експерименті.
Розглядаючи з цих позицій рівняння Шредінгера (89.3), можемо стверджувати, що воно є рівнянням для власних значень енергії ( q = E ). Оператор енергії визначається
ˆ = ˆ співвідношенням (89.4) (Q H ).
180