
Choliy.NumericaMethods.2011Dec01
.pdf
2. Нелiнiйнi рiвняння
У цьому роздiлi розглядається задача знаходження коренiв рiвняння
f(x) = 0, x [a, b],
з точнiстю ε, що задається умовою задачi. Функцiя f(x) на цьому iнтервалi має бути визначена i може належати до дуже широкого класу функцiй. Будемо також вважати, що на вказаному iнтервалi корiнь є i вiн єдиний, тобто f(a) · f(b) < 0.
Метод половинного дiлення. Знаходимо значення функцiї у середнiй то-
чцi iнтервалу:
c = a +2 b,
i перевiряємо, в якiй з половинок залишився корiнь. Це легко зробити, знайшовши
k = f(c) · f(a).
Очевидно, що якщо k < 0, то корiнь лежить у iнтервалi [a, c], якщо ж k > 0, то корiнь в iншiй половинцi. Повторюємо процедуру для iнтервалу з коренем, до тих пiр, поки |b − a| > ε.
Метод хорд. Через кiнцевi точки iнтервалу [a, b] проводимо хорду (рис. 2.1 лiва частина), яка перетинає вiсь абсцис в точцi, що є наближеням до кореня.
Скориставшись рiвнянням прямої, що проходить через двi точки (a, f(a))
та (b, f(b)) отримуємо: |
|
|
|
|
|
|
|
|
f(b) − f(a) |
= |
y − f(a) |
, |
або |
f(b) − f(a) |
= |
y − f(b) |
. |
b − a |
|
x − a |
|
|
b − a |
|
x − b |
|
Якщо тепер знайти координати точки перетину з вiссю абсцис (y = 0), маємо:
x = a |
b − a |
f(a), |
або |
x = b |
b − a |
f(b). |
||||
|
− f(b) |
− |
f(a) |
|
|
− f(b) |
− |
f(a) |
|
|
|
|
|
|
|
|
|
|
|
||
Першу формулу використовуємо коли закрiпленою залишається точка a, а другу, коли закрiпленою є точка b. Знайдене таким способом наближене зна-
11
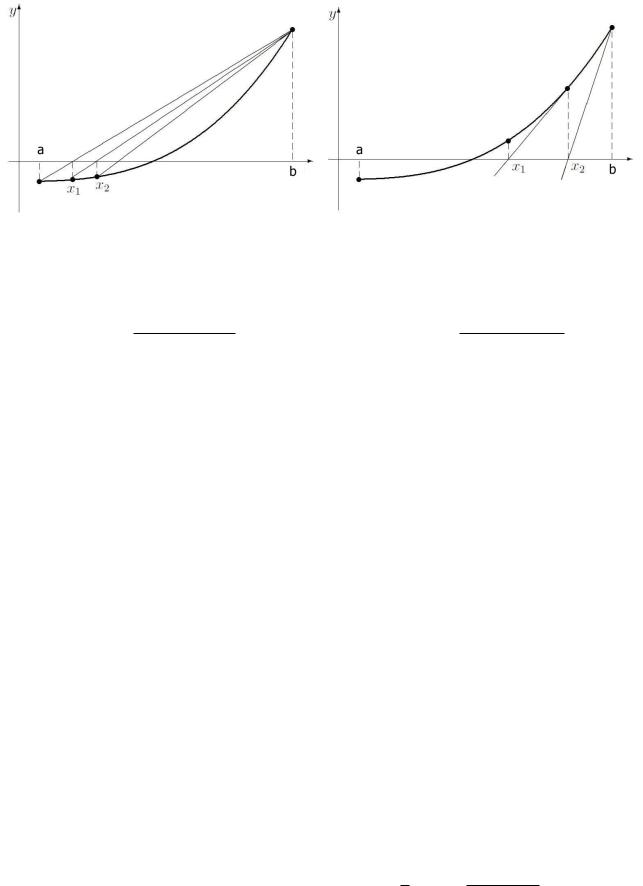
Рис. 2.1: Метод хорд та метод дотичних.
чення кореня можна використати для продовження iтерацiй, тобто |
|
|
|
||||||||||||
x |
|
= x |
b − xn |
f(x |
|
), |
або |
x |
|
= x |
xn − a |
f(x |
|
), |
|
n+1 |
n − f(b) − f(xn) |
n |
n+1 |
n − f(xn) − f(a) |
n |
||||||||||
|
|
|
|
|
|
|
|
||||||||
залежно вiд того, який кiнець iнтервалу закрiплено, доти, поки |xn+1−xn| > ε. Метод дотичних. Вибравши один з кiнцiв iнтервалу для початку процесу, проводимо через нього дотичну. Точка перетину дотичної з вiссю абсцис є наближеним значенням кореня. Нехай xn+1 = xn + h, тодi
f(xn + h) = f(xn) + f0(xn) · h.
Вважаючи вираз з лiвого боку кандидатом в коренi i поклавши його рiвним
нулю, маємо |
|
f(xn) |
|
|
|
|
f(xn) |
|
||
|
h = − |
|
|
xn+1 = xn − |
(2.1) |
|||||
|
|
, |
|
. |
||||||
|
f0(xn) |
f0(xn) |
||||||||
Теорема. Нехай |
f(a)f(b) < 0 f0 |
(x), f00 |
(x) = 0 |
x |
[a, b] |
i обидвi цi похiднi |
||||
; |
|
|
6 |
|
|
|
||||
не мiняють знаку на вказаному iнтервалi (функцiя монотонна i в неї незмiнна опуклiсть). Тодi права формула в (2.1) завжди сходиться до кореня ξ.
Будемо вважати, що умова теореми узгоджується з рис. 2.1 (права частина), тобто: f(a) < 0, f(b) > 0, f0(x) > 0 - функцiя монотонно зростає, f00(x) > 0 - функцiя опукла вниз, x0 = b. З очевиднiстю x0 > ξ. Покладемо, що xn > ξ i за iндукцiєю доведемо, що xn+1 > ξ. Для цього запишемо:
ξ= xn + (ξ − xn)
i скористаємося цим, щоб розкласти f(x) в ряд Тейлора в околицi т. xn, зберiгши лише три доданки:
f(ξ) = 0 = f(xn) + f0(xn)(ξ − xn) + 1f00(xn)(ξ − xn)2 . 2 2!
12

За умовою f00(x) > 0, тому
0 = f(xn) + f0(xn)(ξ − xn) + додатнє число,
або
f(xn) + f0(xn)(ξ − xn) < 0 ξ < xn − f0(xn) = xn+1.
Тобто, послiдовнiсть xn обмежена злiва коренем. Окрiм того,
f(xn) > 0 |
xn+1 < xn < · · · < b. |
xn+1 = xn − f0(xn) > 0 |
Таким чином, послiдовнiсть xn обмежена справа кiнцем iнтервалу. Тому:
nlim xn+1 |
= nlim xn − nlim |
f(xn) |
, |
|||
f |
(x |
) |
||||
→∞ |
→∞ |
→∞ |
0 |
n |
|
|
послiдовнiсть збiгається коли чисельник останнього доданку прямує до нуля, що доводить теорему. Iншi випадки початкових умов теореми доводяться аналогiчно. Кiнець теореми.
У нашому випадку важливим є те, що для збiжностi методу ми взяли за початкову точку той кiнець iнтервалу, у якому
f(b) · f00(b) > 0.
Це правило повинно використовуватись як загальне.
Метод простої iтерацiї. У цьому випадку рiвняння f(x) = 0 переписується до вигляду
xn+1 = ϕ(xn),
де ϕ(xn) - деяка iнша функцiя, отримана з f(x), у найпростiшому варiантi
ϕ(x) = f(x) − x.
Теорема. Нехай функцiя ϕ(x) визначена i має похiдну на [a, b], i x [a, b], ϕ(x) [a, b]. Якщо q, таке, що |ϕ0(x)| ≤ q < 1, то процес iтерацiй
сходиться x [a, b].
Запишемо вирази для двох послiдовних етапiв iтерацiї: xn = ϕ(xn−1), xn+1 = ϕ(xn).
Рiзниця цих виразiв
xn+1 − xn = ϕ(xn) − ϕ(xn−1) = (xn − xn−1) · ϕ0(c), c [xn, xn−1],
13
але |ϕ0(x)| < q, тому
|xn+1 − xn| ≤ q|xn − xn−1|,
звiдки легко отримати прямою пiдстановкою
|xn+1 − xn| ≤ qn|x1 − x0| → 0, при n → ∞.
Отже, за вказаних умов, процес iтерацiї сходиться зi швидкiстю геометричної прогресiї. Кiнець теореми.
Система двох рiвнянь. Системою двох нелiнiйних рiвнянь з двома змiнними є:
F (x, y) = 0 .
G(x, y) = 0
Якщо (ξ, η) - точний, а (xn, yn) - наближений коренi, то поклавши
|
|
|
|
|
|
|
ξ |
= xn + hn , |
|
|
|
η |
= yn + ln |
|
маємо |
|
|
|
|
|
0 |
= F (xn + hn, yn + ln) = F (xn, yn) + hnFx0(xn, yn) + lnFy0(xn, yn) |
, |
|
0 |
= G(xn + hn, yn + ln) = G(xn, yn) + hnGx0 (xn, yn) + lnGy0 (xn, yn) |
|||
або в виглядi системи лiнiйних рiвнянь:
F (xn, yn) |
|
Fx0(xn, yn) Fy0(xn, yn) |
G(xn, yn) |
= − Gx0 (xn, yn) Gy0 (xn, yn) |
Матриця цiєї системи є матрицею Якобi:
J(xn, yn) = Fx00(xn, yn) Fy00(xn, yn)
Gx(xn, yn) Gy(xn, yn)
а розв’язок:
· |
hn |
ln . |
,
η |
= |
yn+1 |
= |
yn |
− J−1(xn, yn) |
G(xn, yn) . |
ξ |
|
xn+1 |
|
xn |
|
F (xn, yn) |
Якщо рiзниця мiж (xn+1, yn+1) та (xn, yn) менша прийнятого критерiю точностi, то (xn+1, yn+1) приймається коренем i iтерацiї закiнчуються. У iншому випадку це лише чергове наближення.
Отримане спiввiдношення легко узагальнюється. Запишемо систему нелiнiйних рiвнянь у виглядi:
~ ~
K(ρ~) = 0,
14

iтерацiйною схемою для якої, очевидно, буде
− −1 ~ ρ~n+1 = ρ~n J (ρ~n)K(ρ~n).
Записане спiввiдношення є багатовимiрною версiєю методу дотичних. Зовсiм легко записати вираз для методу простої iтерацiї:
~ |
~ |
ρ~ = ϕ~(ρ~), |
K(ρ~) = 0 |
||
який буде збiгатися за умови |J| ≤ q < 1.
Знаходження коренiв полiнома. Тут i надалi полiномом (багаточленом) називається вираз (у загальному випадку його коефiцiєнти - комплекснi чи-
сла):
P (x) = a0xn + a1xn−1 + · · · + an−1x + an.
Нагадаємо два твердження, якi матимуть значення для подальшого викладу. По-перше, це головна теорема алгебри, згiдно з якою довiльний полiном степеня n має n коренiв, загалом комплексних. По-друге, полiном непарного степеня має хоча б один дiйсний корiнь.
Знайдемо межi, в яких мають лежати коренi. Для цього покладемо
A = max(|a1|, |a2|, . . . , |an|).
Для |x| > 1
|P (x)| = |a0xn+a1xn−1+· · ·+an−1x+an| ≥ |a0xn|−(|a1xn−1+· · ·+an−1x+an|) ≥
a x |
n |
− |
A( x |
n−1 + x |
n−2 + |
· · · |
+ x |
+ 1) = |
|
|
a |
x |
n |
− |
A |
|x|n − 1 |
> |
|||||
|
|
|
|x| − 1 |
|||||||||||||||||||
≥ | |
0|| | |
|
| | |
| | |
|
|
| | |
|
|
|
| |
0|| | |
|
|
|
|
||||||
|
|
|
|
> |a0||x|n − A |
|x|n |
|
= |x|n |a0| − |
|
A |
. |
|
|
|
|||||||||
|
|
|
|
x |
1 |
x 1 |
|
|
|
|||||||||||||
Тобто, |
|
|
|
|
|
|
| | − |
|
|
|
|
|
|
| |
| − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|P (x)| > |x|n |a0| − |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|x| − 1 |
|
|
|
|
|
|
|||||||||||
Для тiєї частини числової площини, де
|a0| − |
A |
> 0, |
|x| > |
A |
+ 1, |
||
|
|
|
|
||||
|x| − 1 |
|a0| |
||||||
модуль полiнома |P (x)| > 0, що означає вiдсутнiсть коренiв. Тому вираз
A
|x| < |a0| + 1,
15

можна вважати верхньою границею модулiв коренiв полiнома. Щоб знайти нижню границю модуля коренiв покладемо x = 1/y:
|
a0 |
|
a1 |
|
an−1 |
1 |
|
n |
1 |
|
||
P (x) = |
yn |
+ |
yn−1 |
+ · · · + |
y |
+ an = |
yn |
(a0 |
+ a1y + · · · + any |
) = |
yn |
Q(y). |
Використавши попередню процедуру до полiнома Q(y), знаходимо для його
коренiв |
|
|
max(|an−1|, |an−2|, . . . , |a0|) |
|
B |
|
|||||
y |
| |
< |
+ 1 = |
+ 1, |
|||||||
|an| |
|||||||||||
| |
|
|an| |
|
|
|
|
|
|
|||
але тодi |
|
|
|
1 |
|
|
|
|
|||
|
|
|
|x| > |
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
B |
+ 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|an| |
|
|
|
|
|||
що i є нижньою границею модулiв коренiв полiнома.
Метод Лобачевського. Будемо вважати, що коренi вiдсортованi по модулю вiд найбiльшого до найменшого. Скористаємось узагальненою теоремою Вiєта, згiдно з якою
|
−a |
a1 |
= x1 + x2 + · · · + xn |
|
|
|||||
a20 |
|
|
|
|||||||
|
|
|
|
|
|
= x1x2 + x2x3 + |
· · · |
+ xn−1xn |
|
|
|
a0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
||
|
|
|
|
|
|
= x1x2x3 + x2x3x4 + + xn 2xn 1xn |
. |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
a |
0 |
|
|
|
|
· · · − − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n an |
. . . |
|
|
|
|
||
|
( 1) |
|
|
= x1x2 . . . xn |
|
|
|
|
||
|
|
|
|
a0 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||
Оскiльки коренi сортованi, то x1 > x2 > · · · > xn i тодi:
−a1 aa20
a0
−a3
a0
a
(−1)n n
a0
=x1(1 + E1)
=x1x2(1 + E2)
= x1x2x3(1 + E3) .
. . .
=x1x2 . . . xn
У методi Лобачевського вважається, що Ei < 1, i, тому, знехтувавши усiми Ei, знаходимо наближення до коренiв, якi потiм уточнюємо одним iз розглянутих ранише методiв. Зрозумiло, що точнiсть початкового наближення дуже
16

залежить вiд того, наскiльки сильно коренi вiдрiзняються один вiд одного. Для покращання початкових можна взяти
P (x)P (−x) = a0(x − x1)(x − x2) . . . (x − xn) · a0(x + x1)(x + x2) . . . (x + xn) =
= a20(x2 − x21)(x2 − x22) . . . (x2 − x2n).
Коренями цього полiнома є квадрати коренiв попереднього, тому можна сподiватися, що вiдношення мiж коренями зростуть i це буде на користь точностi. Метод Лагера. Вiзьмемо першу та другу похiднi вiд прологарифмованого
полiнома: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
P (x) |
= a0(x − x1)(x − x2) . . . (x − xn) |
|
|
|
|
|||||||||
|
|
|
|
ln P (x) |
= ln a0 + ln (x − x1) + ln (x − x2) + · · · + ln (x − xn) |
|
||||||||||||
|
|
d ln P (x) |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
. |
|||
|
2 |
|
dx |
= |x − x1| + |x − x2| + · · · + |x − xn| = G |
||||||||||||||
|
|
|
||||||||||||||||
− |
d |
ln P (x) |
1 |
|
1 |
|
+ · · · + |
1 |
|
|
||||||||
|
|
|
|
|
= |
|
+ |
|
|
= H. |
|
|||||||
|
|
|
dx2 |
(x − x1)2 |
(x − x2)2 |
(x − xn)2 |
|
|||||||||||
Будемо також вважати, що корiнь x1 знаходиться на вiдстанi a вiд деякого значення x, а iншi коренi - на вiдстанi b вiд нього. Тодi
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
G = |
1 |
|
+ |
n − 1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
H |
= |
1 |
|
|
+ |
n − 1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
звiдки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
G ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(n − 1)(nH − G2) |
|
|
||||||||||||||||
Величини |
G |
та |
H |
|
|
|
|
|
|
|
|
таких мiркувань: |
|
|
|||||||||||||||
|
|
знаходяться зp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
d |
lndx( |
) |
= |
|
P0(x) |
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
P x |
|
|
|
|
P (x) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
d2 ln P (x) |
|
|
P 00(x)P (x) |
|
|
P 0 |
(x)P 0 |
(x) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
2 |
(x) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскiльки вираз для P (x) вiдомий, то P 0(x) та P 00(x) отримати неважко.
17
Задачi. У цьому роздiлi задачi мiстять по чотири приклади i однiй системi рiвнянь. Кожен приклад має розв’язуватись iншим методом: методом половинного подiлу, методом хорд, методом дотичних, методом простої iтерацiї. Iнтервал, на якому є корiнь потрiбно знаходити самостiйно. Якщо iнтервал вказано, то потрiбно знайти корiнь, що попадає в цей iнтервал. Систему слiд розв’язувати будь-яким методом на власний розсуд. Точнiсть розв’язання повинна задаватись наперед.
|
|
|
|
sin (x + 1) − y = √ |
|
|
|
|
|
|
|
|
|
tg (xy + 0.3) = x2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
2 |
; |
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2x + cos y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5x2 + y2 = 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1. |
|
3x4 + 4x−3 |
|
|
12x2 |
|
|
|
5 = 0, |
6. |
|
|
|
2x4 |
|
|
x2 |
|
10 = 0, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
− |
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
x |
|
|
− |
x − |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||
|
|
0.5 + 1 = (x |
− |
2) , |
|
|
|
|
|
|
|
|
|
|
|
log3 ( |
|
|
+ 1) = 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
[ |
|
2π . . . 2π]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
. |
|
|
|
|
|
|
|
|||||
|
|
− |
3) cos x = 1, |
|
|
|
|
− |
|
cos (x + 0.5) = x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x2 + y2 = 1−, |
|
x, y > 0 |
|
|
|
− |
2) + x = 0 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
5x + 3x = 0, |
|
|
1.6x = 0 |
; |
2 arctg x |
1/(2x3) = 0, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
x4 |
|
sin (x + y) |
|
|
x4 |
sin (x + 0.5) |
− y = 1 ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x 1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
18x3−+ 6 = 0, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − − |
|
|
|
x |
= 0, |
|
|
|
|
|
|
|
|
|
x22−x = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
− |
|
2 + 0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
(x |
|
|
3) |
2 |
|
|
log (x + 11) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
[ |
|
|
|
π/2 . . . π/2]. |
|||||||||||||||||||||||
|
|
|
− |
|
|
· |
tg x = x + 1, |
|
|
|
|
− |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 = 1− |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
cos (y |
− |
1) + x = √ |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
sin (x + y) |
|
|
1.3x = 0 |
|||||||||||||||||||||||||||
|
|
|
|
|
sin x + 2y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
x4 + 4x3 |
|
|
|
8x2 |
|
|
17 = 0, |
|
|
|
|
x3 |
|
|
2x2 + 3x 3 = 0, |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||
3. |
|
exp (−2x) − 2x + 1 = 0, |
8. |
|
|
|
5 |
|
− |
6x |
|
− |
3 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
− − |
|
2 |
, |
|
|
|
|
|
|
|
|
|
2x2− 0.5x |
|
|
|
3 = 0, |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0.5 + 1 = (x + 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
cos (2x) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x lg (x + 1) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
x2 |
+ 2y2 |
|
|
− |
|
|
|
|
2 |
; |
|
|
|
|
|
|
|
|
0.8x2 |
|
+ 2y2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 ; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
tg (xy + 0.1) = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
tg (xy) = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4. |
3x + 2x |
|
|
|
2 = 0, |
|
|
1 = 0, |
9. |
|
|
|
2 arctg x |
|
3x + 2 = 0, |
||||||||||||||||||||||||||||||||||||||||||||
|
2x4 |
|
|
|
|
8x−3 + 8x2 |
|
|
|
|
|
2x4 + 8x3−+ 8x2 |
|
|
|
|
|
1 = 0, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
((x |
|
− |
|
2 |
|
|
|
1)2 |
x |
− |
|
|
|
|
|
|
|
|
|
|
|
|
(log |
(x + 2))(x −1) = 1, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2) |
|
|
|
|
= 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− √ |
|
|
|
|||||||||||
|
|
(x |
− |
2) cos x = 1, |
|
|
|
x |
|
[ |
− |
2π . . . 2π]. |
|
sin (x |
− |
|
0.5) |
− |
x + |
|
|
|
2/2 = 0. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2x − sin (y − 0.5) = 1 |
|
|
|
x − sin (y + 1) = 0.8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
cos x + y = 1.5 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
sin (x − |
1) = 1.3 |
− y ; |
||||||||||||||||||||||||||||||||||||||
5. 2x3 |
|
−9x2− |
|
60x + 1 = 0, |
|
|
3x4 |
+ 4x3 |
|
|
|
12x 5 = 0, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
3x−1 |
|
|
|
4 |
|
|
|
x = 0, |
|
|
|
|
|
|
|
|
|
10. |
|
2 exp (x) + 3x |
− |
1 = 0, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
||||||||||||
|
|
(x |
|
|
2 |
|
|
|
|
|
|
|
|
|
2) = |
|
1, |
|
x log |
(x + 1) = 2, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3) |
|
log0.5 (x |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
1. |
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
5 sin x = x |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (x + |
|
2/4) = x |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
18
|
x +−sin (y + 1) = 0.8 |
; |
||||||||||||
|
x4 |
2y |
|
cos (x + 1) = 0 |
|
|||||||||
11. |
|
18x2 + 6 = 0,− |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg (x + 1) + 3x |
|
|
2 = 0, |
|||||||||
|
(x |
− |
2 |
x |
= 1, |
|
|
|
|
|
||||
|
|
− |
2) 2 |
|
|
|
|
|
||||||
|
|
|
2 |
20 sin x = 0. |
|
|
|
|
||||||
|
x |
|
− |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
cos (x + 0.5) − y = 2 |
; |
|||||||||||
|
|
|
||||||||||||
|
|
|
sin y − 2x = 1 |
|
|
|
|
|||||||
12. |
|
|
|
− x3 |
|
− |
3x2 |
+ 2x |
|
5 = 0, |
||||
x4 |
|
|
||||||||||||
|
|
2x |
|
3x |
|
|
2 = 0, |
|
|
|
|
|||
|
|
|
−x |
|
− |
|
|
|
2 |
− |
|
|||
|
|
0.5 + 1 = (x |
− |
2) , |
|
|
||||||||
|
|
(x |
|
|
|
|
|
|
|
|
|
|
||
|
|
− |
3) cos x = 1. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (x + 0.5) − y = 2 ;
sin y − 2x = 1
13. |
|
2x3 |
|
|
9x2 |
|
|
60x + 1 = 0, |
||||||
|
|
3x |
+ 2 + x = 0, |
|
|
|
||||||||
|
(x |
|
− |
2 |
|
− |
|
|
|
3) = |
1, |
|||
|
|
− |
4) |
log0.5 (x |
− |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|||
|
|
5 sin x = x |
− |
0.5. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sin (x + 2) − y = 1.5
x + cos (y − 2) = 0.5 ;
|
|
2x4 |
−x2 |
|
|
10 = 0, |
|
|
||||||
14. |
|
exp ( 2x) |
− 2x + 1 = 0, |
|||||||||||
|
|
|
x− |
|
− |
|
(x + 1) |
2 |
, |
|||||
|
|
0.5 |
|
3 = |
− |
|
||||||||
|
|
|
2 |
− |
|
|
|
|
1. |
|
|
|
||
|
x |
|
cos 2x = |
− |
|
|
|
|||||||
|
|
x2 |
+ y2 |
|
|
|
|
|
||||||
|
|
= 1− |
|
|
; |
|||||||||
|
x4 |
sin (x + y) |
|
1.5x = 0.1 |
||||||||||
15. |
|
18x−2 + 6 = 0, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg (x |
|
1) + 2x = 0, |
||||||||||
|
(x |
− |
|
2 |
x |
= 1, |
|
|
|
|||||
|
|
− |
2) 2 |
|
|
|
||||||||
|
|
|
2 |
10 sin x = 0. |
|
|
||||||||
|
x |
|
− |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin (y + 1) − x = 1.2 ;
2y + cos x = 2
3x + 5x − 2 = 0,
16. 3x4 + 4x3 − 12x2 + 1 = 0,
0.5x + 1 = (x − 2)2, (x + 3) cos x = 1.
|
|
y2 + y2 = 1− |
|
|
; |
||||||
|
3x |
|
2x |
|
5 = 0, |
|
|
||||
|
|
|
sin (x + y) |
|
1.2x = 0.1 |
||||||
17. |
3x4−+ 8x−3 + 6x2 |
|
10 = 0, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
2 |
|
0.5 |
x |
|
|
− |
|
|
|
|
|
− |
|
− |
3 = 0, |
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
x lg (x + 1) = 1. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg (xy + 0.2) = x2 |
; |
||||||||
|
0.6x2 + y2 = 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
arctg (x − 1) + 2x − 3 = 0,
18.4
x − x − 1 = 0,
(x − 1)22x+1 = 1,
tg3 x = x + 1, x [−π/2 . . . π/2].
|
|
y2 + x2 |
= 1 |
|
|
− |
; |
|
|
sin (y + x) = 1.5x |
|
0.1 |
|||
|
3x4 + 4x3− 12x2 |
|
5 = 0, |
||||
|
|
|
|
|
|
|
|
19. |
|
2 exp (x) |
2x − 3 = 0, |
|
|||
|
|
− |
− |
|
|
|
|
|
x log3 (x + 1) = 1, |
|
|
|
|||
|
|
|
3 |
. |
|
|
|
|
cos (x + 0.5) = x |
|
|
|
|||
|
|
|
|
|
|
|
|
cos (y − 1) + x = 0.5 ;
y − cos x = 3
|
|
3x4 + 4x3 |
|
|
12x2 |
|
|
5 = 0, |
||||||
20. |
|
arctg x + 2x − |
1 = 0, |
|
|
|||||||||
|
|
|
|
|
− |
|
|
− |
|
|
|
|||
|
|
(x + 2) log2 x = 1, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin (x + 1) = 0.5x. |
|
|
|
|
|||||||||
|
|
cos (x − 1) + y = √2 ; |
||||||||||||
|
|
|||||||||||||
|
|
sin y + 2x = 2 |
|
|
|
|
|
|||||||
21. |
x4 + 4x3 |
− |
8x2 |
|
17 = 0, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 arctg x |
|
|
x + 3 = 0, |
|
|
|||||||
|
|
|
|
− |
|
|
− |
|
2 |
|
0.5, |
|||
|
|
2 sin (x + π/3) = x |
|
− |
||||||||||
|
|
4 tg x |
|
x + 2 = 0. |
|
|
|
|||||||
|
|
− |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos y + x = 1.5
2y − sin (x − 0.5) = 1 ;
3x − 2x + 5 = 0,
22. 3x4 + 8x3 + 6x2 − 10 = 0,
2x2 − 0.5x − 2 = 0, x lg (x + 1) = 1.
19
|
|
|
tg (xy + 0.1) = x2 |
; |
||||||
|
0.9x2 + 2y2 = 1 |
|||||||||
23. |
|
3x4 |
|
8x−3 |
18x2 + 2 = 0, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
|
−x |
= 0, |
|
||
|
x |
|
− |
4 + 0.5 |
|
|
||||
|
|
(x |
|
2 |
lg (x + 12) = 1. |
|||||
|
|
− |
2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
sin (y − 1) + x = 1.3
y − sin (x + 1) = 0.8 ;
exp (x) + x + 1 = 0,
24. 4 2
2x − x − 10 = 0,
0.5x − 3 = (x + 2)2, x2 cos (2x) = −1.
25. |
|
x2 + y2 = 1 |
− |
; |
|||||||||
3x3 arctg x − 1 = 0, |
|
0.1 |
|||||||||||
|
x4 |
sin (x + y) = 1.1x |
|
||||||||||
|
|
|
x |
|
1 = 0, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
− |
|
|
−2 |
x |
= 1, |
|
|
|
||
|
|
|
|
1) 2 |
|
|
|
|
|||||
|
|
3− |
|
|
|
|
|
|
|
|
1. |
||
|
tg (x)/3 + tg (x) = x |
− |
|||||||||||
|
|
x2 |
− y−2 = 3/4 |
|
|
||||||||
|
|
−1 |
|
||||||||||
|
|
|
sin (x |
|
y) − xy = |
; |
|||||||
26. |
3x4 |
|
|
8x3− |
|
18x + 2 = 0, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 arctg x |
|
x + 3 = 0, |
|
|
|||||||
|
|
|
− |
|
|
− |
|
|
|
|
|||
2 sin (x + π/3) = 0.5x2 − 1, 4 lg x − x + 2 = 0.
x2 + y2 = 2
x2 − y2 = 1 ;
27. |
|
2x3 |
|
|
9x2 |
|
−60x + 1 = 0, |
||||||
|
|
3x3 arctg x |
|
1 = 0, |
|
|
|
||||||
|
|
− |
|
x) |
− |
|
|
|
1, |
|
|||
|
log2 |
( |
− |
· |
(x + 2) = |
− |
|
||||||
|
|
|
|
|
|
|
|
|
1. |
||||
|
sin (x + π/3) |
− |
0.5x = |
− |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
sin (y + 2) − x = 1.5 ;
y + cos (x − 2) = 0.5
3x + 2x − 5 = 0,
28. x4 − 4x3 − 8x2 + 1 = 0,
x2 − 3 + 0.5x = 0,
(x − 2)2 lg (x + 13) = 1.
|
|
|
|
tg (xy + 0.2) = x2 |
|
||
29. |
x2 + 2y2 = 1 |
; |
|||||
|
3x4 + 4x−3 12x2 + 1 = 0, |
||||||
|
|
|
|
|
|
|
|
|
|
arctg (x |
1) + 2x = 0, |
||||
|
(x |
|
2 |
x− |
|
||
|
|
− |
2) 2 |
= 1, |
|
||
|
|
|
2 |
20 sin x = 0. |
|
||
|
x |
|
− |
|
|||
|
|
|
|
|
|
|
|
sin (x + 0.5) − y = 1.2 ;
cos (y − 2) + x = 2
30. |
|
3x−1 − 2 − x = 0, |
|
10 = 0, |
|
||||||||||
|
3x4 + 8x3 + 6x2 |
− |
|
||||||||||||
|
|
(x |
|
4) |
2 |
|
log0.5 |
|
|
3) = |
|
1, |
|||
|
|
− |
|
· |
(x |
− |
− |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
5 sin x = 1/x. |
|
|
|
|
|
|
|
||||||
|
|
|
sin (x + y) |
1.2x = 0 |
|
|
|||||||||
|
x2 + y2 = 2− |
|
|
|
|
|
; |
|
|||||||
|
x4 |
|
x3 + x2 x + 1 = 0, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31. |
|
arctg (x − 0.5) − 2.5x − 3.5 = 0, |
|||||||||||||
|
(x |
− |
|
|
3 |
|
x+0−.5 |
|
= 1, |
|
|
|
|||
|
|
|
0.5) 2 |
|
|
|
|
|
|||||||
|
|
3− |
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
tg x + 3 tg x = x |
− |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sin (x + y) − 1.1x = 0.1
|
x4 |
x2 − y2 |
= 1 |
|
; |
||
32. |
|
|
|||||
+ x3 |
|
x2 + x 1 = 0, |
|
||||
|
|
|
|
|
|
|
|
|
|
arctg (x + 0.5) + 2.5x + 3.5 = 0, |
|||||
|
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
(x + 0.5)32x−0.5 = 1, tg3 x − 3 tg x = x + 1.
20
