
ChM_teory2
.PDF
|
|
|
ȼ ɦɟɬɨɞɿ ɇɶɸɬɨɧɚ, ɞɥɹ ɹɤɨɝɨ |
|
f (xk ) |
ɡɚɦɿɧɸɽɬɶɫɹ ɧɚ |
|
f (xk ) |
f (xk 1 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
xk |
xk |
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɞɚɽ ɦɟɬɨɞ ɫɿɱɧɢɯ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
xk |
|
|
|
|
|
|
|
xk |
|
|
|
|
|
xk |
1 |
|
|
|
|
|
|
|
f (xk |
) k = 1,2…; x0,x1- ɡɚɞɚɧɿ |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk 1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Ɂɚɞɚɱɚ 5 Ⱦɚɬɢ ɝɟɨɦɟɬɪɢɱɧɭ ɿɧɬɟɪɩɪɟɬɚɰɿɸ ɦɟɬɨɞɭ ɫɿɱɧɢɯ . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.5. Ɂɛɿɠɧɿɫɬɶ ɦɟɬɨɞɭ ɇɶɸɬɨɧɚ [ɋȽ, 199-203] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ɍɟɨɪɟɦɚ 1 ɇɟɯɚɣ f (x) C2 >a,b@; |
|
|
|
|
|
|
|
|
ɩɪɨɫɬɢɣ ɞɿɣɫɧɢɣ ɤɨɪɿɧɶ ɪɿɜɧɹɧɧɹ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɿ f c(x) |
0 ɩɪɢ x Ur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r . əɤɳɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
x : |
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
M2 |
|
x0 |
x |
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
f c(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ɞɟ m1 |
|
|
min |
|
|
|
|
|
,M2 |
|
|
|
|
|
|
(x) |
|
|
, ɬɨ ɞɥɹ x0 |
|
|
Ur ɦɟɬɨɞ ɇɶɸɬɨɧɚ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
max |
f |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Ur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
xk |
|
|
|
|
|
|
|
|
f c(xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||||||||||||||||||||
ɡɛɿɝɚɽɬɶɫɹ ɿ ɦɚɽ ɦɿɫɰɟ ɨɰɿɧɤɚ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d q2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
x |
|
|
|
|
x |
. |
|
|
|
|
(4) |
|||||||||||||||||||||||||||||
Ɂ (3) ɦɚɽɦɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk ) |
|
|
|
|
|
|
|
|
|
|
|
(xk |
|
|
x) f (xk ) |
f (xk ) |
|
F(xk ) |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
|
|
|
|
|
|
x |
|
xk |
|
|
f c(xk ) |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f c(xk ) |
|
|
|
|
|
|
|
f c(xk ) |
, |
(5) |
||||||||||||||||||||||||||||
ɞɟ F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) , ɬɚɤɚ, ɳɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
(x |
|
|
x) f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) F(x) 0; 2) F (x) (x x) f (x). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ɍɨɞɿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) x³k Fc(t)dt |
|
|
x³k (t |
|
) f cc(t)dt . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F( |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(xk ) |
|
x |
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ɍɚɤ ɹɤ |
|
|
|
|
|
ɧɟ |
ɦɿɧɹɽ |
|
ɡɧɚɤ ɧɚ |
ɜɿɞɪɿɡɤɭ |
ɿɧɬɟɝɪɭɜɚɧɧɹ, ɬɨ |
ɫɤɨɪɢɫɬɚɽɦɨɫɹ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(t |
x) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɬɟɨɪɟɦɨɸ ɩɪɨ ɫɟɪɟɞɧɽ ɡɧɚɱɟɧɧɹ: |
|
|
|
|
|
|
|
|
(t |
|
x)dt |
|
|
|
|
|
2 |
|
|
|
|
f cc([k ) , |
|
|
|
(6) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(xk ) |
|
|
f cc([k ) ³ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
ɞɟ [k |
|
|
Tk (xk |
|
|
|
|
|
|
|
|
|
|
Tk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xk |
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1. Ɂ (5),(6) ɦɚɽɦɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
x),0 |
|
|
|
|
|
f cc([k ) |
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
x |
|
|
|
|
|
|
|
|
2 f c(xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xk |
|
|
x |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ⱦɨɜɟɞɟɦɨ ɨɰɿɧɤɭ (3) ɡɚ ɿɧɞɭɤɰɿɽɸ. Ɍɚɤ ɹɤ x0 |
|
Ur , ɬɨ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[0 |
|
|
|
|
|
|
|
T0 (x0 |
|
|
|
|
T0 |
|
|
|
x0 |
|
|
|
|
[0 Ur . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
f cc( 0 ) |
|
|
d M |
|
|
|
x |
|
|
|
x) |
|
|
|
|
|
x |
r |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ɍɨɞɿ |
|
|
|
|
|
2 , ɬɨɦɭ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
d |
|
|
|
|
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
2 |
|
x0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r , x1 Ur , |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
(x |
0 |
|
|
|
x |
M |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
x |
|
|
|
q |
x0 x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ɇɢ ɞɨɜɟɥɢ ɬɜɟɪɞɠɟɧɧɹ (4) ɩɪɢ n |
|
|
|
1. ɇɟɯɚɣ ɜɨɧɨ ɫɩɪɚɜɞɠɭɽɬɶɫɹ ɩɪɢ n |
k |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d q2k 1 |
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
[k |
|
|
|
|
|
|
|
|
|
|
|
|
Tk (xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Ur |
xk x |
|
|
|
|
x |
|
|
|
|
r, |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x) |
|
r . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ɍɨɞɿ xk , k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ⱦɨɜɟɞɟɦɨ (4) ɞɥɹ n |
|
|
k 1. Ɂ (7) ɦɚɽɦɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
k |
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
2 |
x |
0 |
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
|
x |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d q2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2k 1 2 |
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2k 1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
M |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
x |
|
|
|
q |
x |
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ɍɚɤɢɦ ɱɢɧɨɦ (4) ɫɩɪɚɜɞɠɭɽɬɶɫɹ ɞɥɹ n |
|
|
|
|
|
|
k |
|
1. Ɂɧɚɱɢɬɶ (4) ɜɢɤɨɧɭɽɬɶɫɹ ɿ ɞɥɹ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɞɨɜɿɥɶɧɨɝɨ n . Ɍɚɤɢɦ ɱɢɧɨɦ xn |
|
nofo x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Ɂ (4) ɦɚɽɦɨ ɨɰɿɧɤɭ ɤɿɥɶɤɨɫɬɿ ɿɬɟɪɚɰɿɣ ɞɥɹ ɞɨɫɹɝɧɟɧɧɹ ɬɨɱɧɨɫɬɿ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ª |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
º |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
« |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n t «log2 (1 |
ln |
b |
a |
)» 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln q |
|
|
|
|
|
|
|
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
« |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ʉɚɠɭɬɶ, ɳɨ ɿɬɟɪɚɰɿɣɧɢɣ ɦɟɬɨɞ ɦɚɽ ɫɬɟɩɿɧɶ ɡɛɿɠɧɨɫɬɿ m, ɹɤɳɨ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
O |
xk |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
f cc([k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Ⱦɥɹ ɦɟɬɨɞɭ ɇɶɸɬɨɧɚ |
|
|
|
|
|
|
|
|
xk 1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
c(xk ) |
|
|
|
|
|
|
|
|
xk 1 x |
|
xk |
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
f |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Ɂɧɚɱɢɬɶ ɫɬɟɩɿɧɶ ɡɛɿɠɧɨɫɬɿ ɦɟɬɨɞɭ ɇɶɸɬɨɧɚ m=2. Ⱦɥɹ ɦɟɬɨɞɭ ɩɪɨɫɬɨʀ ɿɬɟɪɚɰɿʀ ɿ
ɞɿɥɟɧɧɹ ɧɚɜɩɿɥ m=1. |
@ |
x C2 a,b@ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
> |
ɬɚ |
|
ɩɪɨɫɬɢɣ ɤɨɪɿɧɶ |
|
|||||||
Ɍɟɨɪɟɦɚ |
|
2 |
ɇɟɯɚɣ |
f |
x |
ɪɿɜɧɹɧɧɹ |
f (x) 0 |
|||||||||||
|
f c( |
x |
) |
|
0 |
|
x |
a,b . əɤɳɨ |
f (x) f (x) |
0 |
f (x) f |
(x) |
0 ɬɨ ɞɥɹ ɦɟɬɨɞɭ |
|||||
ɇɶɸɬɨɧɚ |
ɩɪɢ |
x0 |
b ɩɨɫɥɿɞɨɜɧɿɫɬɶ |
ɧɚɛɥɢɠɟɧɶ |
xk ` |
ɦɨɧɨɬɨɧɧɨ |
ɫɩɚɞɚɽ |
|||||||||||
(ɦɨɧɨɬɨɧɧɨ ɡɪɨɫɬɚɽ ɩɪɢ x0 |
a ). |
|
|
|
|
f (x) f cc(x) 0. |
|
|||||||||||
Ɂɚɞɚɱɚ 6 Ⱦɨɜɟɫɬɢ ɬɟɨɪɟɦɭ 2 ɩɪɢ ɚ) |
f (x) f |
(x) |
0, ɛ) |
|
||||||||||||||
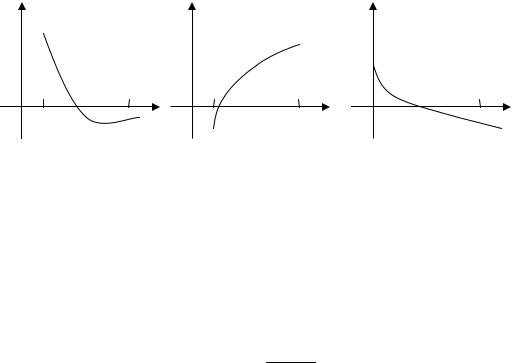
Ɂɚɞɚɱɚ 7 Ɂɧɚɣɬɢ ɫɬɟɩɿɧɶ ɡɛɿɠɧɨɫɬɿ ɦɟɬɨɞɭ ɫɿɱɧɢɯ [Ʉɚɥɢɬɤɢɧ ɇ.ɇ., ɑɢɫɥɟɧɧɵɟ ɦɟɬɨɞɵ, ɫ. 145-146]
əɤɳɨ |
f (a) f cc(a) |
|
0 ɬɚ f |
(x) ɧɟ ɦɿɧɹɽ ɡɧɚɤ, ɬɨ ɩɨɬɪɿɛɧɨ ɜɢɛɢɪɚɬɢ |
|||
x0 a ; ɩɪɢ ɰɶɨɦɭ {xk }n |
|
. |
|
|
|
||
x |
|
|
|
||||
əɤɳɨ |
f (b) f c(b) |
0 , ɬɨ x0 |
b; ɦɚɽɦɨ {xk }p |
|
. ɉɨɹɫɧɟɧɧɹ ɧɚ ɪɢɫɭɧɤɭ |
||
x |
|||||||
2. |
|
|
|
|
|
|
|
12
|
|
|
|
x0=a |
|
|
|
|
|
x0=a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0=b |
|
|
|
|
|||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɢɫ. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ɂɚɭɜɚɠɟɧɧɹ 1 əɤɳɨ |
|
ɪ-ɤɪɚɬɧɢɣ ɤɨɪɿɧɶ ɬɨɛɬɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x |
|
|
|
|
|
|
0, |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
f (m) ( |
|
) 0,m |
|
|
|
|
1; f ( p) ( |
|
) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x |
0,1,..., p |
x |
|
|
|
|
|||||||||||||||||||||||||
ɬɨ ɜ ɦɟɬɨɞɿ ɇɶɸɬɨɧɚ ɧɟɨɛɯɿɞɧɚ ɧɚɫɬɭɩɧɚ ɦɨɞɢɮɿɤɚɰɿɹ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
xk 1 |
xk |
p |
f (xk |
) |
ɿ q |
|
|
x0 x |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
f c(xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mp p( p 1) |
|
|
|
|
||||||||||||||||
Ɂɚɭɜɚɠɟɧɧɹ 2 |
Ɇɟɬɨɞ |
ɇɶɸɬɨɧɚ |
ɦɨɠɧɚ |
ɡɚɫɬɨɫɨɜɭɜɚɬɢ ɿ |
ɞɥɹ |
ɨɛɱɢɫɥɟɧɧɹ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (zk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɤɨɦɩɥɟɤɫɧɨɝɨ |
ɤɨɪɟɧɹ |
|
|
|
zk 1 zk |
|
|
f c(zk ) |
. ȼ |
ɬɟɨɪɟɦɿ |
ɩɪɨ |
ɡɛɿɠɧɿɫɬɶ |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x0 x |
M2 |
|
ɞɟ m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɭɬ |
|
|
|
- ɦɨɞɭɥɶ |
||||||||||||||
q |
, |
|
|
|
min |
f (z) |
, M |
2 |
max |
f |
(z) |
. |
|
|
|
|
z |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2m1 |
1 |
|
|
Ur |
|
|
|
|
|
|
Ur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ɤɨɦɩɥɟɤɫɧɨɝɨ ɱɢɫɥɚ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ɉɟɪɟɜɚɝɢ |
ɦɟɬɨɞɭ |
|
|
|
ɇɶɸɬɨɧɚ: |
|
1) ɜɢɫɨɤɚ |
ɲɜɢɞɤɿɫɬɶ ɡɛɿɠɧɨɫɬɿ; 2) |
||||||||||||||||||||||||||||
ɭɡɚɝɚɥɶɧɸɽɬɶɫɹ ɧɚ ɫɢɫɬɟɦɢ ɪɿɜɧɹɧɶ; 3) ɭɡɚɝɚɥɶɧɸɽɬɶɫɹ ɧɚ ɤɨɦɩɥɟɤɫɧɿ ɤɨɪɟɧɿ. ɇɟɞɨɥɿɤɢ ɦɟɬɨɞɭ ɇɶɸɬɨɧɚ: 1) ɧɚ ɤɨɠɧɿɣ ɿɬɟɪɚɰɿʀ ɨɛɱɢɫɥɸɽɬɶɫɹ ɧɟ
ɬɿɥɶɤɢ f (xk ), ɚ |
ɿ ɩɨɯɿɞɧɚ f (xk ); 2) ɡɛɿɠɧɿɫɬɶ ɡɚɥɟɠɢɬɶ |
ɜɿɞ ɩɨɱɚɬɤɨɜɨɝɨ |
|||||
|
|
|
|
|
|
|
|
ɧɚɛɥɢɠɟɧɧɹ ɯ0, ɬɚɤ ɹɤ ɜɿɞ ɧɶɨɝɨ ɡɚɥɟɠɢɬɶ ɭɦɨɜɚ ɡɛɿɠɧɨɫɬɿ q |
|
M2 |
x0 |
x |
|
||
|
|
|
|
|
1; |
||
|
|
|
|
|
|||
|
f (x) C2 >a,b@. |
|
2m1 |
|
|
|
|
3) ɩɨɬɪɿɛɧɨ, ɳɨɛ |
|
|
|
|
|
|
|
3. Ɇɟɬɨɞɢ ɪɨɡɜ’ɹɡɚɧɧɹ ɫɢɫɬɟɦ ɥɿɧɿɣɧɢɯ ɚɥɝɟɛɪɚʀɱɧɢɯ ɪɿɜɧɹɧɶ (ɋɅȺɊ)
Ɇɟɬɨɞɢ ɪɨɡɜ’ɹɡɭɜɚɧɧɹ ɋɅ Ɋ ɩɨɞɿɥɹɸɬɶɫɹ ɧɚ ɩɪɹɦɿ ɬɚ ɿɬɟɪɚɰɿɣɧɿ. ɉɪɢ
ɭɦɨɜɿ ɬɨɱɧɨɝɨ ɜɢɤɨɧɚɧɧɹ ɨɛɱɢɫɥɟɧɶ ɩɪɹɦɿ ɦɟɬɨɞɢ ɡɚ ɫɤɿɧɱɟɧɭ ɤɿɥɶɤɿɫɬɶ ɨɩɟɪɚɰɿɣ ɜ ɪɟɡɭɥɶɬɚɬɿ ɞɚɸɬɶ ɬɨɱɧɢɣ ɪɨɡɜ’ɹɡɨɤ. ȼɢɤɨɪɢɫɬɨɜɭɸɬɶɫɹ ɜɨɧɢ ɞɥɹ ɧɟɜɟɥɢɤɢɯ ɬɚ ɫɟɪɟɞɧɿɯ ɋɅ Ɋ n=102-104. ȱɬɟɪɚɰɿɣɧɿ ɦɟɬɨɞɢ ɜɢɤɨɪɢɫɬɨɜɭɸɬɶɫɹ ɞɥɹ ɜɟɥɢɤɢɯ ɋɅ Ɋ n>105, ɹɤ ɩɪɚɜɢɥɨ ɪɨɡɪɿɞɠɟɧɢɯ. ȼ ɪɟɡɭɥɶɬɚɬɿ ɨɬɪɢɦɭɽɦɨ ɩɨɫɥɿɞɨɜɧɿɫɬɶ ɧɚɛɥɢɠɟɧɶ, ɹɤɚ ɡɛɿɝɚɽɬɶɫɹ ɞɨ ɪɨɡɜ’ɹɡɤɭ.
3.1. Ɇɟɬɨɞ Ƚɚɭɫɫɚ [ɋȽ, 49-67], [ȻɀɄ, 257-262] |
|
|
Ɋɨɡɝɥɹɧɟɦɨ ɡɚɞɚɱɭ ɪɨɡɜ‘ɹɡɚɧɧɹ ɋɅ |
Ɋ |
|
Ax& |
b , |
(1) |
13

ɩɪɢɱɨɦɭ A (aij )in, j 1,det A 0,x& (xi )in |
1,b (bj )nj |
|
1 . Ɇɟɬɨɞ Ʉɪɚɦɟɪɚ ɡ |
||||||
ɨɛɱɢɫɥɟɧɧɹɦ ɜɢɡɧɚɱɧɢɤɿɜ ɞɥɹ ɬɚɤɨʀ ɫɢɫɬɟɦɢ ɦɚɽ ɫɤɥɚɞɧɿɫɬɶ Q |
O(n!n). |
||||||||
Ɂɚɩɢɲɟɦɨ ɋɅ Ɋ ɭ ɜɢɝɥɹɞɿ |
|
|
|
|
|
|
|
||
|
a11x1 a12 x2 a1n xn |
|
b1 |
|
a1n 1 |
(1’) |
|||
|
® |
|
|
|
|
|
|
|
|
|
°a21x1 a22 x2 a2n xx |
b2 |
a2n 1 |
|
|||||
|
° |
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
°an1x1 an2 x2 ann xn |
bn |
ann 1 |
|
|||||
əɤɳɨ a11 0, ɬɨ ɞɿɥɢɦɨ ɩɟɪɲɟ ɪɿɜɧɹɧɧɹ ɧɚ ɧɶɨɝɨ ɿ ɜɢɤɥɸɱɚɽɦɨ x1 ɡ ɿɧɲɢɯ |
|||||||||
ɪɿɜɧɹɧɶ: |
° |
a12(1) x2 |
a1(1n) xn |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x1 |
|
a1(1n) 1 |
. |
|
|
|||
|
® |
|
a2(1n) xn |
a2(1n) 1 |
|
|
|||
|
° |
a22(1) x2 |
|
|
|
||||
|
° |
|
ann(1) xn |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|||
|
° |
an(12) x2 |
ann(1) 1 |
|
|
|
|||
ɉɪɨɰɟɫ ɩɨɜɬɨɪɸɽɦɨ ɞɥɹ x2 ,..., xn . |
ȼ ɪɟɡɭɥɶɬɚɬɿ |
||
ɬɪɢɤɭɬɧɨɸ ɦɚɬɪɢɰɟɸ |
° |
a12(1) x2 |
a1(1n) xn |
|
|||
|
x1 |
||
|
® |
|
a2(2n) xn |
|
° |
x2 |
|
|
° |
|
|
|
° |
|
xn |
|
¯ |
|
|
ɨɬɪɢɦɭɽɦɨ
a1(1n) 1
a(2)
2n 1 .
a(n) nn 1
ɐɟ ɩɪɹɦɢɣ ɯɿɞ ɦɟɬɨɞɭ Ƚɚɭɫɫɚ. Ɏɨɪɦɭɥɢ ɩɪɹɦɨɝɨ ɯɨɞɭ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
° |
k 1,n |
1: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(k 1) |
|
|
|
|
|
|
|
|
|
||
° |
(k) |
|
akj |
|
|
|
|
|
|
|
|
|
||||
|
, j k 1,n 1; |
|||||||||||||||
°akj |
|
|
|
|
||||||||||||
|
|
(k 1) |
||||||||||||||
® |
|
|
|
|
akk |
|
|
|
|
|
|
|
|
|
||
° |
(k) |
|
|
(k 1) |
|
(k 1) |
(k) |
, |
|
|
|
|
||||
°aij |
aij |
aik |
|
akj |
|
|
|
|
||||||||
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
°i k |
1,n; j k 1,n 1. |
|||||||||||||||
Ɂɜɿɞɫɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
ann(n) 1, xi |
|
ain(i) 1 |
¦aij(i) xj ,i |
|
. |
||||||||||
xn |
|
n 1,1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
j i 1 |
|
|
|
|
|
|
ɫɢɫɬɟɦɭ ɡ
(2)
(3)
ɐɟ ɮɨɪɦɭɥɢ ɨɛɟɪɧɟɧɨɝɨ ɯɨɞɭ.
ɋɤɥɚɞɧɿɫɬɶ, ɬɨɛɬɨ ɤɿɥɶɤɿɫɬɶ ɨɩɟɪɚɰɿɣ, ɹɤɭ ɧɟɨɛɯɿɞɧɨ ɜɢɤɨɧɚɬɢ ɞɥɹ |
||
ɪɟɚɥɿɡɚɰɿʀ ɦɟɬɨɞɭ, - Qɩɪ |
2 |
n3 O(n2 ) ɞɥɹ ɩɪɹɦɨɝɨ ɯɨɞɭ, Qɨɛ n2 O(n) |
ɞɥɹ ɨɛɟɪɧɟɧɨɝɨ ɯɨɞɭ. |
3 |
|
|
|
|
14
|
|
ɍɦɨɜɚ akk(k |
1) |
0 |
|
ɧɟ |
ɫɭɬɬɽɜɚ, |
ɨɫɤɿɥɶɤɢ |
ɡɧɚɣɞɟɬɶɫɹ |
m, ɞɥɹ |
ɹɤɨɝɨ |
|||||||||||||||
|
amk(k 1) |
|
|
|
|
(ɨɫɤɿɥɶɤɢ |
det A |
0 ).Ɍɨɞɿ ɦɿɧɹɽɦɨ |
ɦɿɫɰɹɦɢ |
ɪɹɞɤɢ |
||||||||||||||||
|
max |
aik(k 1) |
|
0 |
|
|||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɧɨɦɟɪɿɜ k ɿ m . ȿɥɟɦɟɧɬ akk(k 1) |
0 ɧɚɡɢɜɚɽɬɶɫɹ ɜɟɞɭɱɢɦ. |
|
|
|
|
|||||||||||||||||||||
|
ȼɜɟɞɟɦɨ ɦɚɬɪɢɰɿ |
|
|
|
|
|
§ |
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
|
|
M |
k |
¨0 |
|
|
m |
kk |
|
|
|
|
¸ , |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
mnk |
|
|
|
|
¸ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
©0 |
|
|
|
1¹ |
|
|
|
||||||||
ɟɥɟɦɟɧɬɢ ɹɤɨʀ ɨɛɱɢɫɥɸɽɬɶɫɹ ɬɚɤ: mkk |
|
|
1 |
|
, |
mkk |
|
|
aik(k 1) |
. |
|
|
||||||||||||||
|
akk(k 1) |
|
|
akk(k 1) |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ɇɟɯɚɣ ɧɚ k –ɦɭ |
ɤɪɨɰɿ |
Ak |
1 x |
|
bk 1 . |
Ɇɧɨɠɢɦɨ |
ɰɸ ɋɅ |
Ɋ ɡɥɿɜɚ |
ɧɚMk : |
||||||||||||||||
|
Mk Ak 1 x Mk bk 1 . ɉɨɡɧɚɱɢɦɨ |
Ak |
|
M k Ak 1 ; |
|
A0 |
A . Ɍɨɞɿ ɩɪɹɦɢɣ ɯɿɞ ɦɟɬɨɞɭ |
|||||||||||||||||||
Ƚɚɭɫɫɚ ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ ɭ ɜɢɝɥɹɞɿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
MnMn 1...M1 Ax |
|
MnMn 1...M1b . |
|
|
|
|||||||||||||||
ɉɨɡɧɚɱɢɦɨ ɨɫɬɚɧɧɸ ɫɢɫɬɟɦɭ, ɹɤɚ ɫɩɿɜɩɚɞɚɽ ɡ (2), ɬɚɤ |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ux |
c , U |
|
(uij )in, j |
1, |
|
|
|
(3) |
||||||||
ɩɪɢɱɨɦɭ |
|
|
|
|
|
|
®uii |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
uij |
|
0,i |
j. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɚɤɢɦ ɱɢɧɨɦ U |
|
Mn M n |
1...M1 A . ȼɜɟɞɟɦɨ ɦɚɬɪɢɰɿ |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
§ |
1 |
|
|
|
0 |
|
|
|
0 |
· |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
L |
k |
M |
1 |
¨ |
0 |
|
|
|
a(k 1) |
|
0¸ . |
|
|
|
||||||
|
|
|
|
|
|
|
|
k |
¨ |
|
|
|
|
kk |
|
|
|
|
|
¸ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
(k 1) |
|
|
|
¸ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
©0 |
|
|
|
ank |
|
|
|
1¹ |
|
|
|
|||||
Ɍɨɞɿ
A L1...LnU LU; L L1...Ln
L- ɧɢɠɧɹ ɬɪɢɤɭɬɧɹ ɦɚɬɪɢɰɹ, U- ɜɟɪɯɧɹ ɬɪɢɤɭɬɧɹ ɦɚɬɪɢɰɹ. Ɍɚɤɢɦ ɱɢɧɨɦ ɦɟɬɨɞ Ƚɚɭɫɫɚ ɦɨɠɧɚ ɬɪɚɤɬɭɜɚɬɢ, ɹɤ ɪɨɡɤɥɚɞ ɦɚɬɪɢɰɿ Ⱥ ɜ ɞɨɛɭɬɨɤ ɞɜɨɯ ɬɪɢɤɭɬɧɢɯ ɦɚɬɪɢɰɶ - (LU) – ɪɨɡɤɥɚɞ
ȼɜɟɞɟɦɨ ɦɚɬɪɢɰɸ ɩɟɪɟɫɬɚɧɨɜɨɤ ɧɚ k -ɦɭ ɤɪɨɰɿ (ɰɟ ɦɚɬɪɢɰɹ, ɨɬɪɢɦɚɧɚ ɡ ɨɞɢɧɢɱɧɨʀ ɦɚɬɪɢɰɿ ɩɟɪɟɫɬɚɧɨɜɤɨɸ k - ɬɨɝɨ ɿ m- ɬɨɝɨ ɪɹɞɤɚ). Ɍɨɞɿ ɩɪɢ ɦɧɨɠɟɧɿ ɧɚ ɧɟʀ ɦɚɬɪɢɰɿ Ak 1 ɪɨɛɢɦɨ ɜɟɞɭɱɢɦ ɟɥɟɦɟɧɬɨɦ ɦɚɤɫɢɦɚɥɶɧɢɣ ɡɚ ɦɨɞɭɥɟɦ.
15

|
§ |
|
|
|
· |
|
|
¨ |
1 |
... |
0 |
¸ |
|
|
¨ . . . |
|
¸ |
|
||
|
¨ |
|
|
|
¸ m k |
|
Pk |
¨ . |
0 |
1 |
¸m m |
|
|
|
¨ . |
1 |
0 |
¸ |
|
|
|
¨ |
|
|
|
¸ |
. |
|
¨0 . . |
. 1 |
¸ |
|||
|
|
|||||
|
© |
|
n |
n |
¹ |
|
|
|
|
|
|
||
|
|
|
k |
m |
|
|
Ɂɚ ɞɨɩɨɦɨɝɨɸ ɰɢɯ ɦɚɬɪɢɰɶ ɩɟɪɟɯɿɞ ɞɨ ɬɪɢɤɭɬɧɨʀ ɫɢɫɬɟɦɢ (3) ɬɟɩɟɪ ɦɚɽ ɜɢɝɥɹɞ:
MnMn 1Pn 1...M1P1Ax& MnMn 1Pn 1...M1P`1b .
Ɍɜɟɪɞɠɟɧɧɹ
Ɂɧɚɣɞɟɬɶɫɹ ɬɚɤɚ ɦɚɬɪɢɰɹ Ɋ - ɩɟɪɟɫɬɚɧɨɜɨɤ, ɳɨ PA LU - ɪɨɡɤɥɚɞ ɦɚɬɪɢɰɿ ɧɚ
ɧɢɠɧɸ ɬɪɢɤɭɬɧɭ ɡ ɧɟɧɭɥɶɨɜɢɦɢ ɞɿɚɝɨɧɚɥɶɧɢɦɢ ɟɥɟɦɟɧɬɚɦɢ ɿ ɜɟɪɯɧɸ
bred!!! |
ɬɪɢɤɭɬɧɭ ɦɚɬɪɢɰɸ ɡ ɨɞɢɧɢɰɹɦɢ ɧɚ ɞɿɚɝɨɧɚɥɿ. |
|
|
|
ȼɢɫɧɨɜɤɢ ɩɪɨ ɩɟɪɟɜɚɝɢ ɬɪɢɤɭɬɧɨɝɨ ɪɨɡɤɥɚɞɭ: |
1.Ɋɨɡɞɿɥɟɧɧɹ ɩɪɹɦɨɝɨ ɿ ɨɛɟɪɧɟɧɨɝɨ ɯɨɞɿɜ ɞɚɽ ɡɦɨɝɭ ɟɤɨɧɨɦɧɨ ɪɨɡɜ‘ɹɡɭɜɚɬɢ ɞɟɤɿɥɶɤɚ ɫɢɫɬɟɦ ɡ ɨɞɧɨɤɨɜɨɸ ɦɚɬɪɢɰɟɸ ɬɚ ɪɿɡɧɢɦɢ ɩɪɚɜɢɦɢ ɱɚɫɬɢɧɚɦɢ.
i v chem + ??? 2. Ɂɛɟɪɿɝɚɧɧɹ M, ɚɛɨ L ɬɚ U ɧɚ ɦɿɫɰɿ Ⱥ.
3.Ɉɛɱɢɫɥɸɸɱɢ l - ɤɿɥɶɤɿɫɬɶ ɩɟɪɟɫɬɚɧɨɜɨɤ, ɦɨɠɧɚ ɜɫɬɚɧɨɜɢɬɢ ɡɧɚɤ ɜɢɡɧɚɱɧɢɤɚ.
3.2.Ɇɟɬɨɞ ɤɜɚɞɪɚɬɧɢɯ ɤɨɪɟɧɿɜ [ɋȽ, 69-73], [ȻɀɄ, 262-263]
ɐɟɣ ɦɟɬɨɞ ɩɪɢɡɧɚɱɟɧɢɣ ɞɥɹ ɪɨɡɜ’ɹɡɚɧɧɹ ɫɢɫɬɟɦ ɪɿɜɧɹɧɶ ɿɡ
ɫɢɦɟɬɪɢɱɧɨɸ ɦɚɬɪɢɰɟɸ
|
|
|
|
|
Ax& b , AT |
|
A. |
|
(1) |
||||
ȼɿɧ ɨɫɧɨɜɚɧɢɣ ɧɚ ɪɨɡɤɥɚɞɿ ɦɚɬɪɢɰɿ Ⱥ ɜ ɞɨɛɭɬɨɤ: |
|
|
|
|
|||||||||
|
|
|
|
|
|
A |
ST DS , |
(2) |
|||||
S – ɜɟɪɯɧɹ ɬɪɢɤɭɬɧɚ ɦɚɬɪɢɰɹ, ST – ɧɢɠɧɹ ɬɪɢɤɭɬɧɚ ɦɚɬɪɢɰɹ, D – ɞɿɚɝɨɧɚɥɶɧɚ |
|||||||||||||
ɦɚɬɪɢɰɹ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
ȼɢɧɢɤɚɽ ɩɢɬɚɧɧɹ: ɹɤ ɨɛɱɢɫɥɢɬɢ S, D ɩɨ ɦɚɬɪɢɰɿ Ⱥ? Ɇɚɽɦɨ |
|
|
|
||||||||||
(DS)ij |
diisij ,i d j |
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯0,i |
j |
|
|
|
|
|
|
|
|
(3) |
||
|
n |
i 1 |
|
|
|
|
n |
||||||
(ST DS)ij |
¦silT dll slj |
¦sliT sljdll |
siisijdii |
sliT ¦sT lisljdll aij ,i, j |
|
|
|
||||||
1,n |
|||||||||||||
|
l |
1 |
l 1 |
|
|
|
l |
i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
əɤɳɨ i = j, ɬɨ |
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
sii2 |
dii |
aii ¦ |
sli2 |
dll |
pi . |
|
|
|
|
Ɍɨɦɭ |
|
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16

|
d ii |
|
sign ( pi ) |
, |
sii |
pi . |
|
||||||||||||||||
əɤɳɨ i j , ɬɨ |
§ |
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
l 1 |
|
|
|
|
|
|
|
|
|
|
i 1,n. |
|
|||||||||
|
© |
|
|
|
|
|
¹ |
|
|
|
|
|
|
|
|
|
|||||||
sij ¨aij |
|
¦sli dll slj |
¸ /(siidii ), i 1,n, j |
|
1. |
||||||||||||||||||
əɤɳɨ Ⱥ>0 (ɬɨɛɬɨ ɝɨɥɨɜɧɿ ɦɿɧɨɪɢ ɦɚɬɪɢɰɿ Ⱥ ɞɨɞɚɬɧɿ), ɬɨ ɜɫɿ dii |
|||||||||||||||||||||||
Ɂɧɚɣɞɟɦɨ ɪɨɡɜ’ɹɡɨɤ ɪɿɜɧɹɧɧɹ (1). ȼɪɚɯɨɜɭɸɱɢ (2), ɦɚɽɦɨ: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
S |
T |
& |
b , |
|
|
|
|
|
|
|
|
|
(4) |
||
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Sx |
y . |
|
|
|
|
|
|
|
|
|
(5) |
||||
Ɉɫɤɿɥɶɤɢ S – ɜɟɪɯɧɹ ɬɪɢɤɭɬɧɚ ɦɚɬɪɢɰɹ, ɚ ST D - ɧɢɠɧɹ ɬɪɢɤɭɬɧɚ ɦɚɬɪɢɰɹ, ɬɨ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bi |
¦sjid jj yj |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
yi |
|
|
|
j |
1 |
|
, |
i |
1,n |
(6) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
nepravilnyj poryadok |
|
|
|
|
|
|
|
siidii |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
yn |
|
|
|
yi |
i¦1sij xj |
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
, x |
|
|
|
j 1 |
, |
i n 1,1. |
(7) |
||||||||||||
|
|
|
s |
|
|
|
|
s |
|||||||||||||||
|
|
n |
nn |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ii |
|
|
|
|
|
|
|
|
|
|
|||
Ɇɟɬɨɞ ɡɚɫɬɨɫɨɜɭɽɬɶɫɹ ɥɢɲɟ ɞɥɹ ɫɢɦɟɬɪɢɱɧɢɯ ɦɚɬɪɢɰɶ. Ƀɨɝɨ ɫɤɥɚɞɧɿɫɬɶ -
Q1 n3 O(n2 ) . ɉɟɪɟɜɚɝɢ ɰɶɨɝɨ ɦɟɬɨɞɭ: 3
1. ɜɿɧ ɜɢɬɪɚɱɚɽ ɜ 2 ɪɚɡɢ ɦɟɧɲɟ ɩɚɦ’ɹɬɿ ɧɿɠ ɦɟɬɨɞ Ƚɚɭɫɫɚ ɞɥɹ ɡɛɟɪɿɝɚɧɧɹ |
|||||
T |
A (ɧɟɨɛɯɿɞɧɢɣ ɨɛ‘ɽɦ ɩɚɦ‘ɹɬɿ |
n(n 1) |
n2 |
||
A |
|
~ |
|
); |
|
|
|
||||
2 2
2.ɦɟɬɨɞ ɨɞɧɨɪɿɞɧɢɣ, ɛɟɡ ɩɟɪɟɫɬɚɧɨɜɨɤ;
3.ɹɤɳɨ ɦɚɬɪɢɰɹ A ɦɚɽ ɛɚɝɚɬɨ ɧɭɥɶɨɜɢɯ ɟɥɟɦɟɧɬɿɜ, ɬɨ ɿ ɜ ɦɚɬɪɢɰɹ S ɬɚɤɨɠ.
Ɉɫɬɚɧɧɹ ɜɥɚɫɬɢɜɿɫɬɶ ɞɚɽ ɟɤɨɧɨɦɿɸ ɜ ɩɚɦ‘ɹɬɿ ɬɚ ɤɿɥɶɤɨɫɬɿ ɚɪɢɮɦɟɬɢɱɧɢɯ
ɨɩɟɪɚɰɿɣ. ɇɚɩɪɢɤɥɚɞ, ɹɤɳɨ A ɦɚɽ m ɧɟɧɭɥɶɨɜɢɯ ɫɬɪɿɱɨɤ ɩɨ ɞɿɚɝɨɧɚɥɿ, ɬɨ
Q O(m2n) .
3.3. Ɉɛɱɢɫɥɟɧɧɹ ɜɢɡɧɚɱɧɢɤɚ ɬɚ ɨɛɟɪɧɟɧɨʀ ɦɚɬɪɢɰɿ [ɋȽ, 67-69]
Ʉɿɥɶɤɿɫɬɶ ɨɩɟɪɚɰɿɣ ɨɛɱɢɫɥɟɧɧɹ ɞɟɬɟɪɦɿɧɚɧɬɭ ɡɚ ɨɡɧɚɱɟɧɧɹɦ - Qdet n!. ȼ
ɦɟɬɨɞɿ Ƚɚɭɫɫɚ - PA |
LU . Ɍɨɦɭ |
|
|
|
|
det LdetU det A |
n |
||
det Pdet A |
( 1)l det LdetU ( 1)l akk(k) , (1) |
|||
|
|
|
|
k 1 |
ɞɟ l - ɤɿɥɶɤɿɫɬɶ ɩɟɪɟɫɬɚɧɨɜɨɤ. əɫɧɨ, ɳɨ ɡɚ ɦɟɬɨɞɨɦ Ƚɚɭɫɫɚ |
||||
|
Qdet |
2 |
n3 |
O(n2 ). |
|
3 |
|||
|
|
|
|
|
|
|
|
|
17 |
ȼ ɦɟɬɨɞɿ ɤɜɚɞɪɚɬɧɨɝɨ ɤɨɪɟɧɹ A=STDS. Ɍɨɦɭ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
det A |
det ST det Ddet S |
|
dkk |
skk2 . |
(2) |
|||||||||||||||
|
|
|
n3 O(n2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|||||
Ɍɟɩɟɪ Qdet |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ɂɚ ɨɡɧɚɱɟɧɧɹɦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
AA 1 |
|
|
E , |
|
|
|
|
|
|
|
(3) |
||||
ɞɟ A 1 ɨɛɟɪɧɟɧɚ ɞɨ ɦɚɬɪɢɰɿ Ⱥ. ɉɨɡɧɚɱɢɦɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
& |
(Dij )in |
|
|
A 1 |
|
|
(Dij )in, j 1 . |
|
|
|
|
|
|
|
|
||||||||||
1 - ɜɟɤɬɨɪ-ɫɬɨɜɩɱɢɤ ɨɛɟɪɧɟɧɨʀ ɦɚɬɪɢɰɿ. Ɂ (3) ɦɚɽɦɨ |
|
||||||||||||||||||||||||
Ɍɨɞɿ D j |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
& |
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
AD j ej |
, j |
|
|
1,n |
|
|
|
|
|
(4) |
||||||||
& |
|
|
|
|
|
|
|
& |
|
|
|
|
n |
|
|
|
|
|
|
|
1,i |
j |
|
||
|
|
|
|
|
|
|
|
|
|
|
1,Gij |
|
|
|
. Ⱦɥɹ ɡɧɚɯɨɞɠɟɧɧɹ |
||||||||||
ej - ɫɬɨɜɩɱɢɤɢ ɨɞɢɧɢɱɧɨʀ ɦɚɬɪɢɰɿ: ej |
(Gij )i |
® |
|
|
|||||||||||||||||||||
i chto dolshe? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯0,i |
j |
|
|||
Ⱥ-1 ɧɟɨɛɯɿɞɧɨ ɪɨɡɜ’ɹɡɚɬɢ n ɫɢɫɬɟɦ . Ⱦɥɹ ɡɧɚɯɨɞɠɟɧɧɹ Ⱥ-1 ɦɟɬɨɞɨɦ Ƚɚɭɫɫɚ |
|||||||||||||||||||||||||
ɧɟɨɛɯɿɞɧɚ ɤɿɥɶɤɿɫɬɶ ɨɩɟɪɚɰɿɣ Q |
2n3 |
O(n2) . |
|
|
|
|
|
|
|
|
|||||||||||||||
3.4. Ɇɟɬɨɞ ɩɪɨɝɨɧɤɢ [ɋȽ, 45-47] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ɐɟ ɟɤɨɧɨɦɧɢɣ ɦɟɬɨɞ ɞɥɹ ɪɨɡɜ‘ɹɡɚɧɧɹ ɋɅ |
Ɋ ɡ ɬɪɢ ɞɿɚɝɨɧɚɥɶɧɨɸ |
|
|||||||||||||||||||||||
ɦɚɬɪɢɰɟɸ: |
|
|
|
|
|
° |
c0 y0 b0 y1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
f0 |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
®ai yi 1 |
|
ci yi |
bi yi 1 |
|
|
|
fi , |
|
|||||||||||
|
|
|
|
|
|
¯ |
|
y |
|
|
c |
|
y |
|
|
|
|
|
f |
|
|
. |
|
|
|
|
|
|
|
|
|
°a |
N |
N |
1 |
N |
N |
|
|
N |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
Ɇɚɬɪɢɰɹ ɫɢɫɬɟɦɢ |
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
§ |
c0 |
|
b1 |
|
|
|
|
|
|
|
0 |
|
· |
|
|
|
|
|||
|
|
|
|
|
¨ |
a0 |
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
A ¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¸ |
|
|
|
|
|
|
|
|
|
|
¨ |
0 |
|
|
|
|
aN |
|
|
|
bN |
¸ |
|
|
|
|
|||||
ɬɪɢɞɿɚɝɨɧɚɥɶɧɚ. |
|
© |
|
|
|
|
|
|
|
|
cN |
¹ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ɋɨɡɜ’ɹɡɨɤ ɩɪɟɞɫɬɚɜɢɦɨ ɭ ɜɢɝɥɹɞɿ |
|
Ei 1,i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Di 1 yi 1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
yi |
|
0,N |
1 |
|
|
(4) |
||||||||||||||
Ɂɚɦɿɧɢɦɨ ɜ (4) i o i 1 ɿ ɩɿɞɫɬɚɜɢɦɨ ɜ (2), ɬɨɞɿ |
|
|
|
|
ai Ei |
|
|||||||||||||||||||
Ɂɜɿɞɫɢ |
|
|
|
|
(aiDi |
ci ) yi bi yi 1 |
|
|
|
|
fi |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18

yi
Ɍɨɦɭ ɡ (5)
Di 1
ɍɦɨɜɚ ɪɨɡɜ‘ɹɡɧɨɫɬɿ (1) ci ɓɨɛ ɡɧɚɣɬɢ ɜɫɿ i ,
|
|
bi |
yi 1 |
fi |
ai i |
||||||||
|
ci |
|
|
aiDi |
ci |
aiDi |
. |
|
|||||
|
bi |
|
|
,Ei 1 |
fi |
ai i |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||
ci aiDi |
|
ci |
aiDi |
,i 1, N 1. |
|||||||||
aiDi |
|
0. |
|
|
|
|
|
|
|
|
|||
i , ɬɪɟɛɚ ɡɚɞɚɬɢ ɩɟɪɲɿ ɡɧɚɱɟɧɧɹ. Ɂ (1): |
|||||||||||||
D1 |
b0 |
, E1 |
|
f0 |
|
(5) |
|||||||
|
|
c |
|||||||||||
|
|
c |
|
|
|
|
|
||||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
ɉɿɫɥɹ ɡɧɚɯɨɞɠɟɧɧɹ ɜɫɿɯ |
i , |
i ɨɛɱɢɫɥɸɽɦɨ yN ɡ ɫɢɫɬɟɦɢ |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aN yN |
cN yN |
|
fN |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ɂɜɿɞɫɢ |
|
|
|
|
|
|
|
|
¯yN 1 |
DN yN |
EN |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fN |
|
aN |
N |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
yN |
cN |
|
aNDN |
. |
|
|
|
(6) |
||||||||||
ɥɝɨɪɢɬɦ |
|
|
|
|
, E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
ɉɨɤɥɚɞɟɦɨ D1 |
|
|
b0 |
|
f0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
c0 |
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
ɉɨɡɧɚɱɢɦɨ zi |
|
ci |
ai |
|
|
|
|
|
|
|
|
|
bi |
fi ai i , ɞɥɹ |
||||||||||||||||
|
i , ɨɛɱɢɫɥɢɦɨ Di 1 |
|
,Ei 1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zi |
|
|
|
zi |
||||||
|
i |
1, N 1 |
|
|
|
aN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
fN |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
Ɂɧɚɣɞɟɦɨ yN |
|
cN |
aNDN |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
Ɉɛɱɢɫɥɸɽɦɨ yi |
|
|
|
i 1 yi 1 |
|
|
|
i 1,i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
N |
1,0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ɋɤɥɚɞɧɿɫɬɶ ɚɥɝɨɪɢɬɦɭ Q |
|
8N |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
Di |
|
t q 1, |
||||||||||||
Ɇɟɬɨɞ ɦɨɠɧɚ ɡɚɫɬɨɫɨɜɭɜɚɬɢ, ɤɨɥɢ ci |
ai |
i |
0 |
i, |
|
1. əɤɳɨ |
|
|
|||||||||||||||||||||||
i |
|
|
|
||||||||||||||||||||||||||||
ɬɨ 'y0 |
t qN 'yN (ɬɭɬ |
'yi |
|
|
|
|
|
|
|
||||||||||||||||||||||
ɚɛɫɨɥɸɬɧɚ ɩɨɯɢɛɤɚ ɨɛɱɢɫɥɟɧɧɹ yi ), ɚ ɰɟ ɩɪɢɜɨɞɢɬɶ |
|||||||||||||||||||||||||||||||
ɞɨ ɟɤɫɩɨɧɟɧɰɿɚɥɶɧɨɝɨ ɧɚɤɨɩɢɱɟɧɧɹ ɩɨɯɢɛɨɤ ɡɚɨɤɪɭɝɥɟɧɧɹ, ɬɨɛɬɨ ɧɟɫɬɿɣɤɨɫɬɿ ɚɥɝɨɪɢɬɦɭ ɩɪɨɝɨɧɤɢ.
Ɍɟɨɪɟɦɚ (ɩɪɨ ɞɨɫɬɚɬɧɿ ɭɦɨɜɢ ɫɬɿɣɤɨɫɬɿ ɦɟɬɨɞɚ ɩɪɨɝɨɧɤɢ).
ɇɟɯɚɣ |
|
i, a0 bN 0 |
||
ai ,bi 0, ɬɚ | ci |t| ai | |
| bi |, |
|||
ɬɚ ɯɨɱɚ ɛɢ ɨɞɧɚ ɧɟɪɿɜɧɿɫɬɶ ɫɬɪɨɝɚ. Ɍɨɞɿ |
|
|
|
|
| i |d1, ɬɚ zi ci |
|
|
|
|
ai i |
0,i 1,N . |
|||
Ɂɚɞɚɱɚ 8 Ⱦɨɜɟɫɬɢ ɬɟɨɪɟɦɭ ɩɪɨ ɫɬɿɣɤɿɫɬɶ ɦɟɬɨɞɭ ɩɪɨɝɨɧɤɢ.
3.5. Ɉɛɭɦɨɜɥɟɧɿɫɬɶ ɫɢɫɬɟɦ ɥɿɧɿɣɧɢɯ ɚɥɝɟɛɪɚʀɱɧɢɯ ɪɿɜɧɹɧɶ [ɋȽ, 74-81], [ȻɀɄ, 303-308]
19

ɇɟɯɚɣ ɡɚɞɚɧɨ ɋɅ Ɋ |
|
Ax& b |
(1) |
ɉɪɢɩɭɫɬɢɦɨ, ɳɨ ɦɚɬɪɢɰɹ ɿ ɩɪɚɜɚ ɱɚɫɬɢɧɚ ɫɢɫɬɟɦɢ ɡɚɞɚɧɿ ɧɟɬɨɱɧɨ ɿ ɮɚɤɬɢɱɧɨ ɪɨɡɜ’ɹɡɭɽɦɨ ɫɢɫɬɟɦɭ
ɞɟ B A C, h& b &, y& x& z&.
By& h |
(2) |
Ɇɚɥɿɫɬɶ ɞɟɬɟɪɦɿɧɚɧɬɭ det A 1 ɧɟ ɽ ɧɟɨɛɯɿɞɧɨɸ ɭɦɨɜɨɸ ɪɿɡɤɨɝɨ ɡɛɿɥɶɲɟɧɧɹ ɩɨɯɢɛɤɢ. ɐɟ ɿɥɸɫɬɪɭɽ ɧɚɫɬɭɩɧɢɣ ɩɪɢɤɥɚɞ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
diag( |
|
|
|
|
|
),aij |
|
|
|
|
|
ij , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Ɍɨɞɿ det A |
n |
1, ɚɥɟ xi |
|
|
|
|
bHi |
. Ɍɨɦɭ 'xi |
|
|
|
Hbi |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ɉɰɿɧɢɦɨ ɩɨɯɢɛɤɭ ɪɨɡɜ’ɹɡɤɭ. ɉɿɞɫɬɚɜɢɜɲɢ ɡɧɚɱɟɧɧɹ B,h ɬɚ z |
y |
x , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɨɬɪɢɦɚɽɦɨ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
(A C)(x& z&) |
b &. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
ȼɿɞɧɿɦɟɦɨ ɜɿɞ ɰɿɽʀ ɪɿɜɧɨɫɬɿ (1) |
Az |
|
Cx |
|
Cz |
|
|
|
. Ɍɨɞɿ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
& |
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
& |
|
|
|
A |
1 |
|
|
& |
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Az |
|
|
K |
|
|
|
Cx Cz, |
|
z |
|
|
|
(K |
|
Cx |
Cz). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ȼɜɟɞɟɦɨ ɧɨɪɦɢ ɜɟɤɬɨɪɿɜ: |
|
|
z& |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z& |
1 |
¦ |
|
z |
i |
, |
|
z& |
2 |
|
|
|
|
( |
¦ |
|
z |
i |
2 ) |
2 |
|
, |
|
z& |
|
|
|
f |
max |
z |
i |
. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||||||||||||||||||||||||
ɇɨɪɦɢ ɦɚɬɪɢɰɿ |
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
, ɳɨ ɜɿɞɩɨɜɿɞɚɸɬɶ ɧɨɪɦɚɦ ɜɟɤɬɨɪɚ, ɬɨɛɬɨ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
sup |
|
|
|
|
Ax& |
|
m |
,m |
|
1,2,f , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
x& |
|
|
|
m |
0 |
|
|
|
|
|
|
x |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɬɚɤɿ: |
|
|
|
A |
1 |
max ¦ |
aij |
|
, |
|
|
|
|
|
|
|
A 2 |
|
max |
|
|
|
|
i (AT A), |
|
|
A |
|
f |
max ¦ |
aij |
, ɞɟ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j 1 |
|
|||||||||
i (B) |
ɜɥɚɫɧɿ ɡɧɚɱɟɧɧɹ ɦɚɬɪɢɰɿ B . |
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ɉɨɡɧɚɱɢɦɨ G(x) |
|
|
|
|
z |
|
, |
G(b) |
|
|
|
|
|
|
|
|
|
, G(A) |
|
|
C |
|
- ɜɿɞɧɨɫɧɿ ɩɨɯɢɛɤɢ x&, b,A, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
A |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɞɟ |
|
|
|
. |
|
|
|
|
|
|
|
. |
|
|
|
k ɨɞɧɚ ɡ ɜɜɟɞɟɧɢɯ ɜɢɳɟ ɧɨɪɦ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Ⱦɥɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɡɜ’ɹɡɤɭ ɦɿɠ ɩɨɯɢɛɤɚɦɢ ɩɪɚɜɨʀ ɱɚɫɬɢɧɢ ɬɚ ɪɨɡɜ’ɹɡɤɭ ɜɜɨɞɹɬɶ ɩɨɧɹɬɬɹ ɨɛɭɦɨɜɥɟɧɨɫɬɿ ɦɚɬɪɢɰɿ ɫɢɫɬɟɦɢ.
ɑɢɫɥɨ ɨɛɭɦɨɜɥɟɧɨɫɬɿ ɦɚɬɪɢɰɿ A - |
cond(A) |
|
|
|
A |
|
|
A 1 |
. |
|
|
|||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɟɨɪɟɦɚ əɤɳɨ A 1 ɬɚ |
|
A 1 |
|
C |
|
1, ɬɨ |
& |
|
||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
condA |
|
|||||||||
|
|
|
G(x&) d |
|
|
|
|
|
|
|
|
(G(A) G(b)), |
(3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 condAG(A) |
|
||||||||||
ɞɟ condA - ɱɢɫɥɨ ɨɛɭɦɨɜɥɟɧɨɫɬɿ.
K
Az& & Cx& Cz&, z& A 1 & A 1Cx& A 1Cz&;
20
