Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теоретична механіка. Відповіді до екзамену

.pdf

Скачиваний:

Добавлен:

19.03.2015

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

является симметрическим волчком. Действительно, каждую главную ось (перпендикулярную к оси симметрии) можно повернуть тогда на угол, отличный от 180°, т. е. выбор этих осей становится неоднозначным, а это возможно лишь в случае симметрического волчка.

Особым случаем является система частиц, расположенных вдоль одной прямой линии. Если выбрать эту прямую в качестве оси xз, то для всех частиц x1 = x2 = 0, и потому

два главных момента инерции совпадают, а третий равен нулю: I1 I2 mx32

, I3 0 .Такую систему называют ротатором. Характерной особенностью ротатора в отличие от общего случая произвольного тела является то, что он имеет всего две (а не три) вращательные степени свободы, соответствующие вращениям вокруг осей x1 и х2; говорить же о вращении прямой вокруг самой себя, очевидно, не имеет смысла.

Наконец, сделаем еще одно замечание по поводу вычисления тензора инерции. Хотя мы определили этот тензор по отношению к системе координат с началом в центре инерции, но для его вычисления может иногда оказаться удобным вычислить


предварительно аналогичный тензор	Iik m(xi ik xi xk )
предварительно аналогичный тензор

Определенный по отношению к другому началу О'. Если расстояние 00' дается

вектором а, то r r a ,			xi xi ai учитывая также,					что mr 0	по
		I		I	(a2	ik	a a )
определению точки О, найдем:		ik		ik		ik	i k
определению точки О, найдем:
По этой формуле, зная Iik	, легко вычислить искомый тензор							Iik .

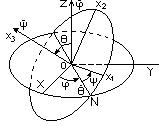
20.Описание поворотов ТТ. Углы Эйлера. Функция Лагранжа ТТ.

Функция Лагранжа ТТ получается из T=1/2* V^2+1/2*Iik i k (см. тензор инерции) вычитанием потен. энергии L=1/2* V^2+1/2*Iik i k-U. Где Iik-тензор инерции - угловая скорость(d /dt= ). Для описания движения ТТ можно пользоваться тремя к- тами его центра инерции и тремя углами определяющих ориентацию осей x1,x2,x3 движущейся СК относительно неподвижной XYZ.В качестве этих углов удобно брать эйлеровы. Начала обеих систем в одной точке. подвижная плоскость х1х2 пересекает неподвижную XY по некоторой прямой ON которую называют линеей узлов.Эта линия перпенд к осям Z и x3.В качестве величин определяющих положение осей х1,х2,х3 отн.осей XYZ примем следующие углы: (teta)-между Z и x3, -между X и N, между N и x1.

и отсчитываются в направл соотв. Правилу правого винта соответствено вокруг осей Z and x3.(0 ).Выразим компоненти угловой скорости по подвижным осям через ейлеровы углы и их производные .Для этого надо спроектировать на эти оси угловые скорости ’, ’, ’: ’-направлена по линии узлов ON и ее составляющие по х1х2х3 равны соответствено: 1’= ’cos , 2’=-’sin , 3’=0.углоавя скорость ’ направлена вдоль Z ее проекция на х3 равна3’= ’cos ,а проекция на х1х2 равна ’sin разлагая последнею по осям х1 и х2 получим: 1’= ’sin sin , 2’= ’sin cos . ’-направлена по оси х3. Собирая все эти составляющие по каждой из осей получим: 1= ’sin sin + ’cos ; 2= ’sin cos ---

’sin ; 3= ’cos + ’.Если оси х1х2х3 выбраны по главным осям инерции то вращательную кинетическую енергию получим подстановкой этих формул в Твр=1 2(I1 1^2+I2 2^2+I3 3^2). Для симметричного волчка Твр=I1/2*( ’^2sin ^2+ ’^2)+I3/2( ’cos + ’)^2.

Примечание: на рисунке величины с точками соответствуют величинам со штрихами в тексте.

21.Динамические уравнения Эйлера для движения ТТ

Пусть dA/dt-скорость изменения какогото вектора А по отношению к неподвижной СК.Если по отношению к вращающейся системе вектор А не изменится то его изменение относительно неподвижной системы обусловлен только вращением и тогда dA/dt=[ A].в общем случае к правой части равенмтва надо добавить скорость изменения вектора А по отношению к подвижной СК;обозначив эту скорость d’A/dt имеем dA/dt=d’A/dt+[ A].С помощю этой формулы мы можем переписать уравнения движения ТТ dP/dt=F and dM/dt=K в виде d’P/dt+[ P]=F and d’M/dt+[ M]=K

Поскольку диф-ние по t производится в подвижной СК то можно спроецировать уравнения на оси этой СК:(d’P/dt)1=dP1/dt, …,(d’M/dt)1=dM1/dt, …,где индексы 1 2 3

означают комп.по осям х1х2х3

При этом в первом ур-ии заменяем Р на V : (dV1/dt+ 2V3-

3V2)=F1; (dV2/dt+ 3V11V3)=F2 (dV3/dt+ 1V22V1)=F3,Предполагая оси х1х2х3 выбраными по главным осям инерции пишем во втором уравнении (с

моментом и К) M1=I1 1 и т.д. и получаем:I1*d 1/dt+(I3-I2) 2 3=K1 I2*d 2/dt+(I1I3) 3 1=K2;I3d 3/dt+(I2-I1) 1 2=K3-Эти уравнения называют уравнениями Эйлера

22. Свободное движение симметрического и шарового волчков. Что можно сказать о движении асимметрического волчка? Кинетическая энергия, выраженная через тензор

T	V 2	1	Iik i			2
	2	2		где	Iik m xl ik xi xk
							–тензор инерции

	m(y
	m(y

Iik

2 z2)

myx mzx

mxy				mxz
mxy				mxz
m(x	2	2	)	myz
m(x		z	)	myz					Приводя тензор инерции к диагональному виде
mzy				m(x	2	y	2		Приводя тензор инерции к диагональному виде
mzy				m(x		y		)

путѐм выбора новых осей x1, x2, x3, тогда I1,I2,I3 –главные моменты инерции. За определением I1=I2=I3 –Шаровой волчок, в этом случае можно выбирать любые главные оси инерции. I1=I2 I3 –симметричный волчок, в этом случае в плоскости x1,x2 можно выбирать любые главные моменты инерции. I1 I2 I3Асимметричный волчок. Для асимметричного волчка можно записать интегралы уравнения Эйлера.

* 2

Эти уравнения представляют собой

геометрический эллипсоид, и выполняется неравенство 2EI1<M2<2EI3. Вращение вокруг осей x1 x3 устойчиво, а вокруг оси x2 нет. При M2=2EI3 тогда 1 2 0

3 const т.е. вектор омега постоянно вращается вдоль ось инерции x3. Аналогично при M2=2EI1 – равномерное вращение вокруг оси x1.

23.Функция Лагранжа для одной частицы в инерц. системе отсчета.

L ( mv02 ) U
0	2	Рассмотрим систему k‘ которая движется относительно системы k0 со

скоростью V(t). V0 – скорость в системе k0, а v’ – в системе k’. Эти скорости связанны

	V0 V' V(t)		L'	mv'2	mv'V (	m	)V2	U
между собой соотношением		и		2		2			Заменяя

v’=dr’/dt, где dr- радиус-вектор в системе k’ тогда

mV(t)v' mV(		dr'	)		d	(mVr ' ) mr ' (	dV	)
mV(t)v' mV(		dt	)		dt	(mVr ' ) mr ' (	dt	)
		dt			dt		dt	Заменяя W(t)=dV/dt. Тогда фун-
L'	mV'2			mW(t)r'U
L'	2			mW(t)r'U
ю Лагранжа	2

Вводя новую систему К которая имеет общее с системой К’ начало и вращается с угловой скоростью омега(t). Скорость v’ складывается со скорости v относительно системы К и со скорости вращения [омега*r] вместе с системой К’, тогда

v' v [ r ] L	mv2	mv[ r ]	m[ r ]2	mWr U

2		2		Это общий вид

функции Лагранжа частици в произвольной неинерциальной системе отсчѐта. Рассмотрим особый случай, когда омега=const и W=0 то

	MV	2	2			m[ r ]2
L (			) MV[ r ]	m[ r ]	U
						2 - дополнительная потенциальная
	2		2

энергия (центробежная).

24. Рассеяние. Сечение рассеяния. Решим сначала задачу об отклонении частицы массой m в поле U(r) неподвижного силового центра расположенного в центре инерции частиц. Траектория частицы в центральном поле симметрична по отношению к прямой проведенной в ближайшую к центру точку орбиты ОА. Поэтому обе асимптоты пересекают эту прямую под одинаковыми углами

нии мимо центра есть, как видно из рисунка,

					M	dr
					r 2	dr
					r 2

				2m E U r			M2
χ	π 2	. Угол определяется интегралом	rm i n				M2	(1) где rmin
χ	π 2						r 2

корень подрадикального выражения. Введем величины -прицельное расстояние на котором бы прошла частица мимо центра, если бы силовое поле отсутствовало, v - скорость частицы на бесконечности, тогда E=(m v 2)/2, M=m v и

r 2

rm i n

(2) , определяющая

зависимость от .

Рассеяние пучка. dN-число частиц пучка рассеиваемых за единицу времени на углы лежащие в интервале и +d , n-число частиц, проходящих в единицу времени через единицу площади поперечного сечения пучка (пучок однороден), =dN/n – эффективное сечение рассеяния, которое полностью определяется видом рассеивающего поля. В заданный интервал углов будут рассеиваться частицы, летящие с прицельного расстояния между ( ) и ( )+d ( ). Число таких частиц dN=2 d n, тогда d =2 d . Зависимость эффективного сечения от угла рассеивания

d 2	d	d	d		d	d


				sin	d
	d
		(3) или через телесный угол				, где

d 2 sin d

. Формула (3) определяет эффективное сечение в зависимости от угла рассеивания в системе центра инерции. Для нахождения эффективного сечения в зависимости от угла рассеивания в лабораторной системе надо выразить через . Угол рассеивания падающего пучка

tg 1		m2 sin
	m1	m2 cos , угол рассеивания первоначально покоившихся частиц

2=( - )/2

25. Формула Резерфорда. (Сечение рассеяния см. ответ 24).

Рассмотрим рассеяние частиц в поле U=/r (кулоновское). Подставим это в формулу

(2) ответа 24 и производя ЭЛЕМЕНТАРНОЕ интегрирование, получим

arccos		mv 2
						2	2		2	2 4	2 2	2 4
				2

			2		откуда			tg		m v	ctg	m v	, где
			2					tg		m v	ctg	m v
	1		mv								2

=( -)/2. Дифференцируя это выражение по и подставляя в (3) ответа 24, получим

			2	c os				2
			2	c os				2	d
d				2	d				d
d		2		3	d		2		4
	mv			s in		2mv			s in	- формула Резерфорда
	mv			s in		2mv			s in
				2					2
				2					2

в системе покоящегося центра инерции сталкивающихся частиц. Преобразование к лабораторной системе производится с помощью двух последних формул ответа 24, там

			2	d 2
d 2				d 2
d 2		2		3	2
где 1 и 2 выражаются через . Получим	mv			cos	2	- сечение рассеяния

покоящихся частиц. Для налетающих частиц имеем два случая и трѐх телок : 1)

d 1

m2>m1

4E1

sin4

где

mv2 / 2

- энергия падающей частицы. 2)

cos 1

d 1

m1=m2

. Если частицы тождественны, общее эффективное

sin

cos d

сечение

sin

cos

. Энергия, теряемая

2m v sin

налетающей частицей m1

при соударении равна

где

m=m1m2/(m1+m2) – приведенная масса. Тогда эффективное сечение как функция от

	d	2 2d
потери энергии:	d	m v2 2	где пробегает значения от 0 до
		m v2 2
		2

max 2m2v2 m2

26.Полный дифференциал ф-и Лагранжа (ф-я координат и скоростей): По

dqi

dqi dL pidqi

pidqi .

сле простейших преобразований

получаем:

d( piqi

L) pidqi qidpi

Величина в скобках - полная энергия системы

H(pi

,qi ,t) piqi L(q,q,t)

ф-я Гамильтона (через координаты и импульсы):

.Из

дифференциального равенства:

dH pidqi

qidpi qi

, pi

Это искомые ур-я движения в

переменных p и q

L E.

Также можно написать: i

Канонические преобразования –это

преобразования координат импульса, которые допускается в формализма Гамильтона:

	К.п. допускают преоб. коорд.qi и pi без изменения ур-й Гамильтона. Новые
ra qi(t)
					H		H
координаты: Qi=Qi (pi,q,t) и Pi=Pi(p.q,t)				Qi	Pi	, gdePi	.......
					Pi		Qi
		d
PiQi H (P,Q,t)			F(qi,pi,Qi ,Pi,,t)
PiQi H (P,Q,t)		dt	F(qi,pi,Qi ,Pi,,t)
i		dt
i

Если задать такую ф-ю :F=Fдругюобозню(qi,Qi,t) ,то можно получить преобразования:

pi	F	pi	F	F qiQi
	qi и
			Qi .Пусть ф-я		из нее можно получить :Pi=-
			Qi .Пусть ф-я	i	из нее можно получить :Pi=-
			F (Pi ,qi ,t) Pi		F

					i Значить можно написать Ф в
qi,Qi=pi.С другой стороны					i Значить можно написать Ф в

PiQi F(q,Q,t)

виде: i преобраз. Лежандра. Полный диффер.:

{PidQi QidPi

dqi

dQi }

Pi и

qi .

H H

t Ф-я Ф может быть

27.Уравнения Гамильтона как следствие вариационного принципа.

С помощью принципа Гамильтона можно найти вариационный принцип который

I Ldt 0

приводит к тем же уравнениям :

Подставив ф-ю Лагранжа,

H(q, p,t)dt 0

I ( pi qi

выраженую через гамильтониан получим:

pi qi

Hdt 0

модифицированный принцип Гамильтона или

Запишем

(

-вариация интеграла):

м.п.Гам. с помощью параметра

,где

d d

[ pi qi

H(q, p,t)]dt 0

t1 i

или можно записать:

H pi

d (

qi pi

)dt 0

( t1,t2 ).Можна заменить

(*)

dt (

) ->

на

d qi

dt pi

.Так как

q ,d

i можна равенство (*) переписать в виде:

[ pi (qi

) qi (pi

)]dt 0

,но так как вариации qi и

pi являются

независимыми, то этот интеграл может обращаться в 0 тогда, когда равны 0

коэффициенты при вариациях. Следовательно ебаные равенства:

, pi

qi совпадают с уравнениями Гамильтона

28. Уравнения Рауса

Преобразование, с помощью которого из уравнений Лагранжа получены уравнения Гамильтона, Называется преобразованием Лежандра (это преобразование широко используется в Теор. Физике)Используя преобразование Лежандра, получим уравнения Рауса, т.е. уравнения движения которые относительно одной части переменных имеют вид уравнений Лагранжа, а относительно другой части переменных – вид уравнения Гамильтона. Действительно возьмем переменные

t,qi ,qi (i 1,2...,

m),qa, pa(a m 1,...,

s;m s)

и введем функцию

этих переменных -- функцию Раусса

q,q ,q

, p,t

Рассматривая Дифференциалы

a m 1

1 m

этой функции приходим к уравнениям Раусса

Qi ;(i 1,2...,

, pa

Qa ; i

1,2,...,

если все координаты

qa a m 1,...,

являются циклическими

Qd 0

координатами, а все

То функция Раусса будет иметь вид

R R q1,..., qm;q1,...,

qm; pm 1,0,...,

ps,0

Поскольку справедливы

a m 1,..., s

соотношения

постоянны

а импульсы

Таким образом в этом случае задача сводится к решению задачи Лагранжа

относительно координат q1,..., qm; P.S. : Выражение для энергии через функцию Раусса имеет вид

	L		L		L		R
E q		qj		L pq qj		L;E R qj
E q		qj		L pq qj		L;E R qj
	q		qj		qj		qj

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.09.201947.71 Кб2теорія.docx
#
31.08.201968.65 Кб0теорія.docx
#
08.09.201923.62 Кб0теорія.docx
#
10.09.201946.97 Кб1теорія.docx
#
07.05.2019249.34 Кб1Теоретичні проблеми циві. права.[1].doc
#
19.03.20151.17 Mб27Теоретична механіка. Відповіді до екзамену.pdf
#
07.03.2016202.75 Кб29теоретична частина.doc
#
12.11.2019125.95 Кб0Теоретичний матеріал.doc
#
12.11.2019512.51 Кб1Теоретичний матеріал_з посібника Коваленко Ю.О....doc
#
19.03.2015283.65 Кб56Теория МО для КР новая 2014.doc
#
17.04.2019292.87 Кб12теория ответы 1-60.docx