OFP-Tretyak-Lozovski

Отже відносна зміна енергії електрона за розсіювання на акустичних коливаннях ґратки складає за порядком величини відношення швидкості звуку в кристалі до швидкості електрона. Швидкість звуку в

кристалі cs 105 cм c–1, а швидкість електронів за кімнатної температури V 107 cм c–1, що дає

Таким чином, процеси розсіювання електронів на коливаннях ґратки за кімнатної температури можна з великою точністю вважати пружними. За низьких температур, коли швидкість електронів у валентній зоні є малою, відносна зміна енергії електрона за розсіювання на коливаннях ґратки матиме порядок величини енергії фонона.

Крім подібних процесів розсіювання можуть відбуватися переходи електронів між виродженими мінімумами у зоні провідності. Такі процеси називаються міждолинним розсіюванням.

6.7. Задачі

1.В яких напівпровідниках існують, крім акустичних, оптичні гілки коливань ґратки

– Si, Ge, GaAs, InSb?

2.Розгляньте лінійний ланцюжок атомів із виходом за межі врахування взаємодії тільки між атомами – найближчими сусідами. Вважайте, що пружну силу, яка діє на

n-й атом, можна записати у вигляді

де un = u(na), а – стала ґратки (порівн. із (6.1)). Покажіть, що закон дисперсії коливань ґратки тепер має вигляд

3. Знайдіть закон дисперсії довгохвильових коливань одновимірного одноатомного ланцюжка атомів у наближенні із попередньої задачі, і за припущення, що

βp = Ap–γ. Зокрема, розгляньте випадки 1 < γ < 3, γ = 3 та γ = 1.

Указівка. У цьому випадку ряд під коренем (6.78) розходиться, що не дає м о- жливості скористатися розкладенням синуса, але завдяки малим значенням хвильового числа k можна перейти від підсумовування до інтегрування.

Розділ 7 ДОМІШКИ ТА ДЕФЕКТИ

ВНАПІВПРОВІДНИКАХ

Упопередніх розділах ми розглянули основні ідеї зонної теорії ідеаль- них кристалів, усі вузли ґратки (що безперервно простягаються в усіх напрямках) яких заповнені тільки атомами певної речовини. Однак існуючі технології не надають можливості отримання ідеального кристала. Усі кристали тією чи іншою мірою характеризуються різноманітними недосконалостями, що викривляють строгу періодичність ідеальної ґратки. Крім того, домішки та дефекти у напівпровідниках відіграють вирішальну, а часто й фатальну роль у формуванні їхніх властивостей. Наприклад, один з авторів (О.В.Т.) у 80-х роках був учасником такого повчального випадку. Під час державного приймання новозбудованого заводу для автоматизованого виробництва МОП інтегральних схем як вихідний матеріал використовувались кремнієві пластини виробництва однієї із західноєвропейських фірм. Після проходження всього технологічного ланцюжка, що включав кілька десятків операцій, вихід стандартної продукції складав близько 70 %, що відповідало всім тогочасним нормам. За спроби використати як вихідний матеріал кремнієві пластини вітчизняного виробництва, що за

паспортом (тип провідності, концентрація домішок 1015cм–3, концентрація дислокацій) точно відповідали іноземному аналогу, відсоток стандартної продукції ледь досяг кількох одиниць. Вивчення причин такої ситуації показало, що вітчизняні кремнієві пластини характеризувались концентрацією неконтрольованих домішок, на порядок

вищою ( 1012 – 1013 cм–3 ) за європейський аналог ( 1010 – 1011 cм–3). Технологічний цикл виробництва мікросхем містив процес відпалю-

вання за температур 700 0С. Виявилося, що за таких температур неконтрольовані дефекти призводили до значного зростання концентрації дислокацій та інших дефектів (т. зв. глибоких центрів). І якщо зростання концентрації таких дефектів в іноземному зразку не в и- кликало фатальних наслідків, то на порядок вища концентрація неконтрольованих дефектів у вітчизняному – призводила до повної непридатності запропонованої технології для виготовлення інтегральних схем на базі вітчизняного кремнію. На щастя з'ясувалось, що зниження температури відпалювання на кілька десятків градусів, що припускалось технологічними умовами, не викликало значного зростання концентрації неконтрольованих дефектів. У результаті виробництво мікросхем на вітчизняній базі виявилось успішним. Цей випадок свідчить про суттєву роль домішок і дефектів у фізиці напівпровідників та є одним із прикладів, що спонукають зважати на наявність недосконалостей напівпровідникових кристалів.

Таким чином, питання про роль дефектів і домішок у твердому тілі, зокрема у напівпровідниках, виявилось основним у процесі впровадження напівпровідникових технологій. Фактично відповіді на це питання були присвячені основні зусилля науковців, які протягом десятків років розвивали науку й технологію напівпровідників. Більш того, можна стверджувати, що завдяки вмінню керувати властивостями домішок і дефектів у напівпровідниках і виникла сучасна напівпровідникова електроніка.

Зрозуміло, що існування домішок вплине на формування характеристик кристала, отже приведе до відмінності його властивостей від властивостей ідеального кристала. Перед аналізом впливу дефектів на електронні властивості напівпровідника коротко розглянемо класифікацію дефектів кристалічної ґратки.

В умовах термодинамічної рівноваги навіть в ідеальному кристалі існують відхилення від точного розташування атомів у вузлах ґратки Браве. Такі відхилення називаються дефектами кристалічної ґратки. Рівноважні дефекти – це такі дефекти кристала, що є елементарними збудженнями основного стану кристала. До цього типу дефектів належать фонони – колективні коливання атомів кристалічної ґратки. У реальних кристалах, крім рівноважних дефектів ґратки, існують нерівноважні дефекти, викликані переважним чином неідеальними умовами росту та існування кристала. Часто нерівноважні дефекти кристалічної ґратки стабілізуються електричними, магнітними або пружними полями, що виникають у кристалі під час його росту, фазових перетворень або зовнішніх дій, наприклад радіаційного опромінювання. Таким чином з'являється можливість суттєвого зменшення густини нерівноважних дефектів за рахунок удосконалення методів вирощування та обробки кристалів.

Можливість існування дефектів із великою енергією утворення в умовах термодинамічної рівноваги за температури Т можна пояснити тим, що утворення дефектів викликає збільшення ентропії кристала у цілому щодо ідеального кристала. Нехай кристал має N однакових атомів, і в ньому утворюються n вакансій. Видалити із кристала, що містить N атомів, n атомів, і тим самим утворити n вакансій можна

способами. Тоді, згідно із формулою Больцмана, відповідне збільшення ентропії кристала виражатиметься величиною

вання атомів у вузлах переривається точковим або протяжним дефектом: точкові дефекти зазвичай пов'язуються з окремими атомами в локальних областях кристала; протяжні – можна поділити на лінійні (одновимірні) та двовимірні (поверхневі). У цьому сенсі й пов ерхню, якою закінчується кристал, можна розглядати як двовимірний дефект. До двовимірних дефектів також можна зарахувати межі розподілу різ- них фаз, межі блоків, зерен, доменів тощо. До тривимірних дефектів належать пори, включення тощо.

Точкові дефекти додатково класифікують таким чином:

вакансія – дефект, викликаний відсутністю атома у вузлі;

атом у міжвузлів'ї – дефект, обумовлений атомом (власної речовини або домішки), що займає місце між вузлами ґратки;

атом заміщення – дефект, за якого атом домішки заміщує атом власної речовини у вузлі;

антисайт – особливий тип дефекту заміщення, за якого власний атом А у сполуці займає місце іншого власного атома В;

дефект Френкеля, який розглядають як точковий, що являє собою комплекс із вакансії та міжвузлів'я, тобто власний атом, зсунутий із вузла в напрямку найближчого міжвузлів'я.

Вакансії та антисайти є власними дефектами, що не пов'язані з наявністю сторонніх атомів у кристалі. Їхню концентрацію не можна визначити методами хімічного аналізу або мас-спектрометрії. Вони не

єелектрично активними і не викликають зміни концентрації носіїв. Але контролювання таких дефектів є дуже важливим, оскільки вони можуть визначати поведінку кристалів під час різноманітних технологічних операцій. Тому під час вирощування кристалів прагнуть домогтися, щоб концентрація таких дефектів не перебільшувала величину

1010–1012 cм–3.

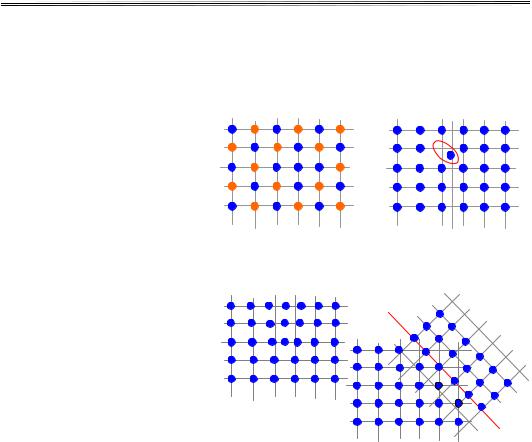
Рис. 7.1. Точкові дефекти: а – вакансія; б – атом заміщення; в – атом у міжвузлів'ї

Схематично точкові дефекти подано на pис. 7.1 та 7.2. Схеми не показують процес релаксації ґратки в околі дефекту, хоча зрозуміло, що в невеликому околі дефекту ґратка зазнає деяких дефо рмацій, і недосконалості насправді займають великі ділянки ґратки. Характерним

зовані на домішкових рівнях, можуть лежати всередині забороненої зони та мати однакову величину для домішок одного типу. Дійсно, наявність домішок означає, що, крім кристалічного потенціалу, на електрон у кристалі діє потенціал, обумовлений сильним локальним збуренням поля домішки. Розглянемо загальну задачу про електрон у кристалі, на який накладено сильне локальне збурення. Нехай поле

цього збурення локалізоване в області із центром у точці Ri − W(r − Ri). Рух електрона в такому випадку описується рівнянням Шредингера

Припустимо, що розв'язок цього рівняння для ідеального кристала, де W(r − Ri) = 0, відомий. Розкладемо невідому хвильову функцію в (7.9) за блохівськими функціями ідеального кристала

Подіємо на це рівняння оператором Ik′ = ∫dr(ψk′(r))* .... Із врахуванням

ортонормованості хвильових функцій ідеального кристала ψk(r) отримаємо рівняння для визначення коефіцієнтів розкладання (7.10)

Оскільки збурення є малим усюди, крім малої областіVR в околі точки Ri, то інтегрування при обчисленні матричних елементів Wk'k можна проводити за малим об'ємом із центром у точці Ri:

R VR

– середнє значення енергії за об'ємом VR. Суттєвим є те, що ця величина не залежить від координати точки Ri локалізації дефекту. Підс-

тавимо (7.13) до (7.12)