
s2_matan_kol_shpore_html_pdf
.pdf
#31
Інтеграли Ейлера: Г(а), В(а,в) – області збіжності та рівномірної збіжності.
|
x s |
(2) |
|
||
s |
1e x dx , |
|
|||
|
0 |
|
|
|
|
В околі нуля e x xs 1 |
0 xs 1 , тому збігається, коли s 0 ,а I 2 s збігається s 0 |
s |
|||
існує при s 0 . |
|
|
|
|
|
Якщо розглянути s : 0 s |
s |
s |
2 |
, то e x xs |
1 |
e x |
x s0 1 xs1 1 |
, |
а інтеграл від |
1 |
|
|
|
|
|
|
|
|
|
функції в правій частині останньої |
|
рівності існує, |
то |
s |
рівномірно |
збігається на |
|||
розглянутому проміжку, тобто |
s |
є неперервною на будь-якому додатному сегменті |
|||||||
s1 , s2 , в наслідок довільності s1 |
та s2 |
будемо мати, що |
|
s неперервна |
s |
0 . |
|||
(1)
|
1 |
B p, q |
x p 1 1 x q 1 dx |
|
0 |
Коли x 0 x p 1 1 x q 1 |
0 |
x p 1 |
збіжний при p 0 і коли x 1 |
||||
x p 1 1 x q 1 |
0 1 x q 1 |
збіжний при q |
0 . З цього слідує, що B p, q існує у |
||||
відкритому квадранті p, q . Взявши довільні p0 |
0 , q0 0 і розглянувши область p p0 , |
||||||
q q0 одержимо, що x p 1 1 |
|
x q 1 |
x p0 |
1 1 |
x q0 1 , тобто інтеграл (1) збігається |
||
рівномірно, з чого слідує неперервність B |
p, q |
0 . |
|||||

#32
Інтеграли Ейлера: Г(а) – формула пониження.
s x s 1e x dx
0
s 1 |
x s e x dx |
x s e x |
|
s x s 1e x dx s |
(4) |
0 |
s |
||||
|
0 |
|
0 |
|

#33
Інтеграли Ейлера: В(а,в) – симетрія, формула пониження.
1
B p, q  x p 1 1 x q 1 dx
x p 1 1 x q 1 dx
0
1.(Симетрія |
B p, q |
B q, p - доведення через заміну (y |
(8) |
|||||||||||||
) |
= 1-x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.(Формула |
p 0, q 1 B p, q |
|
|
q |
1 |
B p, q 1 |
|
|
|
(9) |
||||||
пониження |
|
p q 1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доведення. |
|
1 |
|
|
p |
p |
|
|
q 1 |
|
1 |
q 1 |
1 |
|
||
|
|
|
|
|
|
|
||||||||||
B p, q |
1 x q 1 d |
x |
|
|
x 1 |
x |
|
|
x p 1 |
x q 2 dx |
||||||
|
|
|
|
|
||||||||||||
|
p |
|
|
p |
|
|
|
0 |
p |
|
||||||
|
|
0 |
|
|
|
|
|
0 |
|
|||||||
q 1
p
1
x p 1 1 x q 2 |
x p 1 1 x q 1 dx |
0
|
|
q |
1 |
B p, q |
1 |
|
q 1 |
B p, q |
(9) |
|
|
|
|
|
|
||||||
|
|
p |
|
|
|
|
|
p |
|
|
Аналогічно |
|
p 1, q |
0 |
має місце. |
|
|||||
B p, q |
|
p |
1 |
B p 1, q |
(10) |
|||||
p q 1 |
|
|||||||||

#34. Різні формули запису для B(a,b).
1
B(a,b) xa 1 (1 x)b 1 dx
- бета функція Ейлера
0
B(a, b) |
|
Г (а) Г (b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Г (a |
|
b) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
xa 1 (1 x)b 1 dx |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
t |
|
|
|
|
t a 1 |
1 |
|
|
|
|
|
dt |
|
|
|
|
|
|
t a 1dt |
|
|||||||||||||||||
B(a, b) |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||
|
|
|
1 t |
|
|
1 t |
(1 t)a 1 (1 t)b 1 |
|
(1 t)2 |
|
|
(1 t)a b |
|||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
dt |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(1 |
t)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
;1 x 1 |
1 |
1 t |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
xa 1 |
1 |
xa 1 |
|
|
|
|
|
|
|
|
xa 1 |
|
|
|
|
|
|
|
t |
|
|
|
t |
|
|
|
||||||||||||||||||||||
B(a, b) |
|
|
|
|
dx |
|
dx |
|
|
|
dx |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
(1 x)a b |
(1 x)a b |
|
(1 x)a b |
|
|
|
|
dx |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
xa 1 |
|
|
|
0 |
|
ta b |
|
|
|
|
dt |
1 |
|
|
|
xa 1 |
|
1 |
|
|
tb 1 |
|
|
|
|
|
1 xa 1 |
|
xb 1 |
|
||||||||||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dt |
|
|
|
|
|
|
dx |
|
|||||||||||||||||||||||||||
0 |
(1 x)a b |
ta 1 (1 t)a b |
|
|
|
t 2 |
0 |
|
(1 x)a b |
0 |
(1 t)a b |
0 |
|
(1 x)a b |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

#35. Зв’язок між В(а,в) та Г(а).
B(a, b) |
|
|
|
Г (a)Г (b) |
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Г (a b) |
|
|
|
|
|
|
|
|
|
|
|
|||
Доведення : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Г (a) |
|
xa 1e x dx |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
(q |
1)t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Г (a |
b) |
|
|
|
|
xa |
b 1e x dx |
q |
параметр |
|
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
dx |
(q |
1)dt |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Г (a b) (q 1) (q 1)a b 1t a b 1e(q 1)t dt |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Г (a b) |
|
|
|
t a b 1e (q 1)t dt * qa 1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
(q 1)a b |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
qa |
1 |
|
Г (a b) |
|
|
|
qa 1ta b 1e (q 1)t dt |
|
|
|
|||||||||
(1 q)a b |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Г (a b) |
|
|
|
|
qa |
1dq |
|
|
|
|
dq qa 1t a b 1e(q 1)t dt |
tb 1e t dt qa 1t ae qt dq |
|||||||
|
|
|
(1 |
q)a |
b |
|
|||||||||||||
|
|
0 |
0 |
|
0 |
|
|
0 |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
tb 1e t dt (qt)a 1 e qt d (tq) |
tb 1e t dt ya 1e y dy Г (a)Г (b) |
||||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
||
Г (a b)B(a b) |
Г (a)Г (b) |
B(a, b) |
Г (a)Г (b) |
||||||||||||||||
|
|
|
|||||||||||||||||
Г (a |
b) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

#36. Інтеграли Ейлера: формула доповнення.
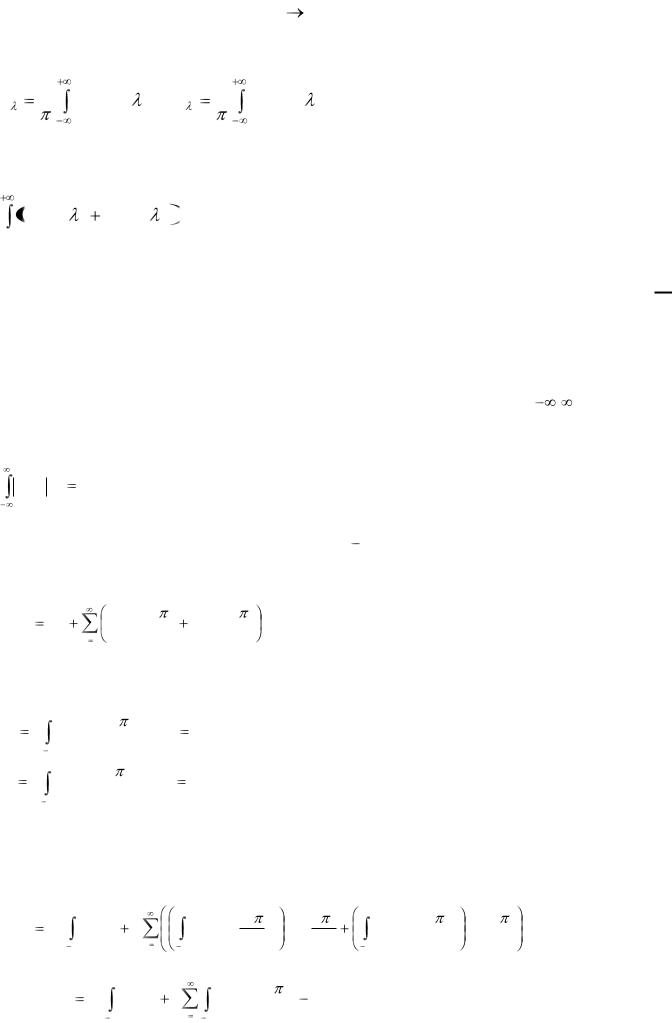
#37_1
Поняття: Якщо для функції f : R R функції a , b
, b обчислюються за формулами
обчислюються за формулами
a |
1 |
f (t) cos tdt , b |
1 |
f (t) sin tdt , |
(1) |
|
|
||||
|
|
то тригонометричний інтеграл
a cos x b
cos x b sin x d
sin x d
0
називається інтегралом Фур’є (або повторним інтегралом Фур’є) функції f .
Означення: Нехай функція f (x) визначена на всій числовій прямій та задовольняє таким умовам:
Функція f (x) є обмеженою та абсолютно інтегрованою на ( ; ) , тобто існує невластний інтеграл
f (x) dx Q 
2. У будь-якому скінченому проміжку [ l, l]функція f (x) розкладається у ряд Фур’ є
f (x) |
a0 |
|
an cos |
n |
x |
bn sin |
n |
x |
(2.1) |
2 |
n 1 |
|
l |
l |
|
де коефіцієнти Фур’є визначаються формулами
an |
1 l |
f (x) cos |
n x |
dx; |
n |
0,1,2,... |
||||
l |
|
|
l |
|
||||||
|
l |
|
|
|
|
|
(2.2) |
|||
|
1 l |
|
|
n x |
|
|
|
|||
b |
|
f (x) sin |
dx; |
n |
1,2,3,.. |
|||||
|
|
|
|
|
||||||
n |
l |
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||
Підставивши замість коефіцієнтів an і bn їх вирази, перепишемо ряд у вигляді
f (x) |
1 |
l |
f (t)dt |
1 |
l |
||
|
|
|
|
|
|
||
2l |
l |
|
l n 1 |
l |
|||
|
|
|
|||||
f (t) cos ntl dt cos nl x
l
l
f (t) sin |
nt |
dt sin |
n x |
|
l |
l |
|||
|
|
Або |
f (x) |
1 l |
f (t)dt |
1 |
||
|
|
|
|
|||
2l l |
|
l |
||||
|
|
|
|
|||
l
n 1 l
f (t) cos |
n |
(t x)dt (2.3) |
|
l |
|||
|
|
Достатні ознаки розкладності функції в ряд Фур'є
Крапка розриву функції називають крапкою розриву першого роду, якщо існують кінцеві межі праворуч і ліворуч цієї функції в даній крапці.
ТЕОРЕМА 1 (Дирихле). Якщо періодична з періодом функція безперервна або має кінцеве число крапок розриву 1-ого роду на відрізку * + і цей відрізок можна розбити на кінцеве число частин, у кожному з яких f(x) монотонна, то ряд Фур'є щодо функції сходиться до f(x) у крапках безперервності й до среднеарифметическому однобічних меж у крапках розриву роду (Функція задовольняючим цим умовам називається монотонною-монотонній-кусочно- монотонної).
ТЕОРЕМА 2. Якщо f(x) періодична функція з періодом , що на відрізку * + разом зі своєї похідної безперервна або має кінцеве число крапок розриву першого роду, то ряд Фур'є функції f(x) у крапках розриву до середнього арифметичного однобічних меж (Функція задовольняючій цій теоремі називається гладкою-гладкій-гладкої-кусочно-гладкої).

#38
Збіжний інтеграл з рядом Фур’ є: f (x) (A( )cos x B( )sin x)d (2.7)
(2.7)
0
Перетворимо за допомогою формули Ейлера підінтегральну функцію у формулі (2.7) до наступного вигляду
|
|
|
|
|
|
|
|
|
|
|
|
|
e j x |
|
e |
|
j x |
|
e j x |
e j x |
|
|
|||
A( )cos x |
B( |
)sin |
x |
A( |
) |
|
|
|
|
|
|
|
|
B( |
) |
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A( ) |
jB( |
) |
e |
j x |
A( |
) |
jB( ) |
e |
j |
x |
c( )e |
j x |
c( |
)e |
j x (2.11) |
|||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де позначено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c( ) |
|
A( ) |
jB( ) |
; c( |
) |
|
|
A( ) |
|
|
jB( ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Тоді
(A( )cos |
x B( |
)sin |
x)d |
|
|
|
(c( )e j x |
c( |
)e j x )d |
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
(2.12) |
|
||
|
c( )e j x d |
c( )e j x d |
|
|
|
c( )e j x d |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для c( |
) |
дістаємо вираз |
|
|
|
|
|
|
|
|
|||||||||||
c( |
) |
|
|
|
A( |
) |
jB( ) |
|
1 |
( |
1 |
|
f (t) cos |
tdt |
j |
1 |
|
f (t) sin tdt) |
|
||
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.13) |
|
|
|
|
|
f (t)(cos t |
j sin |
|
t)dt |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c( |
) |
|
|
1 |
|
f (t)e |
j t dt |
( |
|
0) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(2.14) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Безпосередньо бачимо, що ці формули не втрачають сенс і при |
0 , бо |
||||||||||||||||||||
|
|
|
|
|
|
|
. Тому із формули (2.7) випливає |
|
|
||||||||||||
c( |
) |
|
|
|
c( |
) |
|
|
|||||||||||||

f (x) |
lim |
(A( |
)cos x B( )sin x)d |
lim c( )e j x d (2.15) |
|
|
0 |
|
|
Отже, в точках неперервності функції |
||||
f (x) |
c( |
)e j |
x d (2.16) де |
|
c |
|
( ) |
1 |
f (t)e |
j kt dt. |
k |
|
||||
|
2 |
(2.17) |
|
Вираз для f (x) у формі (2.15) називають комплексною формою інтеграла Фур’є для функції f (x) .
Зауваження. Множник |
1 |
можна записати у будь - яку з формул (2.16) чи (2.17): |
|
2 |
|||
|
|
у вираз для c( ) , як у формулі (2.17), або у формулі (2.16), як це у подальшому буде зроблено для формул перетворення Фур’ є відповідно до стандартів електротехніки.
