
s2_matan_kol_shpore_html_pdf
.pdf
#4
Невласні інтеграли
|
|
f |
|
|
|
I |
|
|
Нехай |
a, |
R і |
x |
a f |
R a, x . Тоді визначено функцію a, |
R , де |
|
|
|
x |
|
|
|
|
|
|
|
I x |
|
f t dt |
|
|
|
|
|
|
|
a |
|
|
|
|
(1) |
|
|
Якщо |
існує |
lim I x |
I |
R , |
то f називається інтегрованою за Ріманом на проміжку a, |
(в |
||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
невласному розумінні), а число I |
її невласним інтегралом першого ряду. При цьому позначають |
|
||||||
I |
f |
x dx |
|
|
|
|
|
|
|
a |
|
|
|
|
(2) |
|
|
Якщо вказана границя не існує, або дорівнює нескінченності, то кажуть, що відповідний невласний не існує, чи розбігається.
Теорема 2. |
(Ознака порівняння) |
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
|
f2 |
|
|
|
|
|
|
Нехай |
функції a, |
R , |
a, |
R невід’ємні, неперервні на області |
|
||||
|
визначення за винятком множин лебегової міри нуль. Якщо |
x0 |
a |
c : x x0 |
|
|||||
|
виконується нерівність |
f1 (x) |
cf 2 (x) , то із |
збіжності I 2 (x) |
слідує збіжність |
|
||||
|
I1 (x) , і з розбіжності I1 (x) слідує розбіжність I 2 (x) . |
|
|
|
|
|||||
|
|
|
|
x |
|
x |
|
|
|
|
Доведення. x |
x0 маємо: I1 (x) |
I1 (x0 ) |
f1 (t)dt |
f 2 (t)dt |
I 2 (x) |
I 2 (x0 ) |
слідує все |
|||
|
|
|
|
x0 |
|
x0 |
|
|
|
|
що треба.
Теорема доведена.
Наслідок 1. |
(Інтегральна ознака збіжності числового ряду) |
|
|
|
|
|
f |
|
|
|
Нехай невід’ємна функція a, |
R неперервна в кожній точці області визначення |
||
|
за виключенням множини лебегової міри нуль, то інтеграл |
f (t)dt збігається тоді і |
||
|
|
|
|
a |
|
|
xn |
1 |
|
|
тільки тоді, коли (xn ) : xn |
для якої ряд |
f t |
dt - збіжний. |
xn
Доведення. З теореми 1 із збіжності інтегралу слідує збіжність ряду для будь-якої послідовності ( xn ) , таким чином необхідність доведена. Для доведення достатності використаємо умову невід’ємності функції f . x R
x |
xn |
|
1 |
|
f (t)dt |
|
f (t)dt , а тому I (x) - монотонна й обмежена, з чого і слідує, що f (t)dt - збіжний. |
a |
n 1 x |
n |
a |
|
|
|
Теорема доведена.

#5
Невласні інтеграли від степеневої функції. Проінтегруємо степеневу функцію по відрізку *a,b+, де 0<a<b. У результаті отримаємо
Виходячи з формули , неважко зробити висновки про збіжність чи розбіжність невласних інтегралів першого й другого родів від степеневої функції прирізних значення параметра p
При p<1 розбігається при p=1
при p>1 збігається

#6
1. Невласні інтеграли
|
|
|
|
f |
|
|
|
|
|
|
I |
Нехай |
a, |
|
R і |
x |
a |
f |
R a, x . Тоді визначено функцію a, |
R , де |
|||
|
|
x |
|
|
|
|
|
|
|
|
|
I x |
f |
t dt |
|
|
|
|
|
|
|
||
|
|
a |
|
|
|
|
|
(1) |
|
||
|
|
|
|
|
|
|
|
|
|||
Якщо |
існує lim I |
x |
I |
R , |
то f називається інтегрованою |
за Ріманом на |
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
проміжку a, |
|
(в невласному розумінні), а число I її невласним інтегралом першого |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ряду. При цьому позначають |
|
|
|
|
|
|
|||||
I |
f x dx |
|
|
|
|
|
|
|
|||
|
a |
|
|
|
|
|
|
(2) |
|
||
|
|
|
|
|
|
|
|
|
|||
Якщо вказана границя не існує, або дорівнює нескінченності, то кажуть, що відповідний невласний не існує, чи розбігається.
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
f |
|
|
|
Повністю |
аналогічно, |
|
для |
функції |
( |
, a] |
R ( |
, ) R |
, |
якщо |
||||||
x |
a |
x, y : x |
y f |
R x, a |
f |
R x, y |
і існує |
|
|
|
|
|
|
|
|||
|
a |
|
|
|
y |
|
|
def |
a |
|
def |
|
|
|
|
|
|
lim |
f |
t dt |
I |
lim |
f |
t dt |
I |
, то I |
f |
t dt |
I |
f t dt . |
|
|
|
||
x |
x |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1. |
(Критерій Коші) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Інтеграл F ( |
) збігається рівномірно на інтервалі I 2 тоді і тільки тоді, |
|
||||||||||||
|
|
|
коли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
A0 |
a : |
A1 |
A0 , A2 |
A0 |
sup |
f (t, |
)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
A1 |
|
|
(6) |
|
|
|
Доведення. Необхідність. Нехай F ( ) рівномірно збігається, тобто для нього |
||||||||||||||||
виконується умова (4), з неї слідує, що |
0 |
A( |
) a : A1 |
A, A2 |
A |
|
|
||||||||||
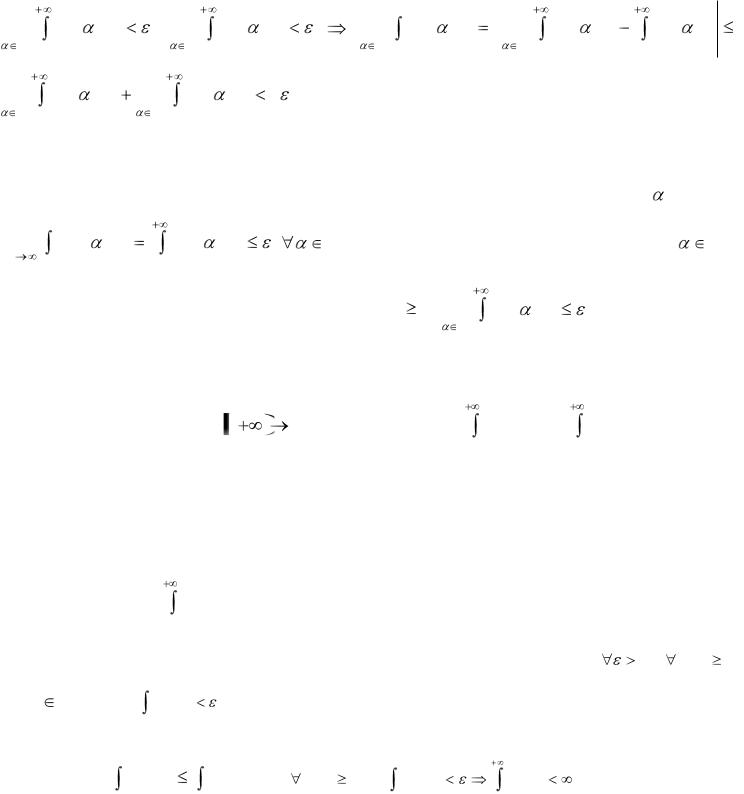
|
|
|
|
|
|
A2 |
|
|
|
sup |
|
f (t, )dt |
, sup |
f (t, )dt |
sup |
f (t, )dt |
sup |
f (t, )dt |
f (t, )dt |
I 2 |
A |
|
I2 |
A |
I2 |
A |
I2 |
A |
A |
|
1 |
|
|
2 |
|
1 |
|
1 |
2 |
sup |
|
f (t, |
)dt |
|
sup |
|
f (t, |
)dt |
2 . |
|
|
|
|
|
|
|
||
I2 |
A |
|
|
|
I2 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Необхідність доведена. |
|
|
|
|
|
|
|
|
||||||||
|
|
Достатність. |
Якщо виконується умова (6), |
з урахуванням збіжності F ( ) |
маємо: |
|||||||||||||
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f (x, |
)dx |
|
|
f (x, |
)dx |
|
I 2 . Тепер переходимо до супремуму по |
I 2 і |
||||||||
A2 |
|
A1 |
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
маємо потрібне, враховуючи що A1 - довільне і A1 |
A sup |
|
f (t, )dt |
|
. |
|
||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
A |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Теорема доведена. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
Теорема Якщо для функції |
a, |
R збігається інтеграл |
|
f (t) |
dt , то |
f (t)dt називається |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|||
абсолютно збіжним. Не абсолютно збіжний інтеграл називається умовно збіжним.
Теорема 3. (Зв’язок абсолютної та умовної збіжності інтегралу)
Якщо f (t)dt абсолютно збігається, то він збіжний.
a
|
|
Доведення. |
Використаємо |
критерій |
Коші. |
Все |
слідує з умови |
0 |
x1, x2 x |
|||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f , |
f |
R[x1 , x2 ] |
|
f (t)dt |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
x2 |
|
|
x2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
та нерівності |
f (t)dt |
|
|
f (t) |
dt . |
x1, x2 |
x |
|
f (t)dt |
f (t)dt |
|
|
||||
|
|
|
x |
|
|
x |
|
|
x1 |
|
a |
|
|
|||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
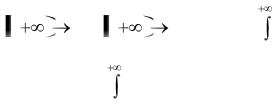
#7.Ознака Абеля збіжності невласного інтегралу 1-го роду: означення: збіжність у підінтегральної функції довільного знаку.
|
f |
g |
Нехай функції a, |
R , a, |
R такі, що f (t)dt - збігається, а функція g - |
|
|
a |
монотонна й обмежена, то |
f (t)g(t)dt - збігається. |
|
|
a |
|
Функцію довільного знаку можно представити у вигляді різниці двох невідємних функцій:
Ф(х) = ф+ (х) - ф- (х)

#8.Ознака Діріхле збіжності невласного інтегралу 1-го роду: означення: збіжність у підінтегральної функції довільного знаку.
|
f |
g |
A |
Нехай функції a, |
R , a, |
R такі, що |
f (t)dt - обмежений, а функція g - |
|
|
|
a |
монотонно прямує до нуля, то |
f (t)g(t)dt - збігається. |
||
|
|
a |
|
Функцію довільного знаку можно представити у вигляді різниці двох невідємних функцій:
Ф(х) = ф+ (х) - ф- (х)

#9.Невласні інтеграли 2-го роду: означення, збіжність,. застосування основної теореми інтегрального числення.
|
f |
|
|
Нехай a, b |
R , і b особлива точка функції f . Нехай f |
необмежена на |
a, b , але |
обмежена |
x a, b на a, x і f R a, x . Позначимо I x I R , то f |
називається |
|
інтегрованою за Ріманом на проміжку a, b , а число I |
її невласним інтегралом другого |
||
b
роду. Тоді невласний інтеграл позначають f x dx і називають збіжним.
a
Якщо у функції ф(х) існує первісна Ф(х), то
І = ∫ab ф(х) dх = Ф(b) – Ф(a). – основна формула інтегрального числе

#10.Невласні інтеграли 2-го роду: основні властивості (теореми 1, 2).
Теорема 1 (Критерій коші)
b
f x dx існує |
0 |
0: x1 , x2 a, b : 0 b x1 |
, 0 b x2 |
виконується |
a
x2
нерівність
x1
f x dx  .
.
Теорема 2 (практична ознака збіжності)
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
Нехай |
a, b |
|
R , x |
a, b |
f |
R a, x . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
Якщо |
c1 |
0 |
1: |
|
lim |
|
b |
x |
|
f |
x |
|
c1, то |
f x dx -збіжний. |
|
|
|
|
x |
b |
0 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
Якщо |
c2 |
0 |
1: |
|
lim |
|
b |
x |
|
f |
x |
|
c2 f |
x dx не існує. |
|
|
|
|
|||||||||||
|
|
|
|
x b |
0 |
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


