Анісімов - Коливання та хвилі

знехтувати добутками n1 n2 (процедура лінеаризації рівнянь). Враховуючи (1.1.5), остаточно дістанемо:

З (1.1.8) легко отримати для n1 чи для n2 рівняння вигляду (1.1.3), де

В більшості реальних ситуацій у взаємодії беруть участь по кілька популяцій хижаків та здобичі, тому коливання чисельності популяцій розмиваються. Однак відомі приклади, коли при спостереженні взаємодії одиночних популяцій хижак - здобич справді спостерігалися протифазні періодичні коливання їхньої чисельності, описувані системою (1.1.8).

Рис.1.1.2. Залежність сили тертя від швидкості: а - сухе тертя, б - в’язке тертя.

Рис.1.1.3. Пружинний маятник із демпфером

в) Пружинний маятник з демпфером.

Сила тертя для випадку сухого тертя нелінійно залежить від швидкості (рис.1.1.2а), тому аналізувати таку систему досить складно. Введемо спеціальний елемент із в’язким тертям -демпфер (рис.1.1.3), для якого у випадку малих швидкостей залежність сили тертя від швидкості можна вважати лінійною (рис.1.1.2б). Тоді, враховуючи закон Гука, рівняння руху для пружинного маятника з демпфером за другим законом Ньютона можна подати у вигляді

mx&& = −kx − hx&,

або

Це - рівняння лінійного дисипативного осцилятора. Воно ж описує, наприклад, коливання струму в контурі, складеному з індуктивності, ємності та опору.

1.1.2. Рівняння консервативного осцилятора.

Повернемося до точного рівняння для математичного маятника (1.1.2). Перепишемо його другий доданок - нелінійну силу, що повертає систему до положення рівноваги - у вигляді

ω02 sin x = ω~02 (x)x = f (x)

(формально можна вважати, що частота коливань тепер є функцією координати). Отже, узагальненням (1.1.2) на випадок довільної нелінійної сили є рівняння

Покажемо, що воно відповідає консервативній системі. Для цього домножимо (1.1.11) на швидкість і проінтегруємо за часом. Дістанемо:

(ми скористалися формулою для похідної від складної функції,

Φ=Φ(x(t))).

В рівнянні (1.1.12) для маятника перший доданок відповідає кінетичній енергії, другий - потенціальній (потенціал (1.1.13) - це робота проти нелінійної сили, що витрачається на виведення системи із стану рівноваги)1. Тоді константа в правій частині (1.1.12) відповідає, очевидно, повній енергії системи, а саме це співвідношення виражає закон збереження енергії.

Взагалі, якщо рівняння руху деякої системи містить лише похідні парних порядків, відповідна система є консервативною, бо зміна знаку часу (заміна t на -t) не впливає на її поведінку. Навпаки, якщо в рівнянні руху присутні похідні непарних порядків, то система не є консервативною (вона може бути дисипативною або/та відкритою, див. рівняння (1.1.10)).

1.1.3. Розв’язок рівняння лінійного дисипативного осцилятора.

Рівняння лінійного дисипативного осцилятора (1.1.10) легко переписати у вигляді системи двох диференціальних рівнянь першого порядку (у фазових змінних):

1 У випадку коливного контуру з варікапом перший доданок відповідає енергії магнітного поля в котушці індуктивності, другий - енергії електричного поля в конденсаторі.

бачимо, що рівняння (1.1.10) описує систему з одним ступенем віль-

ності (п=2, п/2=1).

Загальний розв’язок рівняння (1.1.10) добре відомий:

Довільні константи А,В (або А′, В′) визначаються з початкових умов.

Залежності (1.1.16) для цього випадку подані на рис.1.1.4.

Рис.1.1.4. Вільні коливання лінійного дисипативного осцилятора для випадків ω0>δ (а) та ω0<δ (б).

1.1.4. Метод фазової площини.

У багатьох випадках для аналізу руху систем з одним ступенем вільності зручно користуватися методом фазової площини.

Фазова площина - це площина, на якій по осі абсцис відкладається координата, а по осі ординат - швидкість частинки. Тоді в кожний момент часу стан системи відповідає деякій точці на фазовій площині, яку називають зображувальною точкою. Лінія, яку описує на фазовій площині зображувальна точка, називається фазовою траєкторією. Сукупність усіх можливих фазових траєкторій називається

фазовим портретом системи.

Проаналізуємо, користуючись методом фазової площини, найпростіше рівняння лінійного консервативного осцилятора (1.1.3):

можна переписати рівняння (1.1.3) у фазових змінних х, у, виключивши з нього час:

Видно, що перехід до фазових змінних дозволив знизити порядок рівняння на одиницю, але замість лінійного рівняння вийшло нелінійне. Втім, це рівняння легко проінтегрувати, розділивши змінні:

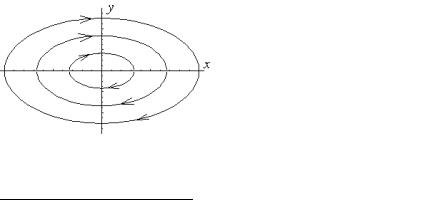
(пор. з (1.1.12)). Фазовий портрет лінійного консервативного осцилятора, як випливає з (1.1.23), являє собою набір вкладених еліпсів

(рис.1.1.5а).

Оскільки додатна швидкість відповідає зростанню координати, у верхній напівплощині фазової площини, де швидкість додатна, зображувальні точки рухатимуться праворуч, відповідно в нижній - ліворуч.

Замінивши в рівнянні руху (1.1.3) ω02 на -ω02, отримаємо випадок перевернутого маятника (для малих відхилень) або візка на гірці з параболічним профілем2. Виконавши ту саму заміну в (1.1.23), отримаємо рівняння, що описує сім’ю гіпербол:

Асимптоти у=±ω0х поділяють усі фазові траєкторії на чотири групи з відмінним характером руху, позначені на рис.1.1.5б римськими цифрами. Наприклад, траєкторії групи І відповідають випадку, коли візок, наїжджаючи на гірку з лівого боку, в деякій точці спиняється і скочується назад. Траєкторії групи ІІ відповідають випадку, коли візок, також наїжджаючи на гірку з лівого боку, перекочується через неї й з’їжджає праворуч, і т.д.

Рис.1.1.5. Фазовий портрет лінійного консервативного осцилятора: а - ω02>0, б - ω02<0.

2 За умови, коли нахил гірки з профілем у(х) є малим, |dy/dx|<<1.

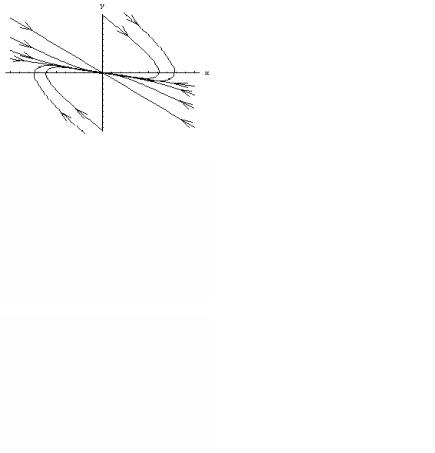
Рис.1.1.6. Ізокліни (штрихами показано напрямок проходження відповідних фазових траєкторій) та фазовий портрет лінійного слабкодисипативного (0<δ<ω0) осци-

лятора.

Видно, що так звана нульова ізокліна (при а=0) на фазовому портреті лінійного слабкодисипативного осцилятора проходить через другий та четвертий квадранти фазової площини, коли δ>0 (дисипація додатна), і через перший та третій квадранти, коли δ<0 (дисипація від’ємна).

При а→∞ маємо у=0. Це справедливо для будь-якої системи: фазові траєкторії завжди (за виключенням окремих особливих випадків) перетинають вісь абсцис під прямим кутом.

Маючи набір ізоклін для різних значень а, можна побудувати фазовий портрет системи. В даному випадку це буде спіраль, що скручується (рис.1.1.6). Їй відповідають коливання з амплітудою, що згасає з часом.

рівняння руху.

Для рівняння лінійного осцилятора (1.1.10) особливою точкою буде, очевидно, точка х=0. Але її характер залежить від співвідношення між параметрами рівняння.

Якщо ω02<0, стаціонарна точка буде нестійкою при будь-яких значеннях параметра дисипації δ. Як уже відзначалося, вона відповідає перевернутому маятнику або візку на гірці. Фазовий портрет для цього випадку поданий на рис.1.1.7а. Видно, що існує пара фазових траєкторій, що починаються в особливій точці, та пара фазових траєкторій, які в ній закінчуються. Стаціонарна точка такого типу діс-

тала назву сідлової точки, або сідла.

Якщо ω02>0, характер особливої точки буде істотно залежати від значення δ.

При δ=0, як уже вказувалося (п.1.1.4), фазовий портрет системи являє собою набір вкладених еліпсів (рис.1.1.7б). Стаціонарна точка в цьому випадку є ізольованою - в ній не починається і не закінчується жодна фазова траєкторія. Маємо справу із особливою точкою типу центр.

При 0<δ<ω0 фазовий портрет системи являє собою спіраль, що скручується (п.1.1.5, рис.1.1.7в). Відповідну стаціонарну точку називають стійким фокусом. При малій від’ємній дисипації (0<-δ<ω0) отримаємо спіраль, що розкручується (рис.1.1.7г), і нестійкий фо-

кус.

Нарешті, у випадку сильної дисипації - при δ>ω0 - реалізується режим аперіодичного згасання коливань (див.п.1.1.3). Фазовий портрет системи являтиме собою набір деформованих парабол (рис.1.1.7д), що закінчуються в особливій точці типу стійкий вузол. При сильній від’ємній дисипації - 0<ω0<-δ - матимемо аперіодичне зростання коливань (рис.1.1.7е). У цьому випадку фазові траєкторії починаються з особливої точки типу нестійкий вузол.

Рис.1.1.7. Особливі точки лінійного осцилятора: а - сідло (ω02<0); б - центр (δ=0, ω02>0); в - стійкий фокус (0<δ<ω0); г - нестійкий

фокус(0<-δ<ω0); д - стійкий вузол (0<ω0<δ); е - нестійкий вузол(0<ω0<-

δ).

Контрольні питання до розділу 1.1.

1.1.1.Запропонуйте кілька прикладів, що ілюструють умовність поняття кількості ступенів вільності.

1.1.2.Під яким кутом фазові траєкторії перетинають вісь абсцис?

1.1.3.Як обирається напрямок руху вздовж фазової траєкторії на фазовій площині?

1.1.4.Поясніть якісно, чому нульова ізокліна для дисипативних осциляторів зсувається в другий та четвертий квадранти.

1.1.5.У чому переваги методу аналізу руху динамічних систем за допомогою фазової площини?

1.1.6.Як впливає наявність дисипації на поведінку системи в околі сідлової точки? Дайте якісне пояснення.

1.1.7.Опишіть послідовні зміни характеру особливої точки лінійно-

го дисипативного осцилятора (ω02>0) при зміні параметра дисипації від -∞ до +∞.

1.1.8.Вкажіть якісну відмінність між різними групами фазових траєкторій для сильнодисипативного лінійного осцилятора (рис.1.1.7д). Чим відрізняються розв’язки рівняння руху для цих випадків?

1.1.9.Яким розв’язкам відповідають сепаратриси (прямі лінії) на фазовому портреті сильнодисипативного лінійного осцилятора

(рис.1.1.7д)?

Задачі до розділу 1.1.

1.1.1. Побудувати фазовий портрет для рівняння лінійного дисипативного осцилятора

користуючись методом ізоклін. Розглянути випадки:

а) 0<δ<ω0; б) 0<-δ<ω0; в) 0<ω0<δ; г)0<ω0<-δ.

Вказівка: перейти до безрозмірного часу: t→ω0t. Для двох останніх випадків записати рівняння для сепаратрис; проаналізувати взаємне розташування сепаратрис, нульової ізокліни та ізоклін, що відповідають нахилу а=±1; визначити, якому нахилу відповідає ізокліна, що збігається з віссю ординат.

1.1.2. Вказати якісну різницю між ізоклінами для фазового портрета лінійного дисипативного осцилятора для випадків:

а) δ<ω0 та δ>ω0;

б) -δ<ω0 та -δ>ω0.

1.1.3. Побудувати фазовий портрет для рівняння:

x&&+ 2δ x& −ω 20 x = 0, ω 20 > 0

(візок на гірці) методом ізоклін. Розглянути випадки:

а) δ>0; б) δ<0.

Вказівка: перейти до безрозмірного часу: t→ω0t. Записати рівняння для сепаратрис.

1.1.4. Побудувати точний фазовий портрет лінійного дисипативного осцилятора

Розглянути випадки:

а) 0<δ<ω0; б) 0<-δ<ω0; в) δ>ω0;

г) -δ>ω0.

Вказівка: для перших двох випадків послідовно скористатися замінами u=ωx, v=y+δx, де ω=(ω02-δ2)1/2, а потім перейти до полярних

координат згідно співвідношень u=ρ cos ϕ, v=ρ sin ϕ. Для двох інших випадків скористатись заміною u=y+q1x, v=y+q2x, де q1,2=δ±(δ2- ω02)1/2. Після побудови фазового портрету в координатах u, v нанести на графік осі х, у і якісно проаналізувати, як деформується фазовий портрет при поверненні до "старих" координат.

1.1.5. Побудувати точний фазовий портрет для рівняння :

Розглянути випадки:

а) δ>0; б) δ<0.

Вказівка: скористатися заміною u=y+q1x, v=y+q2x, де q1,2=δ±(δ2+ω02)1/2. Після побудови фазового портрету в координатах u, v нанести на графік осі х, у і якісно проаналізувати, як деформується фазовий портрет при поверненні до "старих" координат.

1.1.6.Густина рідини при віддаленні від дна посудини зменшується до нуля за лінійним законом. Знайти частоту малих коливань поплавка, що плаває в такій рідині. Розміри поплавка вважати малими порівняно з характерним розміром L, на якому густина рідини помітно змінюється. Тертям знехтувати.

1.1.7.Визначити частоту вертикальних коливань поплавка на воді. Поплавок являє собою прямий циліндр, маса якого зосереджена в нижній частині. За яких амплітуд його коливання можна вважати лінійними?

1.1.8.Визначити частоту малих коливань електрона в одновимірній кристалічній гратці з періодом d. Електричний потенціал розподіле-

ний за законом: ϕ(x)=ϕ0+ϕmcos(2πx/d). За яких амплітуд такі коливання можна вважати лінійними?

1.1.9.Візок маси m без тертя здійснює коливання поблизу дня ями з профілем y=x2/L. Рух відбувається в площині xy.

а) За яких амплітуд (уздовж x) такі коливання можна вважати лінійними? Знайти власну частоту коливань для цього випадку.

б) Визначити період вертикальних коливань візка.

1.1.10.Візок маси m без тертя здійснює коливання поблизу дна ями з профілем y=f(x). Рух відбувається в площині xy. Записати диференціальні рівняння нелінійних коливань візка для координат x та y, якщо мінімум потенціалу відповідає точці (x0, y0).

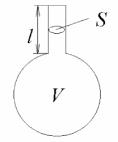
1.1.11. Визначити частоту малих коливань акустичного резонатора, якщо газ, що його заповнює, задовольняє рівнянню адіабати

PVγ=const. Скористатись позначенням для швидкості звуку cs=(γP0/ρ0)1/2, де P0 і ρ0 - рівноважні тиск і густина газу. За яких амплітуд такі коливання можна вважати лінійними?

Вказівка: скористатись аналогією з пружинним маятником, вважаючи, що роль маси відіграє газ у горловині, а роль пружини – газ у колбі.

1.1.12. Знайти частоту малих коливань частинки маси М поблизу мінімуму потенціалу:

(різновиди потенціалу міжмолекулярної взаємодії);

д) Φ (x) = −A exp[− α(x − b)2 ];

е) Φ (x) = −Ax exp[− α x]; є) Φ (x) = −Ax 2 exp[− αx].

За яких амплітуд такі коливання можна вважати лінійними?

1.1.13. Визначити рівноважну чисельність популяцій та частоту малих коливань в системі хижак - здобич. Чисельність хижаків N1 та здобичі N2 задовольняє модифікованим рівнянням Вольтерра (з урахуванням обмеженості харчових ресурсів):

N&1 = −ε1 N1 +γ1 N1 N2 ; N&2 = ε2 N2 − (ε2 K)N22 −γ 2 N1 N2 .

За яких амплітуд такі коливання можна вважати лінійними? Чи можна вважати цю систему консервативною (для довільних відхилень від рівноважної чисельності)?

1.1.14. Взаємні перетворення проміжних продуктів хімічної реакції Лотки, що мають концентрації X та Y, описуються системою кінетичних рівнянь:

Знайти рівноважні значення концентрацій X0, Y0 та частоту малих коливань навколо цих концентрацій. За яких амплітуд такі коливання можна вважати лінійними? Чи можна вважати цю систему консервативною (для довільних відхилень від рівноважних концентрацій)?

1.1.15. Визначити частоту вільних поздовжніх коливань електронів у холодній плазмі з важкими іонами. Поведінка системи описується рівняннями

∂∂nt + div(nvr) = 0; m dvdt = −eEr; divEr = −4π e(n − n0 ),

де n та n0=const - концентрації електронів та іонів, v - швидкість спрямованого руху електронів, E - напруженість електричного поля. 1.1.16. Побудувати розв’язок рівняння

користуючись методом повільних амплітуд3. Розглянути випадки:

а) ω0>>δ>0;

б) ω0>>-δ>0.

Порівняти отримані результати з відомим точним розв’язком.

1.1.17. Рівняння, що описують коливання поляризації і різниці населеностей у дворівневій системі (найпростіша модель лазера) після увімкнення накачування, мають вигляд:

де p - поляризація, N - різниця населеностей, N0 - її рівноважне значення (за відсутності накачування), E=Emcos ω0t - напруженість поля накачування, ω0 - частота квантового переходу, µ12 – матричний елемент, що характеризує ймовірність цього переходу, T1,2 - часи поздовжньої та поперечної релаксації (ω0T1,2<<1).

Вважаючи, що поляризація має характер коливань на частоті ω0 з повільною амплітудою, отримати для неї вкорочене рівняння. Знайти рівноважні значення амплітуди поляризації та різниці населеностей за наявності накачування, частоту та час згасання їхніх коливань. Намалювати графік часової залежності різниці населеностей, якщо накачування увімкнено в момент часу t=0, коли система знаходилася в рівноважному стані.

Вказівка. Доданком із подвійною частотою в правій частині рівняння для різниці населеностей знехтувати. Записати систему рівнянь для відхилень поляризації та різниці населеностей від рівноважних значень. Вважати виконаною умови

µ12 EmT1,2 <<1.

h

1.1.18. Візок маси т без тертя здійснює коливання в ямі з профілем у(х). Знайти функцію у(х), яка забезпечує гармонічність коливань у напрямку х.

1.2. Вимушені коливання лінійного осцилятора під дією гармонічної сили.

В багатьох випадках осцилятори взаємодіють між собою. Якщо зворотним впливом другого осцилятора на перший можна знехтувати, то прямий вплив першого на другий зручно подати в формі заданої зовнішньої сили. Коливання, що здійснюються під впливом зовнішньої сили, називаються вимушеними.

1.2.1. Приклади вимушених коливань лінійних осциляторів.

y = −2δy −ω0 x + f (τ),

що має вигляд (В.1) (додаткову змінну τ = t введено для того, щоб праві частини формально не залежали від часу). Бачимо, що наявність зовнішньої сили еквівалентна додаванню половини ступеню вільності. Отже, осцилятор, на який діє зовнішня сила, являє собою систему з півтора ступенями вільності.

Прикладами вимушених коливань лінійних осциляторів можуть бути коливання маятника під дією зовнішньої сили або коливання в контурі під дією зовнішньої змінної напруги (рис.1.2.1а,б). В усіх випадках наявність зовнішньої сили f(t) призводить до того, що рівняння руху (1.1.9) (або (1.1.2) для випадку консервативного осцилятора) стає неоднорідним:

Рис.1.2.1. Приклади лінійних осциляторів, на які діють зовнішні сили: а - пружинний маятник, б - коливний контур.

1.2.2. Осцилятор під дією зовнішньої сили - система з півтора ступенями вільності.

Перепишемо рівняння (1.2.1) у вигляді системи:

1.2.3. Коливання лінійного консервативного осцилятора під дією гармонічної сили.

Проаналізуємо спочатку коливання консервативного осцилятора під дією зовнішньої гармонічної сили, що описуються рівнянням

Як відомо з теорії диференціальних рівнянь, загальний розв’язок лінійного неоднорідного рівняння може бути записаний як сума загального розв’язку відповідного однорідного рівняння та частинного розв’язку неоднорідного рівняння. Називатимемо ці частини вільною і вимушеною складовою коливань:

Константи А і В, як і для чисто вільних коливань, знаходяться з початкових умов.

Зокрема, для нульових початкових умов ( x(t = 0) = 0, x&(t = 0) = 0 ) отримаємо:

(1.2.5) (рис.1.2.2а). Рух системи являє собою биття двох коливань з однаковими амплітудами - вільних з частотою ω0 та вимушених з часто-

тою p. Оскільки згасання відсутнє, биття триватимуть як завгодно довго. Період биттів визначається співвідношенням

Для інших початкових умов амплітуди вільних та вимушених коливань вже не будуть рівними, але в загальному випадку вони будуть ненульовими, тому биття збережуться.

Розглянемо тепер випадок резонансу, коли ω0=p. В цьому випадку замість (1.2.5) дістанемо:

(рис.1.2.2б). Видно, що в цьому випадку має місце необмежене лінійне за часом (секулярне) зростання амплітуди коливань.

Зрозуміло, що в реальних системах секулярне зростання коливань не спостерігається. Воно обмежується за рахунок наявності дисипації або нелінійності.

1.2.4. Вплив дисипації на коливання лінійного осцилятора під дією гармонічної сили.

Для лінійного осцилятора з дисипацією замість (1.2.1) одержимо:

Рис.1.2.2. Коливання лінійного консервативного осцилятора під дією гармонічної зовнішньої сили для нульових початкових умов: а - ω0≠p, б - ω0=p.

Розв’язок цього рівняння для нульових початкових умов та слабкої дисипації (δ<<ω0) має вигляд:

(рис.1.2.3а,б).

Видно, що у нерезонансному випадку згасання вільної складової призводить до зникнення биття за час порядку 1/δ, після чого в системі залишаються лише чисто вимушені коливання. Відзначимо, що викид амплітуди в момент часу t≈π/ ω0-p приблизно вдвічі перевищує значення, що встановлюється при t→∞. Цю обставину слід мати на увазі при розрахунках запасу міцності систем, в яких збу-