
Module1_theory_zadachi
.doc-
Сума геометричних векторів (означення). Довести, що операція додавання векторів комутативна і асоціативна, тобто

 для довільних векторів
для довільних векторів
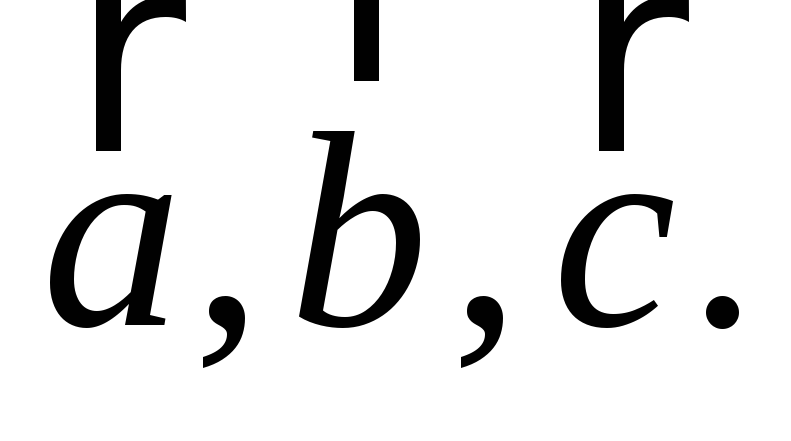
-
Добуток геометричного вектора на число (означення). Довести, що для довільних дійсних чисел , для довільного вектора
 виконується
виконується
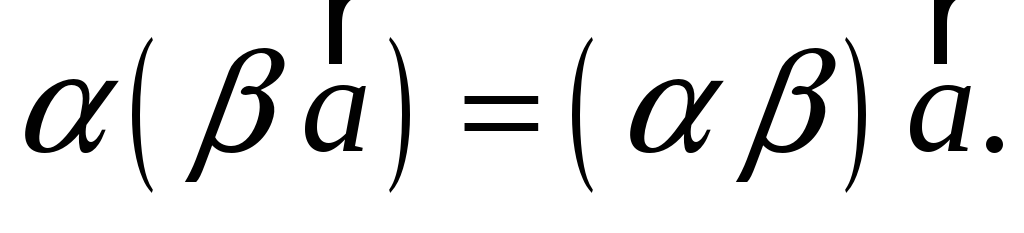
-
Означення рівності двох геометричних векторів. Довести, що для довільного дійсного числа , для довільних векторів
 виконується
виконується

-
Добуток геометричного вектора на число (означення). Довести, що для довільних дійсних чисел , для довільного вектора
 виконується
виконується

-
Означення векторного простору. Навести приклад векторного простору (з доведенням).
-
Означення лінійно незалежної, лінійно залежної системи векторів. Довести, що два неколінеарних вектори на площині, три некомпланарних вектори в просторі є лінійно незалежними.
-
Означення лінійно незалежної, лінійно залежної системи векторів. Довести, що два вектори на прямій, три вектори на площині є лінійно залежними.
-
Означення лінійно незалежної, лінійно залежної системи векторів. Необхідна і достатня умова того, що система векторів є лінійно залежною (з доведенням).
-
Базис векторного простору, координати вектора в базисі (означення). Твердження про єдиність розкладу вектора за базисом (з доведенням).
-
Базис векторного простору, координати вектора в базисі (означення). Твердження про координати вектора, який є лінійною комбінацією заданих векторів (з доведенням).
-
Базис векторного простору (означення). Твердження про базис на прямій, на площині (з доведенням).
-
Базис векторного простору (означення). Твердження про базис в просторі (з доведенням).
-
Загальна декартова система координат (означення). Задача про поділ відрізка у заданому відношенні.
-
Ортонормований базис, прямокутна декартова система координат (означення). Задача про поділ відрізка у заданому відношенні.
-
Проекція точки на площину, вектора на площину (означення). Довести, що для довільної площини
 ,
довільних векторів
,
довільних векторів
 виконується
виконується
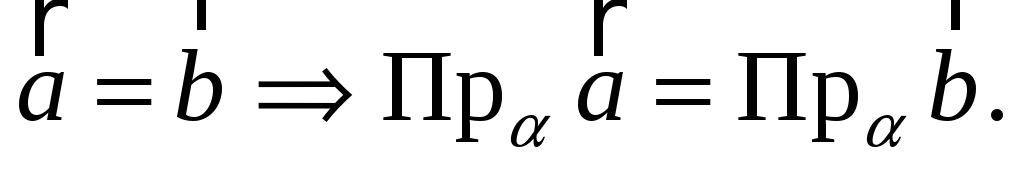
-
Проекція точки на пряму, вектора на пряму в просторі (означення). Довести, що для довільних векторів
 прямої
прямої
 виконується
виконується
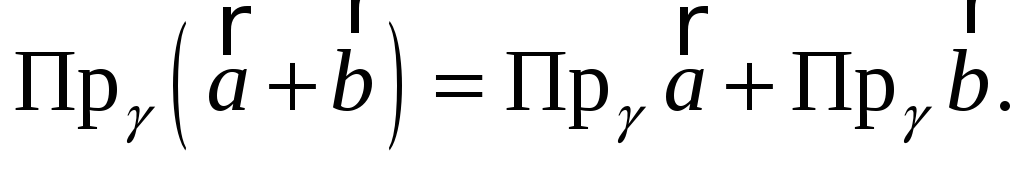
-
Проекція точки на пряму, вектора на площину (означення). Довести, що для довільних вектора
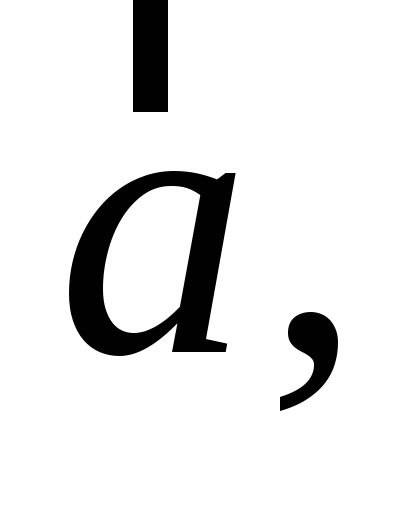 числа
числа
 ,
площини
,
площини
 виконується
виконується
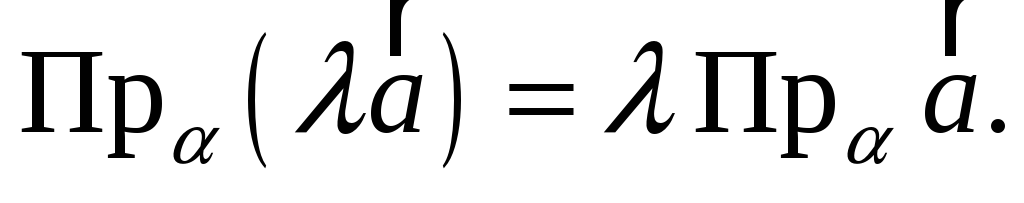
-
Проекція вектора на вектор (означення). Довести, що для довільних векторів
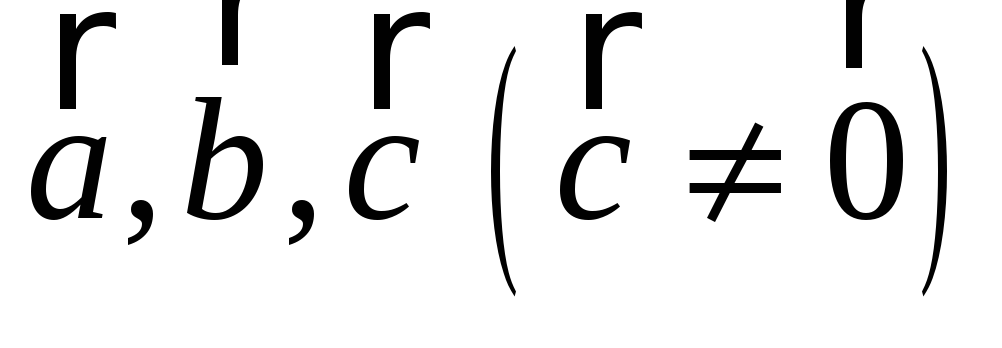 виконується
виконується

-
Проекція вектора на вектор (означення). Довести, що для довільних векторів
 виконується
виконується
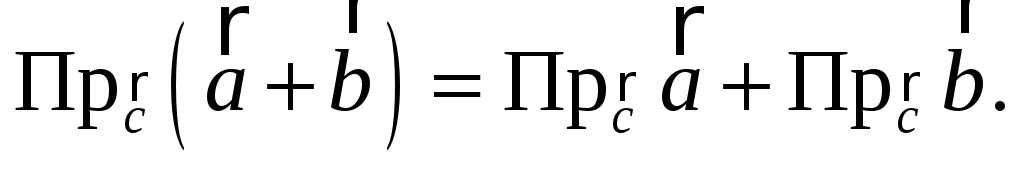
-
Скалярний добуток векторів (означення). Твердження про властивості скалярного добутку (з доведенням).
-
Скалярний добуток векторів (означення). Вираз скалярного добутку через координати векторів в довільному і ортонормованому базисі (з доведенням).
-
Скалярний добуток векторів (означення). Геометричні властивості скалярного добутку.
-
Векторний добуток векторів (означення). Довести, що

-
Векторний добуток векторів (означення). Довести, що для довільного дійсного числа виконується
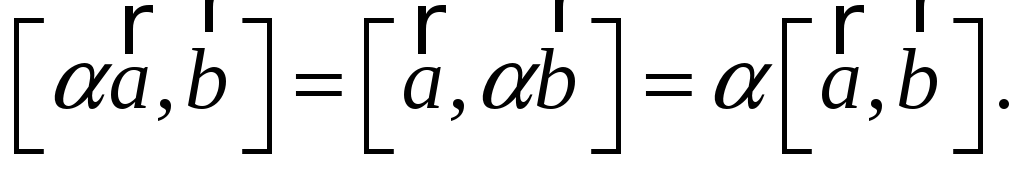
-
Векторний добуток векторів (означення). Довести, що

-
Вираз векторного добутку через координати векторів в довільному і ортонормованому базисі (з доведенням).
-
Мішаний добуток векторів (означення). Довести, що мішаний добуток векторів за модулем дорівнює об’єму паралелепіпеда, який побудований на цих векторах.
-
Мішаний добуток векторів (означення). Довести, що мішаний добуток векторів є додатним (від’ємним), якщо ці вектори є правою (лівою) трійкою.
-
Мішаний добуток векторів (означення). Довести, що мішаний добуток векторів дорівнює 0 тоді і тільки тоді, коли вектори є компланарними.
-
Мішаний добуток векторів (означення). Довести, що
 Довести, що якщо переставити місцями
два вектори в мішаному добутку, то знак
мішаного добутку зміниться на протилежний.
Довести, що мішаний добуток векторів
лінійна функція кожного з аргументів.
Довести, що якщо переставити місцями
два вектори в мішаному добутку, то знак
мішаного добутку зміниться на протилежний.
Довести, що мішаний добуток векторів
лінійна функція кожного з аргументів. -
Вираз мішаного добутку через координати векторів в довільному і ортонормованому базисі (з доведенням).
-
Подвійний векторний добуток (означення). Довести, що

-
Подвійний векторний добуток (означення). Довести, що

-
Алгебраїчна лінія на площині, алгебраїчна поверхня в просторі (означення). Навести приклад алгебраїчної лінії на площині, алгебраїчної поверхні в просторі.
-
Рівняння площини, яка проходить через задану точку, паралельно двом неколінеарним векторам (у виді мішаного добутку і у виді мішаного добутку в координатній формі) (з доведенням).
-
Рівняння площини, яка проходить через задану точку, паралельно двом неколінеарним векторам (векторно-параметричне і параметричне рівняння) (з доведенням).
-
Рівняння площини, яка проходить через три задані точки (у виді мішаного добутку і у виді мішаного добутку в координатній формі) (з доведенням).
-
Рівняння площини, яка проходить через три задані точки (векторно-параметричне і параметричне рівняння) (з доведенням).
-
Довести, що рівняння площини в ДСК є рівнянням першого порядку. Загальне рівняння площини.
-
Довести, що рівняння першого порядку в ДСК є рівнянням площини. Загальне рівняння площини.
-
Рівняння площини, яка проходить через задану точку, перпендикулярно до заданого вектора (з доведенням). Знаходження відстані від точки до площини.
-
Рівняння прямої в просторі (векторно-параметричне, векторне, параметричне, канонічне) (з доведенням).
-
Рівняння прямої в просторі через дві точки (векторно-параметричне, векторне, параметричне, канонічне) (з доведенням).
-
Загальне рівняння прямої в просторі. Зведення загального рівняння прямої в просторі до канонічного.
-
Канонічне рівняння прямої в просторі. Знаходження відстані від точки до прямої в просторі.
-
Канонічне рівняння прямої в просторі. Знаходження відстані між двома мимобіжними прямими просторі.
-
Заміна базису в просторі. Взаємозв’язок між координатами вектора в старому і новому базисі. Випадок ОНБ.
-
Заміна ДСК в просторі. Взаємозв’язок між координатами точки в старій і новій ДСК. Випадок ПДСК.
-
Заміна базису на площині. Взаємозв’язок між координатами вектора в старому і новому базисі. Випадок ОНБ.
-
Заміна ДСК на площині. Взаємозв’язок між координатами точки в старій і новій ДСК. Випадок ПДСК.
Типи задач модульної контрольної № 1
Задача 1
Задано
вектори
![]() Знайти
Знайти
-

-
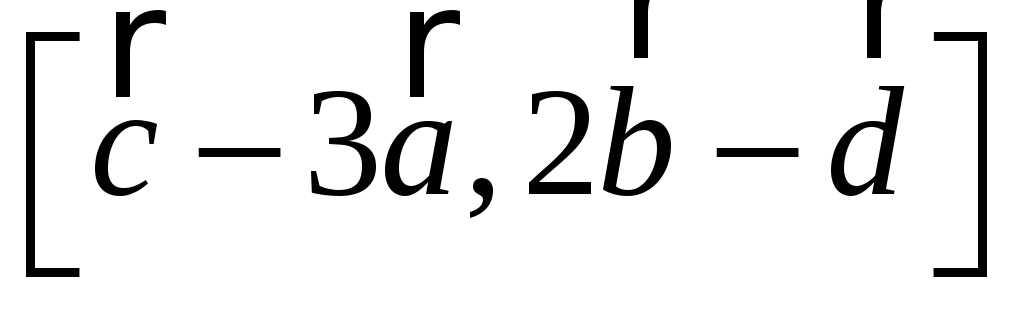
-
перевірити, якою (правою чи лівою) буде трійка векторів
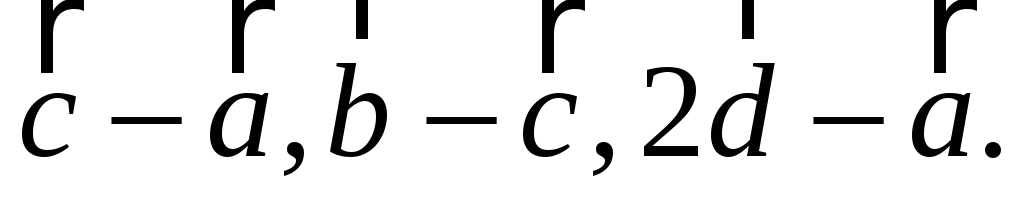
-
об’єм паралелепіпеда, який побудований на векторах
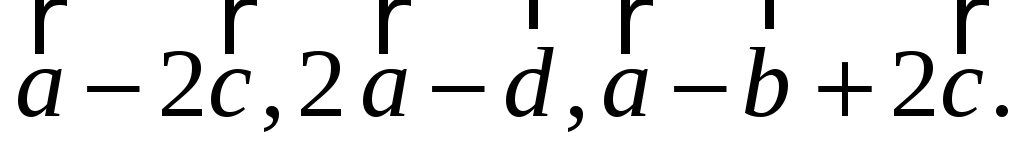
-
перевірити, чи будуть вектори
 компланарними.
компланарними. -
об’єм тетраедра, який побудований на векторах

-

Задача 2
-
Скласти рівняння площини, яка проходить через точку
 паралельно
прямим
паралельно
прямим
 і
і

-
Скласти рівняння площини, яка проходить через точки
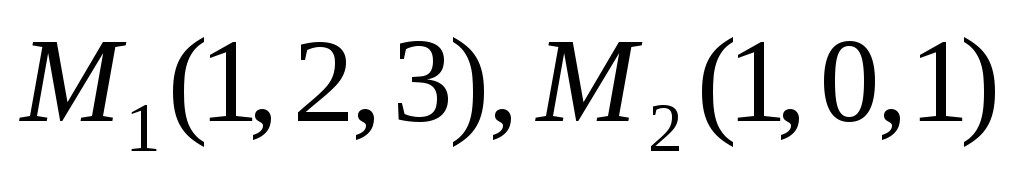 паралельно вектору
паралельно вектору
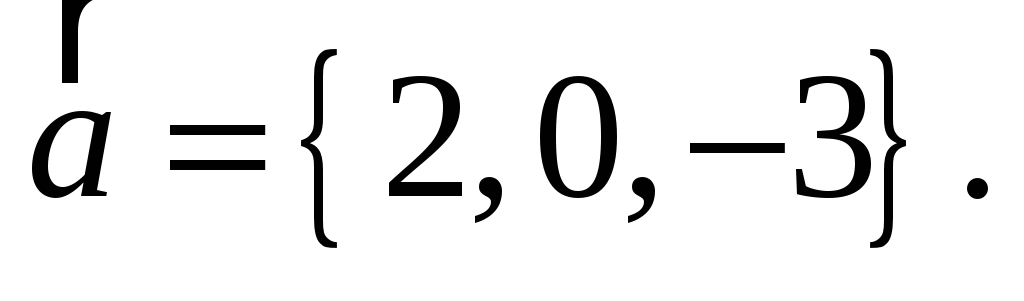
-
Скласти рівняння площини, яка проходить через точки
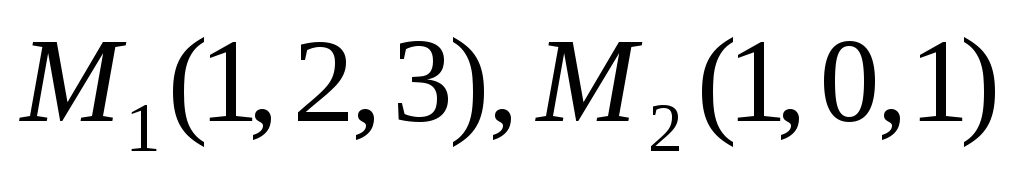 паралельно вісі Ox
(або
Oy,
Oz).
паралельно вісі Ox
(або
Oy,
Oz). -
Скласти рівняння площини, яка проходить через точку
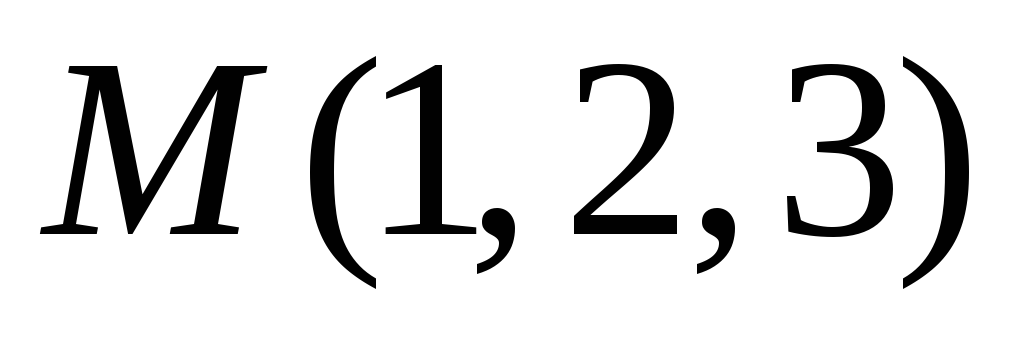 і
пряму
і
пряму

-
Скласти рівняння площини, яка проходить через точки
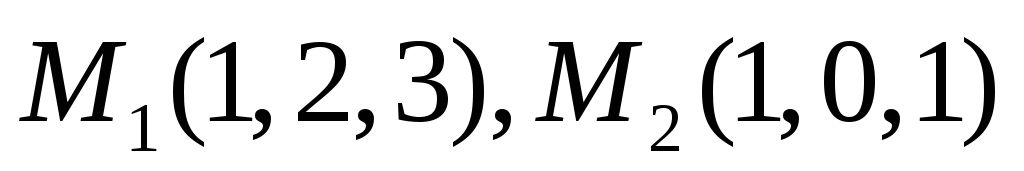 паралельно прямій
паралельно прямій
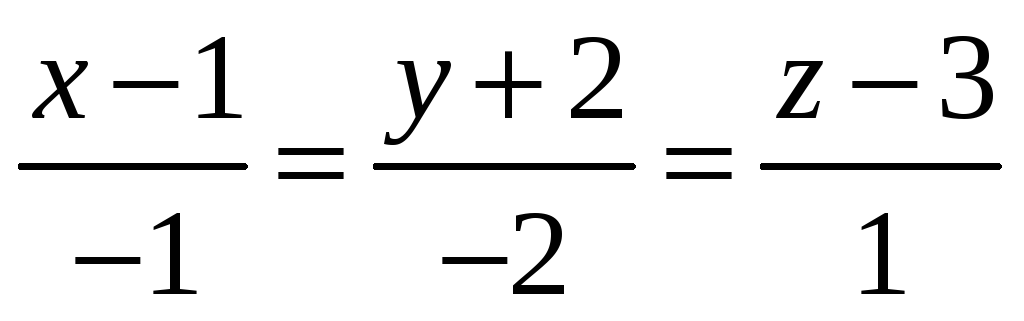
-
Скласти рівняння площини, яка проходить через пряму
 паралельно вектору
паралельно вектору
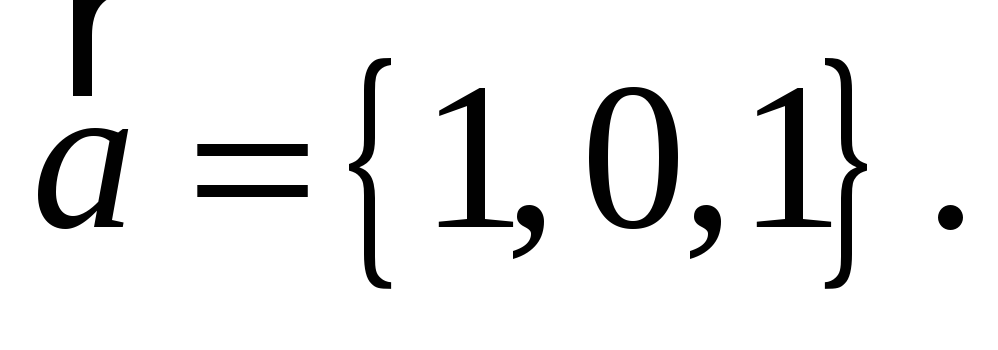
Задача 3
-
Знайти відстань від точки
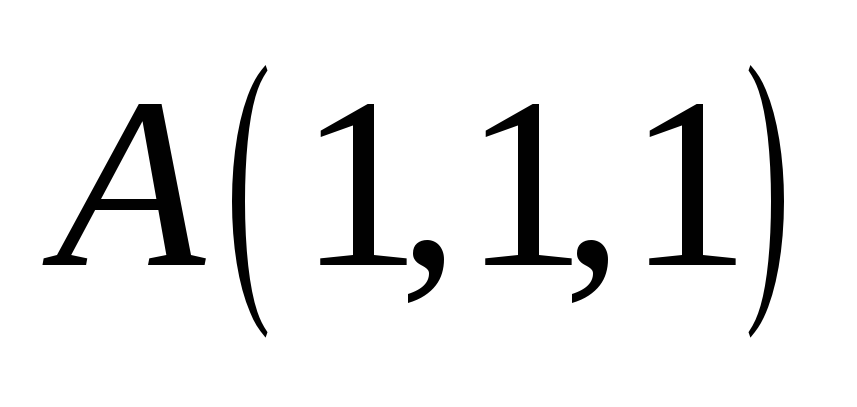 до площини
до площини

-
Нехай
 .
Чи перетинає площина
.
Чи перетинає площина
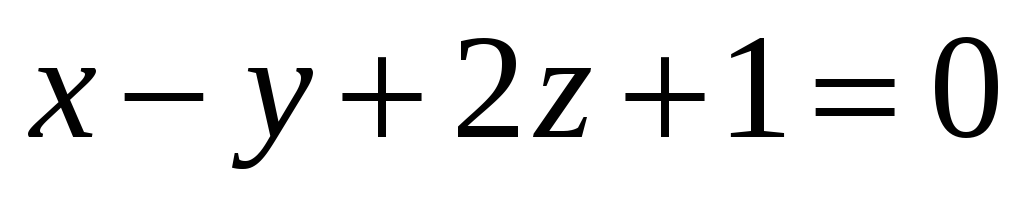 відрізок
відрізок
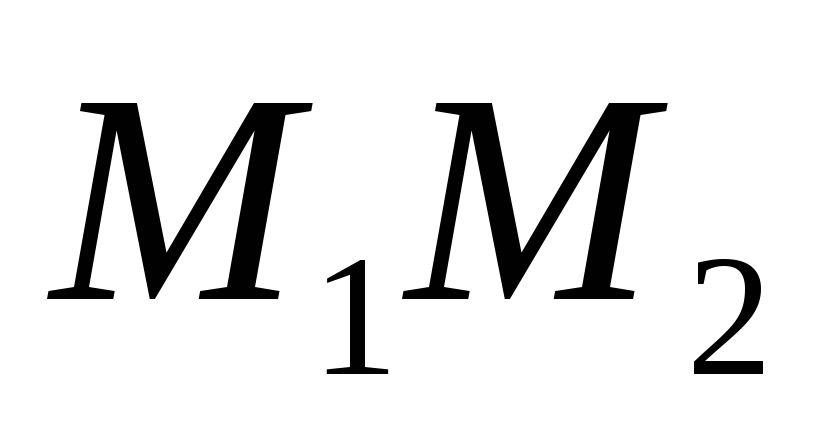 ?
? -
Знайти відстань між паралельними площинами
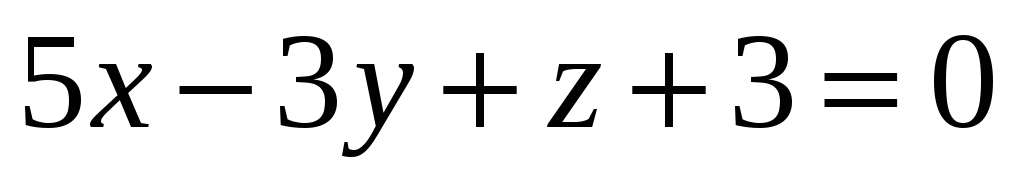 і
і
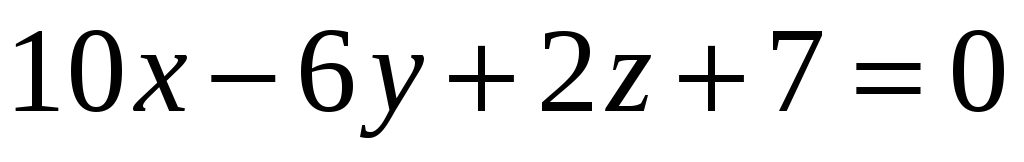 .
.
Задача 4
-
Знайти проекцію точки
 на площину
на площину
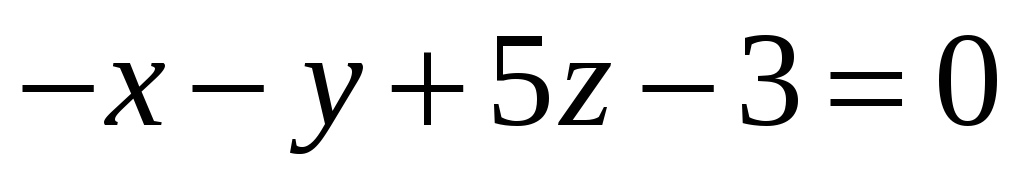 [
[ -
Знайти проекцію точки
 на пряму
на пряму

-
Знайти точку, яка симетрична точці
 відносно прямої
площини
відносно прямої
площини

-
Знайти точку, яка симетрична точці
 відносно прямої
відносно прямої

-
Звести загальне рівняння прямої
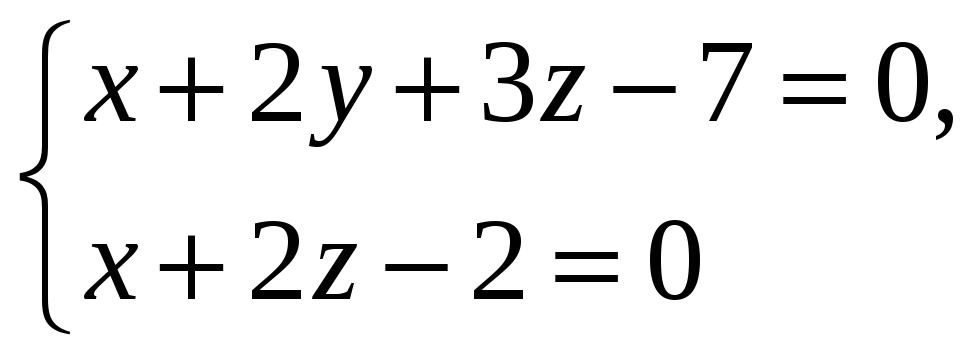 до канонічного.
до канонічного. -
Скласти рівняння прямої, яка проходить через точку
 паралельно прямій
паралельно прямій
 .
.
