zadachi_teorver

Гіпергеометричний розподіл. Дана сукупність об’єктів, серед яких об’єктів є відміченими. Обирається навмання об’єктів. Нехай - випадкова величина, яка дорівнює кількості відмічених об’єктів серед обраних. Ймовірність того, що , задається формулою

, .

Набір таких ймовірностей називається гіпергеометричним розподілом.

Позначення: .

Біноміальний розподіл. Нехай - випадкова величина, яка дорівнює кількості успіхів в серії незалежних випробувань. Якщо ймовірність успіху при одному випробуванні дорівнює (ймовірність невдачі ), ймовірність того, що має вигляд

, .

Такий набір ймовірностей має назву біноміального розподілу.

Позначення: .

Геометричний розподіл. Нехай є серія незалежних випробувань. Результатом кожного окремого випробування може бути або успіх з ймовірністю , або невдача з ймовірністю . Випробування тривають до появи першого успіху. Випадкова величина визначає кількість невдач, які відбулись в серії випробувань. Тоді ймовірність того, що , дорівнює

, .

Цей набір ймовірностей визначає геометричний розподіл.

Позначення: .

Від’ємний біноміальний розподіл. Якщо серія незалежних випробувань триває до появи - го успіху, ймовірність того, що при цьому кількість невдач буде дорівнювати (), задається виразом

, .

Набір відповідних ймовірностей має назву від’ємного біноміального розподілу.

Позначення: .

Розподіл Пуассона. Випадкова величина , яка приймає значення , розподілена за законом Пуассона з параметром , якщо

.

Позначення: .

Показниковий (експоненціальний) розподіл. Випадкова величина має показниковий розподіл, якщо

Позначення: .

Гама-розподіл. Якщо розподіл густини ймовірності випадкової величини має вигляд

кажуть, що випадкова величина розподілена за гама-законом.

Позначення: .

Бета-розподіл. Випадкова величина розподілена за бета-законом, якщо

Позначення: .

Нормальний розподіл (розподіл Гаусса). Випадкова величина розподілена нормально, якщо

.

Позначення: .

Логнормальний розподіл. Випадкова величина розподілена логнормально, якщо

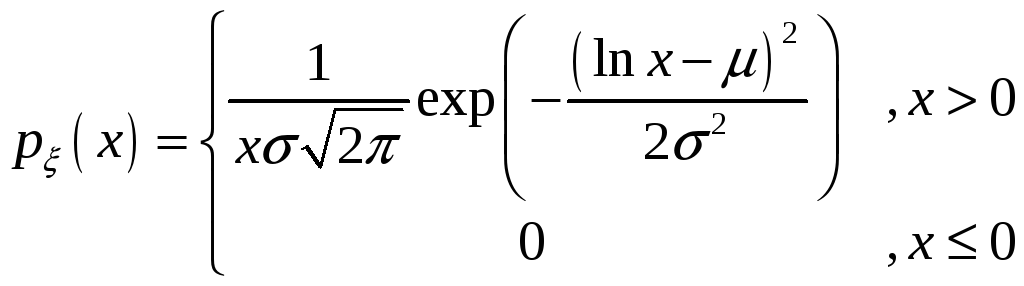
Позначення: .

Розподіл (розподіл Пірсона). Випадкова величина розподілена за законом з ступенями вільності, якщо

Позначення: .

Розподіл Ст’юдента. Випадкова величина розподілена за законом Ст’юдента з ступенями вільності, якщо

.

Позначення: .

ЗАДАЧІ

7.14 Знайти розподіл густини ймовірності випадкової величини , якщо задана густина розподілу ймовірності випадкового вектора .

7.15 Випадкові величини та незалежні та розподілені рівномірно на відрізку . Знайти розподіл густини ймовірності випадкової величини .

7.16 Випадкові величини та незалежні та розподілені за показниковим законом з густиною розподілу ймовірності , . Знайти розподіл густини ймовірності випадкової величини .

7.17 Знайти розподіл густини ймовірності випадкової величини , якщо задана густина розподілу ймовірності випадкового вектора .

7.18 Випадкові величини та незалежні та розподілені рівномірно на відрізку . Знайти розподіл густини ймовірності випадкової величини .

7.19 Випадкові величини та незалежні та розподілені за показниковим законом з густиною розподілу ймовірності , . Знайти розподіл густини ймовірності випадкової величини .

7.20 Знайти розподіл густини ймовірності випадкової величини , якщо задана густина розподілу ймовірності випадкового вектора .

7.21 Випадкові величини та незалежні та розподілені рівномірно на відрізку . Знайти розподіл густини ймовірності випадкової величини .

7.22 Знайти розподіл густини ймовірності випадкової величини , якщо задана густина розподілу ймовірності випадкового вектора .

7.23 Випадкові величини та незалежні та розподілені рівномірно на відрізку . Знайти розподіл густини ймовірності випадкової величини .

7.24 Випадкові величини та незалежні та розподілені за показниковим законом з густиною розподілу ймовірності , . Знайти розподіл густини ймовірності випадкової величини .

7.25 Випадкові величини та незалежні та розподілені за законом та відповідно. Знайти розподіл випадкової величини .

7.26 Випадкові величини та незалежні та розподілені за законом . Знайти розподіл густини ймовірності випадкової величини .

7.27 Випадкові величини та незалежні, причому розподілена за законом , а величина . Знайти розподіл густини ймовірності випадкової величини .

7.28 Випадкові величини та незалежні та розподілені за законом та відповідно. Знайти розподіл випадкових величин та .

7.29 Випадковий вектор має розподіл густини ймовірності

, , .

Знайти , . Чи є незалежними випадкові величини та ?

7.30 Випадковий вектор має розподіл густини ймовірності

, , .

Визначити сталу . Чи є незалежними випадкові величини та ?

7.31 Випадкова точка рівномірно розподілена в області . Чи будуть незалежними полярні координати цієї точки? Чи будуть незалежними декартові координати ?

7.32 Випадкові величини та незалежні та мають показниковий розподіл з параметром (). Довести, що випадкові величини та є незалежними.

7.33 Випадкові величини та незалежні та розподілені за законом . Довести, що випадкові величини та також є незалежними.

7.34 Випадкові величини та незалежні та розподілені за законом та відповідно. Чи будуть незалежними випадкові величини та ?

7.35 Випадкова величина має функцію розподілу . В серії з незалежних випробувань значення випадкової величини розмістили в порядку зростання . Знайти функції розподілу випадкових величин та .

7.36 Випадкова величина розподілена за законом . Знайти розподіл густини ймовірності випадкової величини , якщо .

7.37 Випадкова величина розподілена за законом . Знайти розподіл густини ймовірності випадкової величини , якщо .

8.1 Випадкова величина розподілена за гіпергеометричним законом. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.2 Випадкова величина розподілена за біноміальним законом. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.3 Випадкова величина розподілена за геометричним законом. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.4 Випадкова величина розподілена за від’ємним біноміальним законом. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.5 Випадкова величина розподілена за законом Пуассона. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.6 Випадкова величина розподілена за показниковим законом. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.7 Випадкова величина розподілена за законом . За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.8 Випадкова величина розподілена за законом . За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.9 Випадкова величина розподілена за законом . За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.10 Випадкова величина розподілена за законом . За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.11 Випадкова величина розподілена за законом Стьюдента. За означенням обчислити математичне сподівання та дисперсію випадкової величини .

8.12 Площина розграфлена паралельними прямими, відстань між якими дорівнює . На площину кидають голку довжиною . Знайти математичне сподівання кількості перетинів голки з прямими.

8.13 Площина розграфлена паралельними прямими, відстань між якими дорівнює . На площину кидають випуклий??? замкнений контур довжиною , найбільший розмір якого . Знайти ймовірність перетину такого контуру з однією із прямих.

8.14 Якій умові повинні задовольняти незалежні випадкові величини та , щоб ?

8.15 Дискретна випадкова величина приймає тільки додатні значення, найбільше з яких дорівнює . Довести, що

та .

8.16 Розподіл випадкового вектора заданий за допомогою таблиці

Знайти математичне сподівання та дисперсію випадкової величини .

8.17 У випадкового вектора , , , , коефіцієнт кореляції . Знайти математичне сподівання та дисперсію випадкової величини .

8.18 Розподіл випадкового вектора заданий за допомогою таблиці