§ 2.8. Нечеткие выводы

Нечеткие выводы, нечеткие или приближенные рассуждения - это наиболее важный метод в нечеткой логике. Выводы а четком искусственном интеллекте охватывали как частный случай все нечеткие выводы, поэтому экспертные системы, построенные на четкой методологии ИИ, можно считать частным случаем нечетких экспертных систем (ЭС). Но и в нечетких ЭС, применяя на этапе исследований помимо правил четкие выводы с помощью фреймов или других методов, во многих случаях изучают также возможность их расширения до уровня нечетких выводов. Однако почти все реально работающие прикладные системы, активно использующие промежуточные нечеткие оценки, в настоящее время либо системы, основанные на правилах, а именно нечетких продукционных правилах, либо реализационные системы, использующие нечеткие отношения.

В ЭС на четкой методологии информация представима в виде системы условных высказываний, устанавливающих взаимосвязь между значениями входных и выходных параметров процесса подготовки принятия решений. Если в зависимости от возможных значений входных параметров делается вывод о значениях выходного параметра, то такую систему высказываний называют системой L⁽¹⁾ - типа. Данную систему представим в виде:

(2.10)

где m - число высказываний; A_j () - высказывание, отражающее входную ситуацию (значение входного параметра);B_j - высказывание, отражающее четкую выходную ситуацию (четкое значение выходного параметра или конкретные варианты решений задачи).

В случае, когда в зависимости от возможных значений выходной (B_j) ситуации экспертом делается предположение о возможной входной ситуации (A_j) (о возможных значениях входных параметров), систему высказываний называют системой L⁽²⁾ -типа. Представим ее в виде:

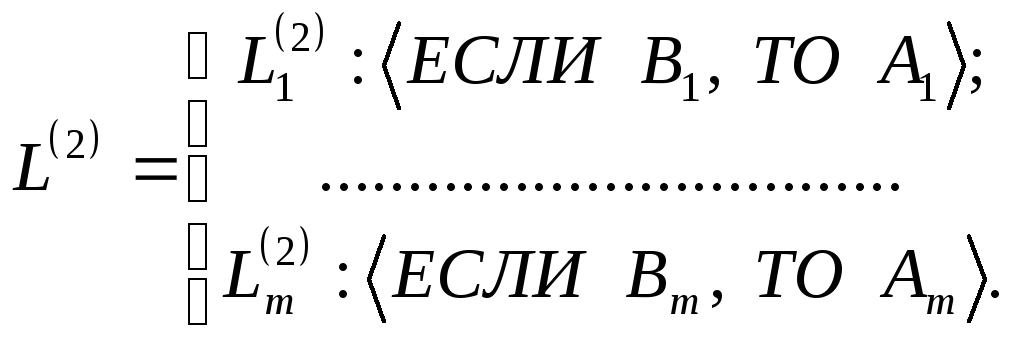(2.11)

Системы высказываний называются однозначными, если выполняются следующие условия:

для системы L⁽¹⁾ -типа;

для системы L⁽²⁾ -типа.

Система высказываний называется неизбыточной, если:

.

Пусть W - множество всех входных ситуаций процесса принятия решений. Систему высказываний называют полной, если выполняются условия:

для системы L⁽¹⁾ -типа;

для системы L⁽²⁾ -типа,

где P_W -входной параметр процесса принятия решения.

Иначе говоря, для любой входной ситуации существует экспертное высказывание, устанавливающее взаимосвязь между данной входной и некоторой выходной ситуациями.

При задании экспертной информации системой высказываний L⁽¹⁾ -типа выбор решения основывается на правиле modus ponens, а в случае задания системой L⁽²⁾ - типа - индуктивной схемой вывода.

Пусть A и B - произвольные четкие высказывания. Согласно правилу modus ponens из высказываний <ЕСЛИ A, ТО B> и A выводимо высказывание B. Формальное правило modus ponens запишется в виде:

Согласно индуктивной схеме вывода из высказываний <ЕСЛИ A, ТО B> и A следует правдоподобность высказывания B. Формально индуктивная схема вывода запишется в виде:

В общем случае, когда не известны даже нечеткие полезности вариантов решения, рекомендуется применять нечеткие выводы или приближенные рассуждения (наиболее важный метод в нечеткой логике) для принятия решений в неопределенной ситуации.

Нечеткий вывод - получение нового заключения из правил вывода, которые хранятся в базе знаний системы ИИ, и заданных фактов.

Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме «ЕСЛИ-ТО» и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:

1) Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.

2) Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечетких правил.

Системы высказываний в этом случае могут быть представлены следующим образом:

(Знание) ЕСЛИ x есть A, ТО y есть B,

(Факт)x есть A',

(Вывод) y есть B' (восходящий нечеткий вывод);

(Знание) ЕСЛИ x есть A, ТО y есть B,

(Факт) y есть B',

(Вывод)x есть A' (нисходящий нечеткий вывод),

где A,A',B,B' - нечеткие множества, причем , , где X - полное (универсальное) множество;

- степень принадлежности x_i множеству A, ,, , аналогично определены A' и B', .

Нечеткие множества A,A',B,B' можно рассматривать как векторы, записав их в следующем виде:

, ,

, ,

, ,

, .

Если A - причина, а B - следствие (результат), то знание отражает нечеткое причинное отношение предпосылки и заключения, поэтому назовем егонечетким отношением и обозначим через R:

R =,

где называется нечеткой импликацией.

R можно рассматривать как нечеткое множество на прямом произведении полного пространства предпосылокX и полного пространства заключений Y. Таким образом, процесс получения нечеткого результата вывода B' с использованием данных наблюдения A' и знания можно представить в виде:

. (2.12)

Здесь называетсякомпозиционным правилом нечеткого вывода (или правилом свертки). Если использовать векторную форму записи для A,A',B,B' (3) и записать R в виде матрицы:

,

то результат вывода B' представляется в следующем виде:

или , где- операцияMIN, алгебраическое произведение или другая операция.

Чаще всего используется операция MIN. Имеется несколько операций для получения нечеткого отношения:

; ;.

Например, нечеткий вывод с применением максиминной композиции в качестве композиционного правила нечеткого вывода и операции минимума в качестве нечеткой импликации можно представить:

.

Для анализа эффективности правил нечеткого условного вывода предлагается воспользоваться рядом критериев для F-условного логического вывода, смысл которых заключается в том, что они дают возможность проверить насколько то или иное правило нечеткого условного вывода удовлетворяет человеческой интуиции при приближенных рассуждениях. Разработка правил условного логического вывода в данной задаче охватывает, в основном, три вида условных предложений:

Р₁=ЕСЛИ х есть А, ТО y есть В;

Р₂=ЕСЛИ х есть А, ТО y есть В, иначе С; (2.13)

Р₃=ЕСЛИ х₁ есть А₁ и х₂ есть А₂, и ... х_n есть А_n, ТО y есть В.

Для логического предложения Р₁ предлагается правило вывода:

Предпосылка 1: ЕСЛИ х есть А, ТО y есть В; (2.14)

Предпосылка 2: х есть А'.

Следствие: y есть В',

где А и А' - F-концепции, представленные как F-множества в универсуме U; В - F-концепция или F-множество в универсуме V.

Откуда В' является следствием, представленным как F-множество в V. Для получения логического следствия, с использованием правил нечеткого условного логического вывода, предпосылки 1 и 2 должны быть соответственно приведены к F-отношению вида R(A₁(x),A₂(y)) и унарному F-отношению типа R(A₁(x₁)). Здесь A₁(x) и A₂(y) определяются атрибутами x и y, которые принимают значения из универсумов U и V соответственно.

Тогда R(A₁(x))=А'. (2.15)

Для R(A₁(x),A₂(y)) можно записать следующие правила их определения.

1.Максиминное правило условного предложения

. (2.16)

2.Арифметическое правило условного предложения

. (2.17)

3.Мини-функциональное правило условного предложения

. (2.18)

Здесь - декартово произведение и объединение соответственно;A^-1 – инверсия нечеткого множества А; + - предельная сумма.

Таким образом, логическое следствие R(A₂(y)), которое является В' в (5), нетрудно представить в виде:

, ,

или ,

где - операция максиминной композицииF-множеств.

На основе этих зависимостей были получены правила для условного предложения вида Р₂:

;

; (2.19)

.

Тогда правила для условного предложения Р₃ будут иметь вид:

;

; (2.20)

.

Для анализа эффективности правил (2.13)...(2.20) предлагается воспользоваться рядом критериев для F-условного логического вывода, представленных в табл.2.2, смысл которых заключается в том, что они дают возможность проверить насколько то или иное правило нечеткого условного вывода удовлетворяет человеческой интуиции при приближенных рассуждениях.

Таблица 2.2

Критерии F-условного логического вывода

Критерии	Предпосылки и следствия
Критерий 1	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть А. ______________________________________ Следствие: y есть В.
Критерий 2-1	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть очень А. ______________________________________ Следствие: y есть очень В.
Критерий 2-2	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть очень А. ______________________________________ Следствие: y есть В.
Критерий 3	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть более или менее А. ______________________________________ Следствие: y есть более или менее В.
Критерий 4-1	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть не А. ______________________________________ Следствие: y – неизвестно.
Критерий 4-2	Предпосылка 1: ЕСЛИ х есть А, ТО y есть В. Предпосылка 2: х есть не А. ______________________________________ Следствие: y есть не В.