5. Энергия упругой деформации

Любое упруго деформированное тело обладает потенциальной энергией, так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.

Растяжение будем производить очень медленно, чтобы силу , с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе. Тогдагдек, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна

(8.12)

Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид

, (8.13)

если считать, что потенциальная энергия недеформированной пружины равна нулю.

Потенциальная энергия упруго деформированного стержня равна

, (8.14)

где – объем стержня.

Отношение энергии к тому объему, в котором она заключена, называетсяплотностью энергии u. Тогда – плотность энергии упругой деформации при растяжении (или сжатии).

Аналогично нетрудно получить, что плотность энергии деформации при сдвиге равна .

6. Кручение

Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, верхний конец ее закрепим, а к нижнему концу приложим закручивающие силы. Они создадут вращающий момент относительно продольной оси проволоки. При этом каждый радиус нижнего основания повернется вокруг продольной оси на угол . Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид

_, (8.15)

где – модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения.

Пусть имеется цилиндрическая трубка радиуса . Причем толщина ееочень мала по сравнению с радиусом. Площадь сечения трубки равна . Обозначим черезкасательное напряжение в том же основании. Тогда момент сил, действующий на это основание, будет. При закручивании совершается работа.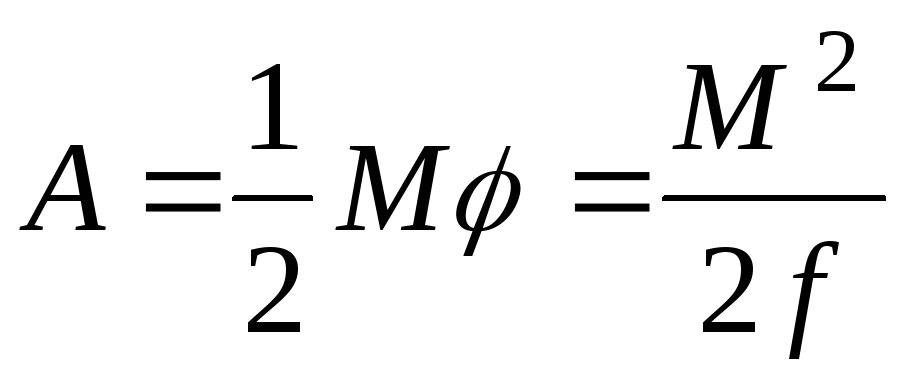

Разделим ее на объем трубки . Найдем плотность упругой энергии при деформации кручения

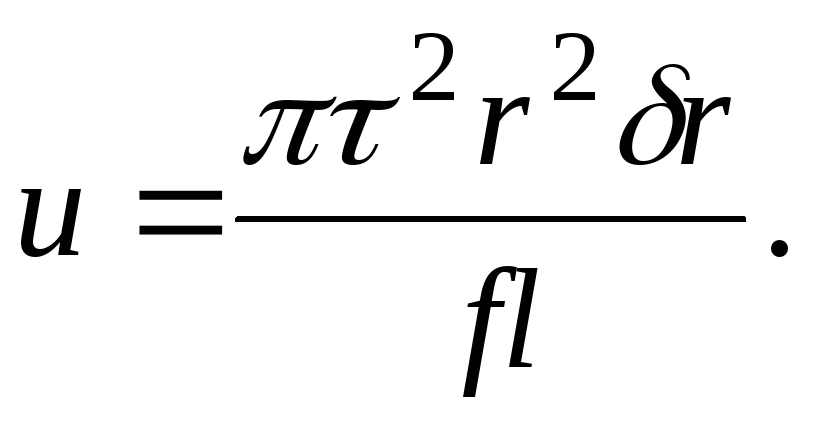(8.16)

Найдем эту же величину иначе.

Мысленно вырежем из трубки бесконечно короткую часть (рис.8.5).

Рис. 8.5

В результате кручения бесконечно малый элемент трубки ABDC перейдет в положение . Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна

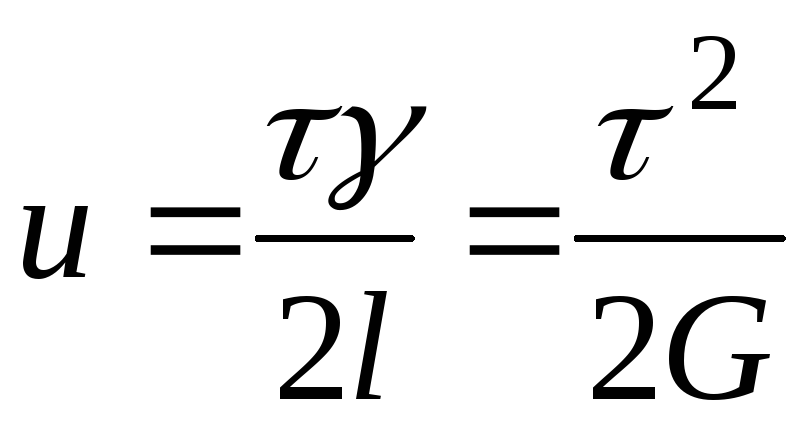(8.17)

Приравнивая его выражению (8.16), находим искомое соотношение

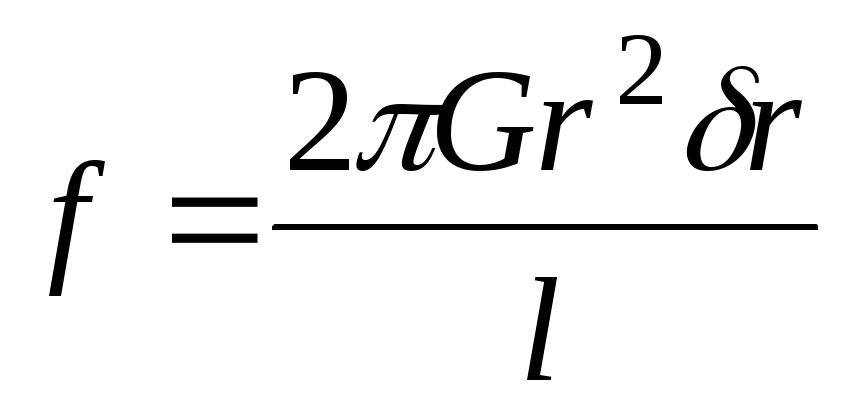(8.18)

Если стенка трубки имеет конечную толщину, то модуль найдется интегрированием последнего выражения по. Это дает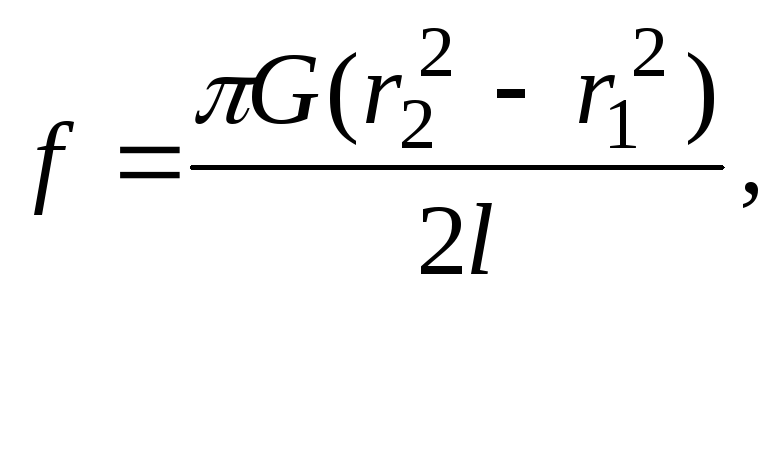 где – внутренний радиус трубки,– внешний радиус трубки.

Для сплошной проволоки радиуса _{модуль кручения .}

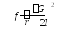Контрольные вопросы

1. Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.

2. Какова физическая сущность упругих сил?

3. Сформулируйте закон Гука? Когда он справедлив?

4. Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?

5. Что такое упругий гистерезис и упругое последействие?

6. Каков физический смысл модуля Юнга и модуля сдвига?

7. Что такое упругое последействие?

8. Выведите выражения для деформаций при всестороннем растяжении.

9. Что называется коэффициентом Пуассона?

10. Определите энергию деформированного тела.

11. Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.

12. Какой вид имеет закон Гука при кручении.

13. Выведите выражение для модуля кручения.