3. Поступательное движение твердого тела

Простейший случай движения твердого тела – поступательное движение, т.е. такое движение, при котором все точки твердого тела движутся по подобным траекториям или любая прямая, связанная с телом, остается при его движении параллельной самой себе (рис. 7.1).

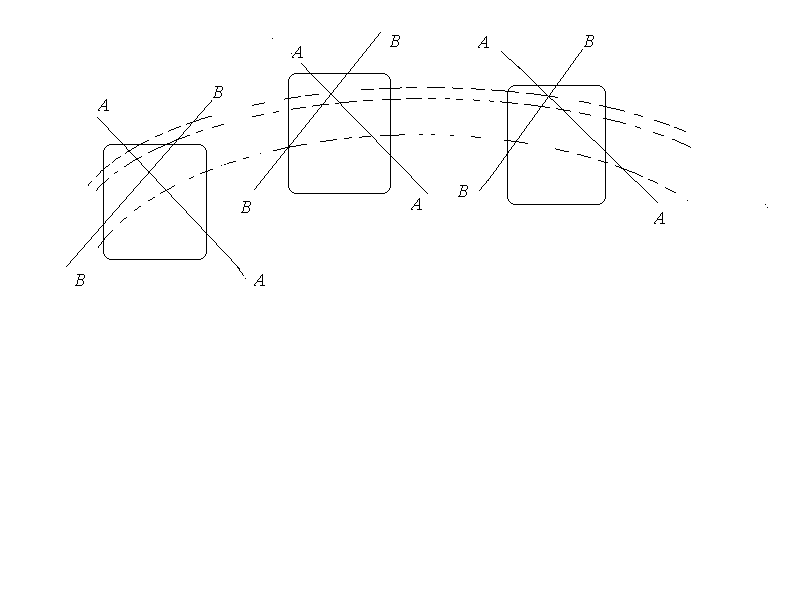
Рис.7.1

Обозначим цифрами 1 и 2 две произвольные точки тела, характеризуемые радиусами-векторами и. Пусть– вектор, проведенный из точки 1 в точку 2 (рис.7.2). Расстояние между рассматриваемыми точками неизменно, поэтому. Оно связано с радиусами-векторами точек соотношением. Продифференцировав по времени, получим, что, т.е..

Аналогично имеем .

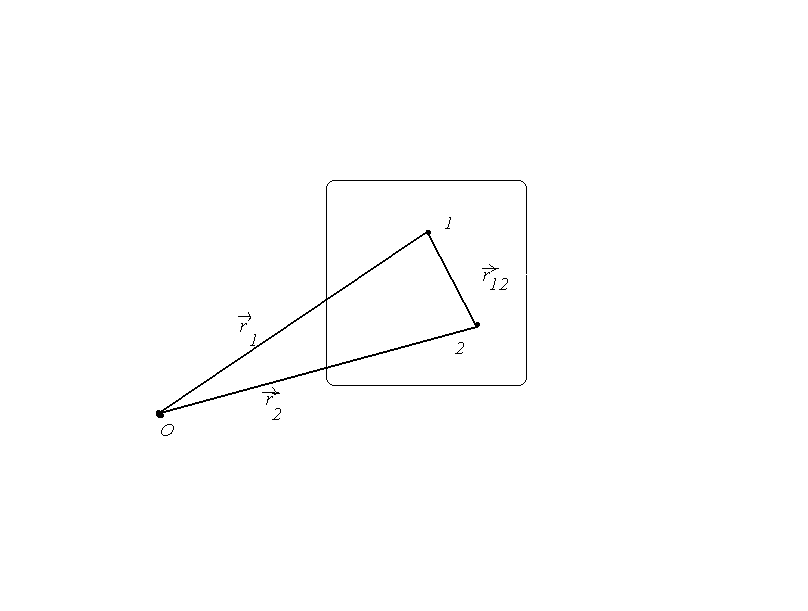Рис.7.2

Таким образом, все точки тела получают за один тот же промежуток времени равные по модулю и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Отсюда следует, что при поступательном движении траектории всех точек идентичны и могут быть совмещены параллельным переносом. Поэтому достаточно определить движение одной из точек тела (например, его центра масс) для того, чтобы охарактеризовать полностью движение всего тела.

Следует также отметить, что в случае поступательного движения уравнение (7.6) будет определять ускорение не только центра масс, но и любой другой точки тела.

4. Вращательное движение твердого тела

При вращательном движении все точки тела движутся по подобным траекториям, центры которых лежат на одной и той же прямой, называемой осью вращения(рис.7.3). Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.

O

φ Q

P

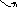
O

Рис.7.3.

Положение вращающегося тела может быть определено двугранным углом , между двумя полуплоскостями, проходящими через ось вращения. Одна плоскостьнеподвижна относительно системы координат, другаясвязана с телом и вращается вместе с ним. Знакопределяют по правилу правого винта.

Закон вращения твердого тела определяется уравнением:

(7.7)

Следуя кинематике движения точки по окружности, рассмотренной в предыдущих разделах, вращательное движение твердого тела можно характеризовать угловой скоростью, т.е. скоростью изменения угла поворота:

(7.8)

Чтобы охарактеризовать не только быстроту вращения, но также и ориентацию оси вращения в пространстве и направление вращения, вводят векторную величину , модуль которой определяется формулой (7.8). Направлен векторвдоль оси вращения, причем так, что направление вращения и направлениеобразуют правовинтовую систему: если смотреть вслед вектору, вращение представляется происходящим по часовой стрелке. (Рис.7.4). Определенная таким образом векторная величинаназываетсяугловой скоростью тела.

ω

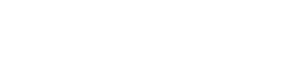
d^φ

R

R

Рис.7.4.

Поскольку направление угловой скорости определяется условно, является псевдовектором.

Быстрота изменения угловой скорости со временем характеризуется угловым ускорением, т.е.:

(7 .9)

Как и угловая скорость, угловое ускорение является псевдовектором.

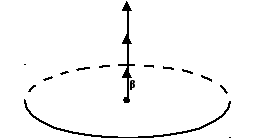
Как видно из формулы (7.9), направление определяется направлением изменения угловой скорости. Если угловая скорость растет со временем, т.е. вращение ускоренное, направленияисовпадают, если же вращение замедленное, направленияипротивоположные (рис. 7.5).

ω₂

ω₁

Рис. 7.5. а)

ω₁

ω₂

β

Рис. 7.5. б)

Найдем связь векторов между ис величинамии. Возьмем какую-либо произвольную точку этого тела, отстоящую от оси вращения на расстоянииR. Ранее было показано, что линейная и угловая скорости точки связаны соотношением

(7.10)

Будем определять положение точек тела с помощью радиус-вектора , проведенного из точки, лежащей на оси вращения. На рис.7.6 видно, что. Постановка этого значения в (7.6) дает.

Это равенство и показанные на рис. 7.6 взаимные направления векторов ,идают основания представитьв виде векторного произведенияна:

(7.11)

Рис.7.6

Связи модулей нормального и тангенциальногоускорений с угловым ускорением и угловой скоростью имеют вид

(7.12)

Заметим, что последняя формула в (7.12) справедлива для случая, когда ось вращения, а, следовательно, и вектор , не изменяет направления в пространстве.