8. Гравитационные силы (силы тяготения)

Изучая движение небесных тел и падение тел в земных условиях, И.Ньютон установил закон всемирного тяготения, который гласит: тело массой действует на находящееся от него на расстоянииr тело массой с силой, величина которой пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними, т.е.

(4.10)

В формуле (4.10) называется гравитационной постоянной.

Сила направлена по линии, соединяющей тела, и является силой притяжения.

Формулу (4.10) можно написать в виде

(4.11)

В этой формуле – вектор, проведенный от первого тела ко второму. Его модуль , тогда абсолютная величина силы в формулах (4.10) и (4.11) одинакова. Направление этой силы совпадает с направлением вектора, т.е. эта сила направлена по линии, соединяющей тела от второго тела к первому.

Приведенные формулы справедливы как для материальной точки, так и для произвольного тела. В последнем случае расстояние отсчитывается от центров этих тел.

Величина гравитационной постоянной впервые была измерена Кавендишем в 1798 г. с помощью крутильных весов. Физический смысл её заключается в том, что она равна выраженной в ньютонах силе тяготения между точечными телами массой в 1 кг каждая, находящимися на расстоянии 1 м друг от друга. Значение этой величины очень мало. Поэтому малы и силы тяготения. Чтобы силы тяготения были заметны, необходимо, чтобы хотя бы одно из взаимодействующих тел имело огромную массу. Так, сила тяготения между Землей и Луной имеет порядок Н, а между двумя почти соприкасающимися молекулами кислорода –Н.

Данный закон доказывает, что взаимодействие между телами осуществляется через особый вид материи – посредством гравитационного поля.

Отличительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их массы, одинаковое ускорение. Действительно, если применить формулу для случая взаимодействия земного шара с телами, расположенными вблизи земной поверхности, то выражение силы тяготения тел к Земле можно представить в виде , где– масса Земли,R – её радиус, – масса тела.

C другой стороны, _, где – ускорение свободного падения тел вблизи земной поверхности. Сравнивая последние формулы, получим.

Так как значения постоянных, входящих в последнюю формулу, известны, ясно, что все тела вблизи поверхности Земли падают с одинаковым ускорением, равным . Строго говоря, это ускорение зависит от широты и высоты места.

Следует отметить ещё одну особенность – особенность массы. Согласно закону всемирного тяготения масса имеет смысл меры силы тяготения (гравитационная масса). Ранее мы говорили, что масса – это мера инертности (инертная масса). Хотя по физическому смыслу эти массы различаются, опыт показывает, что численные значения их отличаются незначительно.

9. Сила тяжести и вес. Невесомость

Вблизи поверхности Земли все тела падают с одинаковым ускорением. Отсюда вытекает, что в системе отсчета, связанной с Землей, на всякое тело действует сила

(4.12)

Эта сила называется силой тяжести. Она приближенно равна силе гравитационного притяжения тела к Земле. Это различие не превышает 0,36 % и оно связано тем, что система отсчета, связанная с Землей, не вполне инерциальна.

Если подвесить тело или положить его на опору, оно будет покоиться относительно Земли (Рис. 4.2). В этом случае сила тяжести уравновешивается силой , которую называютреакцией подвеса или опоры. Реакциями называются силы, с которыми на данное тело действуют тела, ограничивающие его движение. По третьему закону Ньютона тело действует на подвес или опору с силой , которую называют весом тела.

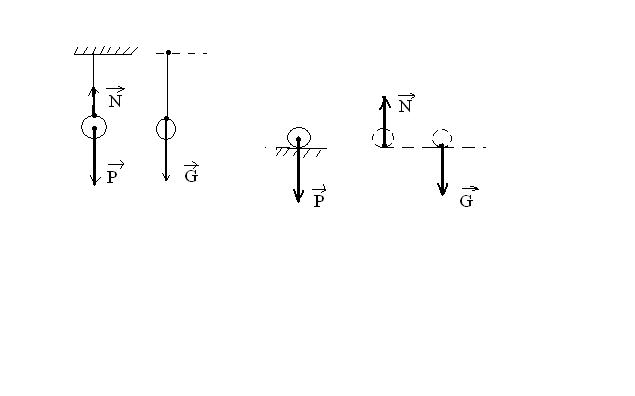
а) б)

Рис. 4.2.

Таким образом, вес тела – это сила, с которой тело действует на подвес или опору вследствие гравитационного притяжения к Земле.

Поскольку силы иуравновешивают друг друга, выполняется условие.

Вес есть сила, с которой тело действует на подвес (или опору), аесть сила, с которой повес (или опора) действует на тело. Согласно третьему закону Ньютона должно выполняться соотношение.

Сравнение обоих соотношений дает, что

(4.13)

Таким образом, вес и сила тяжести равны друг другу. Однако приложены они к разным телам – вес к подвесу (или опоре), сила тяжести – к самому телу.

Равенство (4.13) имеет место только в том случае, когда подвес или опора (а, следовательно, и тело) покоится относительно Земли (или движется без ускорения). Если же точка крепления подвеса или опора движется с ускорением, вес перестает быть равным силе тяжести.

Рис.4.3. Определение веса тела.

Для пояснения сказанного полезно рассмотреть показания весов, на которых стоит гиря. В неподвижном состоянии на гирю действуют две силы – сила тяжести и сила реакции опоры (весов), причем. Если весы движутся вниз с ускорениема (см. рис.4.3), то уравнение второго закона Ньютона, записанное в неподвижной системе координат1, имеет вид:

(4.14)

откуда (4.15)

Учитывая (4.14), вес гири

(4.16)

Очевидно, что при а = g , т.е. все свободно падающие тела ничего не весят, т.е. наступаетсостояние невесомости. Космический корабль, летящий на околоземной орбите с неработающими двигателями, движется, как и оборвавшийся лифт, с ускорением . Поэтому тела внутри корабля находятся в состоянии невесомости – они не оказывают давления на соприкасающиеся с ними тела. В частности, внутренние органы космонавта перестают оказывать давление на органы, расположенные ниже, а вес тела в целом перестает давить на кости скелета. Этим обуславливается специфическое физиологическое ощущение невесомости.

Сила тяжести на поверхности Земли не является постоянной по двум причинам: во-первых, Земля, как известно, не является идеальным шаром (она сплюснута на полюсах так, что на полюсах g больше, чем на экваторе); во-вторых, вследствие суточного вращения Земли, на все тела на ее поверхности (за исключением географических полюсов) действует центростремительное ускорение a_ц = соs, направленное в ту же сторону, что и g. Поэтому вес тел будет меньше там, где радиус вращения больше, т.е. на экваторе тела имеют наименьший вес.

r  R

Рис.4.4. Изменение радиуса вращения.