
- •Министерство образования и науки
- •Содержание
- •Предисловие
- •Программа курса “Механика”
- •Место дисциплины в учебном процессе и виды учебной работы
- •Распределение учебных часов
- •Учебно-тематический план
- •Содержание курса
- •Примерная тематика семинарских занятий
- •Вычислительный эксперимент
- •Средства обеспечения дисциплины
- •Рекомендуемая литература
- •Лекция №1. Введение
- •1. Предмет физики, её связь с другими естественными науками
- •2. Методы физических исследований
- •3. Роль модельных представлений в физике
- •4. Физические величины, их измерение и оценка точности и достоверности полученных результатов
- •5. Системы единиц физических величин
- •Контрольные вопросы
- •Лекция №2. Кинематика материальной точки при прямолинейном движении
- •1. Кинематические законы движения материальной точки
- •Зависимость (2.3)
- •2. Скорость и ускорение при прямолинейном движении
- •Контрольные вопросы
- •Лекция №3. Кинематика материальной точки при криволинейном движении
- •1. Скорость материальной точки при криволинейном движении
- •2. Ускорение материальной точки при криволинейном движении
- •3.Ускорение при движении материальной точки по окружности
- •4. Кинематика вращательного движения материальной точки
- •Контрольные вопросы
- •Лекция №4. Динамика материальной точки
- •1. Первый закон Ньютона
- •2. Масса
- •3. Сила
- •4. Второй закон Ньютона
- •5. Третий закон Ньютона
- •6. Импульс. Общая формулировка второго закона Ньютона
- •7. Виды взаимодействий тел
- •8. Гравитационные силы (силы тяготения)
- •9. Сила тяжести и вес. Невесомость
- •10. Силы трения
- •Контрольные вопросы
- •Лекция №5. Динамика системы материальных точек
- •1. Центр масс системы материальных точек
- •2. Закон сохранения импульса
- •Движение каждой точки описывается вторым законом Ньютона:
- •3. Движение тел с переменной массой. Реактивное движение
- •4. Задача двух тел. Приведенная масса
- •Контрольные вопросы
- •Лекция №6. Законы сохранения
- •1. Работа
- •2. Энергия и работа
- •3. Кинетическая энергия и работа
- •4. Потенциальная энергия
- •5. Закон сохранения и превращения механической энергии
- •6. Соударение двух тел
- •7. Момент силы относительно неподвижного центра
- •8. Момент импульса относительно неподвижного центра
- •9. Закон сохранения момента импульса
- •10. Законы сохранения и симметрия пространства и времени
- •Контрольные вопросы
- •Лекция №7. Механика твердого тела
- •1. Понятие об абсолютно твердом теле
- •2. Твердое тело как система материальных точек
- •3. Поступательное движение твердого тела
- •4. Вращательное движение твердого тела
- •5. Плоское движение твердого тела
- •6. Момент силы относительно оси
- •7. Момент пары сил
- •8. Второй закон Ньютона для вращающегося твердого тела
- •9. Момент инерции твердого тела
- •10. Теорема Штейнера
- •11. Закон сохранения момента импульса при вращательном движении
- •12. Кинетическая энергия вращающегося тела
- •13. Кинетическая энергия тела при плоском движении
- •14. Свободные оси вращения
- •15. Гироскоп
- •16. Степени свободы и связи абсолютно твердого тела
- •17. Условия равновесия твердого тела. Виды равновесия
- •18. Центр тяжести
- •Контрольные вопросы
- •Лекция №8. Механика деформируемых тел
- •1. Упругие силы
- •2. Виды упругих деформаций
- •3. Упругие и пластические деформации. Предел упругости и предел прочности
- •4. Всестороннее растяжение и сжатие
- •5. Энергия упругой деформации
- •Потенциальная энергия упруго деформированного стержня равна
- •6. Кручение
- •Контрольные вопросы
- •Лекция №9. Механика жидкостей и газов
- •1. Механические свойства жидкостей и газов
- •2. Гидростатика
- •Кажущийся вес тела
- •3.Гидродинамика
- •4. Описание движения жидкостей. Уравнение неразрывности струи
- •5. Уравнение Бернулли
- •6. Вязкость
- •7. Ламинарное и турбулентное течения
- •8. Течение вязкой жидкости в круглой трубе. Формула Пуазейля
- •9. Движение тел в жидкостях и газах. Закон Стокса
- •10. Истечение жидкости из отверстия
- •Контрольные вопросы
- •Лекция №10. Движение в неинерциальных системах отсчета
- •1. Неинерциальные системы отсчета
- •2. Силы инерции
- •3. Силы инерции при ускоренном поступательном движении системы отсчета
- •123 4. Силы инерции при равномерном вращательном движении системы отсчета. Центробежная сила инерции
- •5. Сила Кориолиса
- •Контрольные вопросы
- •Лекция №11. Механические колебания и волны
- •1. Гармонические колебания и их характеристики
- •2. Динамика колебательного движения
- •3. Гармонический осциллятор. Пружинный, физический и математический маятники
- •4. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •5. Сложение взаимно перпендикулярных колебаний
- •6. Свободные затухающие колебания
- •7. Вынужденные колебания
- •8. Амплитуда и фаза вынужденных колебаний. Резонанс
- •9. Автоколебания
- •10.Распространение колебаний в однородной упругой среде
- •11. Уравнение плоской и сферической бегущей волны. Фазовая скорость. Волновое уравнение
- •12. Принцип суперпозиции. Групповая скорость
- •13.Энергия упругой волны
- •14. Интерференция волн
- •15. Стоячие волны
- •16. Характеристика звуковых волн
- •17. Эффект Доплера в акустике
- •18. Ультразвук и eго применение
- •Контрольные вопросы
- •Лекция №12. Всемирное тяготение
- •1. Законы Кеплера и закон всемирного тяготения
- •2. Гравитационная масса
- •3. Поле тяготения и его напряженность
- •4. Работа в поле тяготения. Потенциал поля тяготения
- •5. Космические скорости
- •6. Принцип эквивалентности гравитационных сил и сил инерции
- •Контрольные вопросы
- •Лекция № 13. Элементы специальной теории относительности
- •1. Преобразования Галилея. Механический принцип относительности
- •2. Постулаты специальной (частной) теории относительности
- •3. Преобразования Лоренца
- •4. Следствия из преобразований Лоренца
- •5. Интервал между событиями
- •6. Основной закон релятивистской динамики материальной точки
- •7. Взаимосвязь массы и энергии
- •Контрольные вопросы
- •Фатыхов Миннехан Абузарович Механика
2. Ускорение материальной точки при криволинейном движении
В общем
случае (и чаще всего) при движении
материальной точки скорость меняется
как по величине, так и по направлению.
Пусть в момент времени
![]() материальная точка двигалась со скоростью
материальная точка двигалась со скоростью
![]() ,
а при
,
а при![]() – скоростью
– скоростью![]() .
Перенесем начало вектора скорости
.
Перенесем начало вектора скорости![]() из точки В в точку А, сохраняя величину
и направление вектора
из точки В в точку А, сохраняя величину
и направление вектора![]() .
Тогда приращение скорости
.
Тогда приращение скорости![]() (рис.3.3).
(рис.3.3).

 Δυτ
Δυτ



 υ1
υ1

 A
A

 Δv
Δv

ΔS

 B
B


 Δυn
υ2
Δυn
υ2
0
 υ2
υ2
Рис. 3.3.
Среднее ускорение на отрезке траектории между А и В:
![]() (3.10)
(3.10)
Величина вектора среднего ускорения показывает, как быстро (в среднем) происходит изменение скорости точки, а направление его совпадает с направлением вектора изменения скорости, т.е. направлено под углом к траектории в сторону её вогнутости.
Однако
знание перемещения и средней скорости
не дает достоверной информации о
характере движения в данной точке
пространства. Поэтому нужно уменьшить
промежуток времени. При его уменьшении
будет уменьшаться и величина вектора
приращения скорости, следовательно,
отношение (3.10) будет стремиться к
определенному пределу. Ускорением
(точнее мгновенным ускорением) материальной
точки в данной точке траектории в данный
момент времени называется предел
отношения (3.10) при
![]() :
:
 (3.11)
(3.11)
Из этого определения следует, что:
ускорение есть векторная величина;
ускорение направлено под углом к траектории в сторону её вогнутости;
ускорение представляет собой первую производную вектора скорости по времени;
ускорение представляет собой вторую производную радиус-вектора по времени; это следует из формул (3.11) и (3.3);
вектор ускорения можно представить в виде
![]() , (3.12)
, (3.12)
![]() ,
(3.13)
,
(3.13)
или
![]() ;
(3.14)
;
(3.14)
составляющие вектора скорости по координатным осям равны:
![]() ,
,
![]() ,
,![]() ;
(3.15)
;
(3.15)
величина ускорения равна
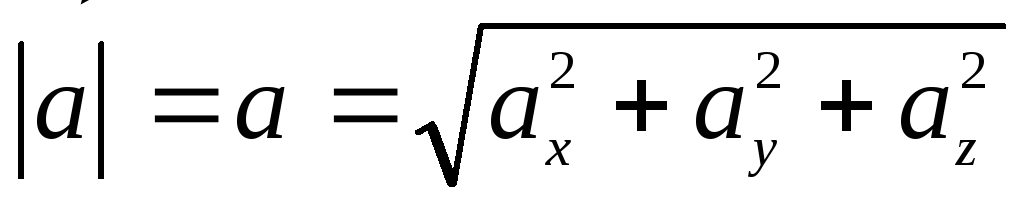 ;
(3.16)
;
(3.16)
для нахождения закона движения необходимо найти проекцию ускорения на оси координат по известным зависимостям проекций вектора скорости от времени, а затем интегрировать левую половину уравнений (3.15);
направление вектора ускорения совпадает с направлением вектора скорости только в случае ускоренного (или замедленного) прямолинейного движения.
Закон
движения материальной точки находится
из решения уравнений (3.15). Для примера
рассмотрим равноускоренное прямолинейное
движение, т.е.
![]() ,
где изменяется только скорость:
,
где изменяется только скорость:![]() ,
где
,
где![]() – единичный вектор скорости.
– единичный вектор скорости.
Из
этого выражения следует, что в случае
увеличения со временем скорости (т.е.
![]() ),
ускорение направлено так же, как скорость,
а модуль ускорения равен
),
ускорение направлено так же, как скорость,
а модуль ускорения равен![]() .
Если же скорость со временем уменьшается
(т.е.
.
Если же скорость со временем уменьшается
(т.е.![]() ),
направление ускорения противоположно
направлению скорости, а модуль ускорения
равен
),
направление ускорения противоположно
направлению скорости, а модуль ускорения
равен![]() .
.
Пусть движение происходит равноускоренно вдоль оси Ох, т.е. движение равноускоренное и прямолинейное. Тогда из первого уравнения (3.15) имеем:
![]()
Рассмотрим
подробнее, как меняется скорость при
криволинейном движении. Пусть материальная
точка за некоторый промежуток времени
![]() перемещается из положения А в
положение В с изменением скорости от
перемещается из положения А в
положение В с изменением скорости от![]()
![]() до
до![]() .
Перенесем вектор
.
Перенесем вектор![]() параллельно
самому себе так, чтобы его начало совпало
с точкой А. Соединим концы векторов
параллельно
самому себе так, чтобы его начало совпало
с точкой А. Соединим концы векторов![]()
![]() и
и![]() .
Тогда приращение векторов скорости
равно
.
Тогда приращение векторов скорости
равно![]() .
Отложим на векторе
.
Отложим на векторе![]() вектор, равный вектору
вектор, равный вектору![]() .
Следовательно, вектор
.
Следовательно, вектор![]() можно рассматривать как сумму двух
составляющих: как показано на рисунке,
обозначим их
можно рассматривать как сумму двух
составляющих: как показано на рисунке,
обозначим их![]() и
и![]() ,
т.е.
,
т.е.![]() .
Тогда среднее ускорение равно
.
Тогда среднее ускорение равно![]() .
.
Используя (3.11), из последнего выражения получим:
![]() , (3.17)
, (3.17)
где
![]() и
и![]() – соответственнонормальное и
тангенциальное ускорения. Причем в
пределе направления
– соответственнонормальное и
тангенциальное ускорения. Причем в
пределе направления![]()
![]() и
и![]() практически совпадают, следовательно,
вектор
практически совпадают, следовательно,
вектор![]() направлен так же, как и вектор
направлен так же, как и вектор![]() по касательной в каждой точке траектории,
а его значение определяют изменения
величины (модуля) скорости:
по касательной в каждой точке траектории,
а его значение определяют изменения
величины (модуля) скорости:
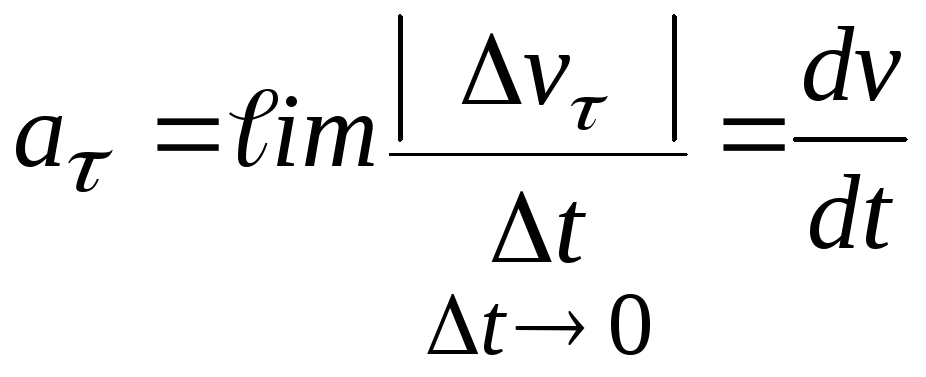 (3.18)
(3.18)
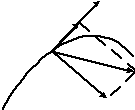
Нормальная
составляющая ускорения
![]() при этом окажется перпендикулярной
вектору скорости
при этом окажется перпендикулярной
вектору скорости![]() ,
направленному перпендикулярно касательной
к траектории, и показывать изменение
направления скорости (рис. 3.4).
,
направленному перпендикулярно касательной
к траектории, и показывать изменение
направления скорости (рис. 3.4).

V

ατ

α
α n
n
Рис.3.4
Величина (модуль) полного ускорения при его разложении на нормальную и тангенциальную составляющие равна:
![]() (3.19)
(3.19)
