Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций. Абсолютная трансформированная погрешность дифференцируемой функции , вызываемая достаточно малой погрешностью аргумента , оценивается величиной .

Если , то .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями аргументов оценивается величиной:

.

Если , то .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной , если дифференцируема и :

.

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности , то:

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

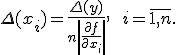
Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

Точное решение задачи легко найти:

Если компьютер работает при , то свободный член в исходном уравнении будет округлен до и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена привели, независимо от метода решения, к погрешности в решении .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

Общее решение имеет вид:

При заданных начальных данных точное решение задачи: , однако малая погрешность в их задании приведет к появлению члена , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

Его решение: , однако значение известно лишь приближенно: , и на самом деле .

Соответственно, разность будет:

Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке . Тогда должно выполняться условие:

Очевидно, что:

Отсюда можно получить требования к точности задания начальных данных при .

Таким образом, требование к заданию точности начальных данных оказываются в раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным. Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

является пара чисел .

Изменив правую часть системы на , получим возмущенную систему:

с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки , разность которых составляет .

В памяти машины эти же числа представляются в виде:

, причем и

Тогда:

Относительная ошибка при вычислении разности будет равна:

Очевидно, что , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением , тогда вместо получим , т.е. .

Следовательно, если , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.