4.4 Расчет режима линии электропередачи

В общем случае ЛЭП длинной 300-350 км представляется П-образной схемой замещения (рис. 3, а). На рис. 7 представлена П-образная схема замещения ЛЭП с обозначениями параметров электрического состояния, для которой определим параметры установившегося режима.

Рисунок 7 – Схема замещения линии электропередачи

Поперечные проводимости схемы в общем случае являются комплексными (активно-емкостными в рассматриваемом случае)

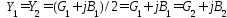. (18)

Рассмотрим характерные случаи расчета с учетом принятых обозначений на схеме замещения.

Расчет по данным в начале ЛЭП. Задано напряжение U₁ = const и мощность S₁ = const.

По известному напряжению U₁ вычислим ток источника питания

, (19)

Ток и мощность шунта в начале линии определяется по формуле

. (20)

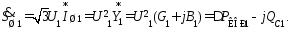(21)

Тогда в соответствии с первым законом Кирхгофа мощность в начале линии определяется по формуле

(22)

Аналогично ток в линии

. (23)

Этот же ток по данным в начале звена:

. (24)

Ток в продольном участке сети вызывает падение напряжения

(25)

на величину, которого в соответствии с указанным направлением тока напряжение в конце продольного участка меньше напряжения в начале

При протекании тока по продольному участку сети с сопротивлениемZ происходит потеря активной и реактивной мощностей, которые в соответствии с законом Джоуля – Ленца запишем

. (26)

Поток мощности в конце линии в соответствии с балансом мощности

, (27)

что позволяет вычислить ток в линии по данным в конце продольного звена

(28)

Отметим что (23), (28) дают одинаковый результат.

Далее вычисляем мощность шунта в конце линии ЛЭП

, (29)

и потребляемый шунтом ток

(30)

По балансовым соотношениям в конце ЛЭП находим мощность электропотребителя (доставляемую в приёмную систему)

(31)

и её ток

(32)

Выражение (32) можно записать в следующем виде

(33)

На этом расчёт параметров электрического режима, реализующий точную процедуру, заканчивается.

Расчет по данным в конце ЛЭП. Заданы в конце линии напряжение U₂ = const и мощность S₂ = const.

Как и в предыдущем случае, известны напряжение и мощность для одного конца схемы, что позволяет вычислить точно параметры электрического состояния в результате прямого расчета. В отличие от предыдущего случая расчет ведется от конца к началу линии (рис. 7).

Расчет режима ЛЭП при известном напряжении в начале U₁=const и мощности нагрузки в конце S₂= const. Данный случай является наиболее общим. Расчет параметров режима линии выполняется итерационным путем в два этапа.

Сначала зададим напряжение в конце линии U⁽⁰⁾₂, например, равным ожидаемому или номинальному. Тогда можно определить

приближенно ток нагрузки

(34)

Ток ветви проводимости (шунта)

(35)

и мощность ветви проводимости в конце линии

(36)

По балансовым соотношениям в узле 2 найдём мощности в конце линии

(37)

Ток линии

(38)

или можно вычислить в виде

(39)

Определим потери мощности в сопротивлениях линии

(40)

Значение мощности в начале линии

(41)

С учётом заданного напряжения позволяет уточнить ток продольного звена (39) в виде

(42)

По известному напряжению в начале линии находим ток поперечной ветви ( шунта )

(43)

и её мощность

(44)

По балансовым соотношениям первого закона Кирхгофа для узла 1 находим мощность, генерируемую источником питания

(45)

Тогда ток источника

(46)

или можно вычислить в виде

(47)

На этом первый этап (прямой ход) алгоритма заканчивается. На втором этапе (обратный ход) уточняется напряжение в конце линии

, (48)

С помощью составляющих вектора падения напряжения, вычисляемых по первым приближениям тока I⁽¹⁾ или мощности .

На этом заканчивается расчёт установившегося режима в первом приближении. Получив уточнённое напряжение в конце линии 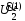, выполним весь расчёт вновь, но только в соответствующие формулы вместо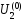подставим, и найдём новое значение напряженияв конце линии. Расчёт ведём до тех пор, пока не будет достигнута заданная точность расчётов, на практике ограничиваются одной или двумя итерациями. Анализируя характерные случаи расчёта режима ЛЭП, получим КПД линии электропередачи в процентах

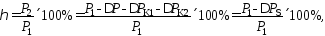(49)

которое зависит от потерь мощности нагрузочного и холостого режимов и снижается при их росте.

Из балансовых соотношений видно, что потери активной мощности в сопротивлении линии (нагрузочные потери), наряду с потерями на коронирование (потери холостого хода), уменьшают поступление активной мощности в приёмный конец линии, а зарядная мощность увеличивает поступление реактивной мощности в сеть. При этом часть реактивной мощности нагрузки, покрывается за счёт генерации реактивной мощности ёмкостью линии электропередачи.