
Praktika_III_Algoritmy
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Уфимский государственный авиационный технический университет
АЛГОРИТМЫ
ПРАКТИКУМ по дисциплине «Информатика»
Часть III
Уфа 2007
Составители: М.П. Карчевская, О.Л. Рамбургер
УДК 004.4 (07)
ББК 32.973-018.2(я7)
Алгоритмы: Практикум по дисциплине «Информатика». Часть III / Уфимск. гос. авиац. техн. ун-т; Сост.: М.П. Карчевская, О.Л. Рам-
бургер – Уфа, 2007. – 31 с.
Излагаются методические рекомендации для проведения третьего из пяти практических занятий по дисциплине «Информатика». Приводятся краткие теоретические сведения, описывается графический способ записи алгоритмов в соответствии с ГОСТ 19.701-90, описываются базовые алгоритмические структуры, приводятся примеры составления алгоритмов для решения типовых задач.
Предназначен для студентов, обучающихся по направлению подготовки дипломированного специалиста 140100 – « Теплоэнергетика» специальности 140101 – « Тепловые электрические станции», направлению 160300 – « Двигатели летательных аппаратов» специальности 160304 – « Авиационная и ракетно-космическая теплотехника», направлению 220300 – « Автоматизированные технологии и производства» специальности 220301 – « Автоматизация технологических процессов и производств» и направлению подготовки бакалавра 220200 – « Автоматизация и управление» и одобрены научнометодическими советами специальностей.
Библиогр.: 5 назв.
Рецензенты: канд. техн. наук доц. Каримов Р. Р. д-р техн. наук, проф. Кривошеев И. А.
© Уфимский государственный авиационный технический университет, 2007
|
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ................................................................................................................. |
4 |
|
1. |
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ................................................ |
5 |
2. |
СПОСОБЫ ЗАПИСИ АЛГОРИТМОВ .......................................................... |
7 |
3. |
БАЗОВЫЕ АЛГОРИТМИЧЕСКИЕ СТРУКТУРЫ..................................... |
8 |
4. |
МАССИВЫ......................................................................................................... |
25 |
СПИСОК ЛИТЕРАТУРЫ ..................................................................................... |
31 |
|
3
ВВЕДЕНИЕ
Тему «Алгоритм и его свойства» традиционно считают главной темой теоретической информатики, вводящей в обширные практические разделы алгоритмизации, различные языки программирования, а также методы программирования. Разработка алгоритмов и программ для решения прикладных задач является одним из важнейших остается наиболее стабильным компонентом подготовки студентов по различным направлениям.
4
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Для задач рассматриваемых в данном разделе (расчетные задача, имеющие решение) остановимся на интуитивно-содержательном оп-
ределении алгоритма: алгоритмом называется конечный набор точ- ных и понятных предписаний (правил, инструкций, команд), позво- ляющих за конечное число шагов механически решать конкретную задачу из определенного класса однотипных задач.
Свойства алгоритма. Любой разрабатываемый алгоритм должен удовлетворять ряду свойств, основные из которых приведены в табл. 1.1.
Таблица 1.1
|
Название свойства |
Значение свойства |
||
|
|
|
|
|
|
|
|
Пригодность алгоритма к целому классу однотипных |
|
Массовость |
задач, различающихся только исходным данными, ко- |
|||
торые могут выбираться из некоторой области, кото- |
||||
|
|
|
||
|
|
|
рая называется областью применимости алгоритма |
|
|
|
|
|
|
|
|
|
Каждое предписание «понимается» исполнителем ал- |
|
|
Детерминированность |
|
горитма однозначно и не оставляет места для двоякого |
|
|
(определенность) |
|
толкования. Благодаря этому свойству процесс реали- |
|
|
(однозначность) |
|
зации алгоритма не зависит от конкретного исполни- |
|
|
|
|
теля и может быть получено чисто механически. |
|
|
|
|
|
|
|
|
|
Процесс решения задачи определен в виде последова- |
|
|
|
|
тельности простых (или ранее определенных) шагов – |
|
Дискретность |
четко разделенных друг от друга предписаний. Вы- |
|||
|
|
|
полнение каждого из шагов начинается только после |
|
|
|
|
завершения предыдущего |
|
|
|
|
|
|
|
|
|
Алгоритм должен «выдавать» результат через конеч- |
|
|
Результативность |
|
ное число шагов. При этом либо достигается конечная |
|
|
|
цель (получено решение), либо выдаётся сообщение о |
||
|
|
|
||
|
|
|
невозможности решения задачи. |
|
|
|
|
|
|
|
|
|
Каждое предписание должно входить в систему ко- |
|
Понятность |
манд исполнителя. Он должен знать как его выпол- |
|||
нять. Нарушение этого принципа вызывает ошибки |
||||
|
|
|
||
|
|
|
типа "не понимаю", или "не могу выполнить". |
|
|
|
|
|
|
|
|
|
5 |
|
Объекты алгоритма. Решение любой задачи предполагает наличие реальных объектов – объектов задачи. Если выполнение алгоритма возложено на компьютер, необходима строгая формализация задачи. Она предполагает замену объектов задачи – объектами алгоритма, которые должны наследовать их атрибуты. При разработке алгоритма могут появиться и вспомогательные объекты не соответствующие никаким объектам задачи.
В практике программирования базовыми объектами являются константы, переменные, массивы и некоторые другие. Каждый объект в алгоритме должен фигурировать под своим именем. Имя это неизменно, фиксировано и уникально. Имена для объектов устанавливает автор алгоритма. Рекомендуется выбирать мнемонические имена, которые отражают суть объекта.
Константа – это объект алгоритма определенного типа (арифметического, символьного или др.), имеющий фиксированное, неизменяемое в данном алгоритме значение. Значение константы обычно определено в условии задачи и известно до начала разработки алгоритма.
Переменная – это объект алгоритма определенного типа (арифметического, символьного или др.), который в каждый момент исполнения алгоритма имеет единственное значение. К моменту использования переменной в алгоритме ее значение должно быть определено. В ходе выполнения алгоритма значение переменной может изменяться.
Массив – это объект алгоритма, в котором разрозненные переменные одного типа объединены в конечную упорядоченную по номеру (индексу) совокупность и имеют общее имя. Доступ к каждому элементу «напрямую» осуществляется по его номеру в массиве. По индексу массив строго упорядочен. В алгоритмах используются как одномерные, так и многомерные массивы. Для указания положения элемента в двумерном массиве используют два индекса – сначала номер строки, затем номер столбца. Массивы могут быть числовыми, символьными и др.
6
2.СПОСОБЫ ЗАПИСИ АЛГОРИТМОВ
Влюбом алгоритме всегда присутствует раздел инструкций (выполнения действий), который имеет одну точку входа (НАЧАЛО) и одну точку выхода (КОНЕЦ). Закодированная форма инструкции, несущая определенный смысл называется оператором.
Существует несколько способов записи алгоритмов, отличающихся друг от друга наглядностью, компактностью, степенью формализации. Наибольшее распространение получили: словесный, графический и программный.
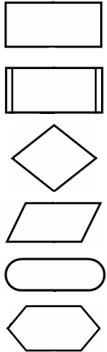
Графический способ записи предполагает использование определенных графических символов – блоков. Каждый блок предписывает выполнение определенных действий. Совокупность блоков образует схему алгоритма или блок-схему. Обозначение некоторых блоков в соответствии с ГОСТ 19.701-90 СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ ДАННЫХ И СИСТЕМ приведено в табл. 1.2.
Таблица 2.1
|
Наименование |
Обозначение |
|
Примечание |
|
|
|
символа |
символа |
|
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
||
|
|
|
|
|
Арифметический блок, определяющий |
|
|
Процесс |
|
|
действия, которые необходимо выпол- |
||
|
|
|
|
|
нить |
|
|
|
|
|
|
|
|
|
Предопределенный |
|
|
|
Обращение к подпрограмме |
|
|
процесс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логический блок, проверяющий ис- |
|
|
Принятие решения |
|
|
тинность или ложность некоторого ус- |
||
|
|
|
|
|
ловия |
|
|
|
|
|
|
||
|
Передача данных |
|
|
|
Ввод или вывод информации |
|
|
|
|
|
|
|
|
|
Прерывание |
|
|
Начало, конец, пуск, останов, вход в |
||
|
|
|
подпрограмму |
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Модификация |
|
|
|
Организация циклического процесса |
|
|
|
|
|
при известном количестве повторений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
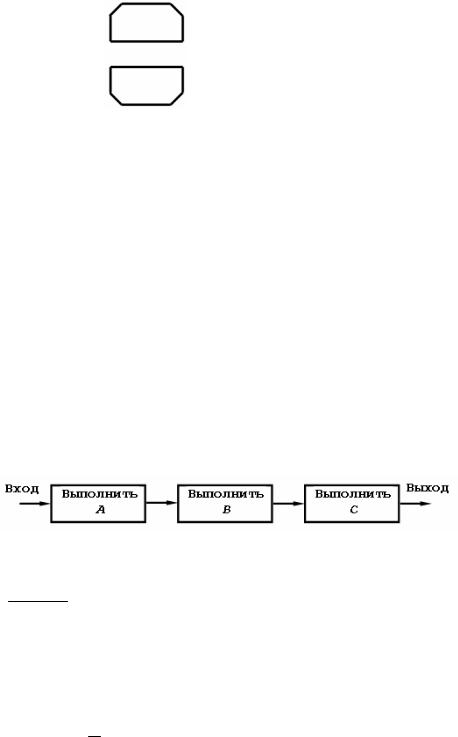
Окончание табл. 2.1
1 |
2 |
3 |
|
|
Начало и конец цикла. Условие поме- |
Граница цикла |
|
щают внутри символа в начале или |
|
конце в зависимости от расположения |
|
|
|
|
|
|
операции проверки условия |
|
|
|
Блоки соединяются линиями потока информации. Внутри блоков записываются выполняемые действия. Линии со стрелками определяют направление вычислений.
3. БАЗОВЫЕ АЛГОРИТМИЧЕСКИЕ СТРУКТУРЫ
Практически любой сложный алгоритм представляет собой комбинацию трех типов базовых алгоритмических структур: линей-
ного, разветвляющегося и циклического.
Линейные алгоритмические структуры. Линейный алгоритм
(следование) состоит из последовательности операций, выполняющихся только один раз в порядке их следования. Для графического способа записи линейной алгоритмической структуры используется блок «Процесс» (рис. 3.1).
Рис. 3.1. Линейная структура алгоритма
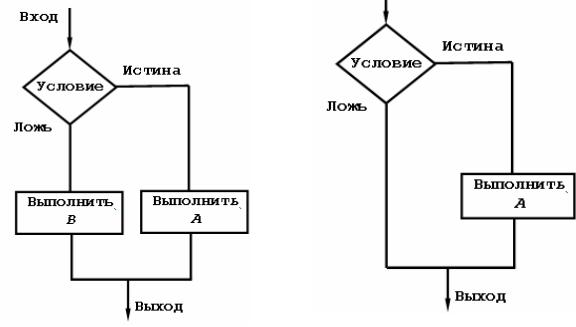
Пример 3.1. Вычислить значение функции
y = arctg(
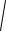 ax3 + b + ln(ax3 + b)). Записать алгоритм решения задачи
ax3 + b + ln(ax3 + b)). Записать алгоритм решения задачи
Объекты алгоритма: a, b, x, y числового типа. Словесная запись алгоритма:
1.Вычислить z = ax3 + b ;
2.Вычислить s = 
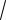 z ;
z ;
3.Вычислить t = ln(z) ;
4.Вычислить r = s + t ;
5.Вычислить y = arctg(r ).
Блок-схема алгоритма: представлена на рис. 3.4.
8
Разветвляющиеся алгоритмические структуры. Базовые раз-
ветвляющиеся структуры обеспечивают выбор одного из альтернативных путей работы алгоритма в зависимости от результата проверки какого-либо условия (логического выражения). Каждый из путей ведет к общему выходу, поэтому работа алгоритма будет продолжаться независимо от того, какой путь выбран. Для графического способа записи таких алгоритмов используется блок «Принятие решения», внутри которого записывается логическое выражение.
Разветвляющиеся алгоритмические структуры существуют в двух формах: полной «ЕСЛИ– ТО– ИНАЧЕ» (рис. 3.2) и сокращенной «ЕСЛИ– ТО» (рис. 3.3). Разветвляющая структура «ЕСЛИ – ТО» является частным случаем структуры «ЕСЛИ– ТО– ИНАЧЕ» и используется тогда, когда для одного из результатов проверки ничего предпринимать не надо.
Рис. 3.2. Разветвляющаяся структура |
Рис. 3.3. Разветвляющаяся структура |
«ЕСЛИ – ТО – ИНАЧЕ» |
«ЕСЛИ – ТО» |
Пример 3.2. Найти квадрат наибольшее из трех заданных чисел: a, b, c. Записать алгоритм решения задачи с помощью блок-схемы.
Объекты алгоритма: a, b, c, max числового типа. Словесная запись алгоритма:
1.Сравнить a и b. Если a >b, то принять max = a, в противном случае принять max = b.
9
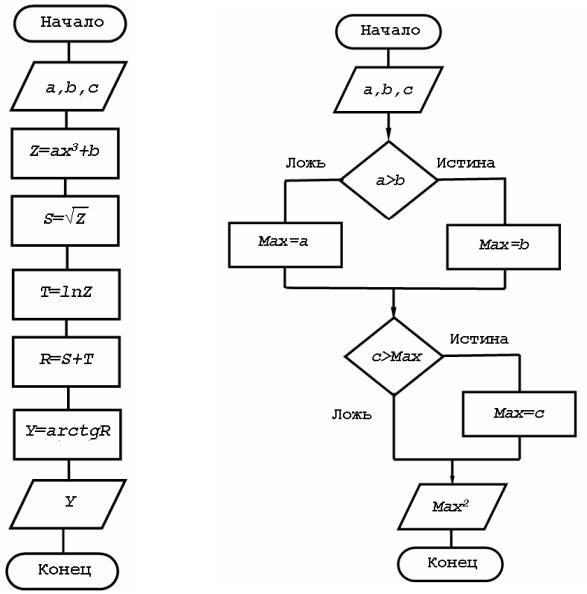
2.Сравнить c и max. Если c > max, то заменить max = c, в противном случае оставить max без изменений
3.Вычислить z = max2.
Блок-схема алгоритма: представлена на рис. 3.5.
Рис. 3.4. Блок-схема линейного |
Рис. 3.5. Блок-схема задачи с разветвлением |
алгоритма (пример 1.1) |
(пример 1.2) |
Пример 3.3. Найти корни квадратного уравнения ax 2 + bx + c = 0 . Записать алгоритм решения задачи с помощью блок-схемы.
Объекты алгоритма: a, b, c, x числового типа. Блок-схема алгоритма: представлена на рис. 3.6.
10
