Практикум_по_математике(2семестр)

§2. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ

2.1. Двойной интеграл. Двойной интеграл в полярных координатах

Двойной интеграл вычисляется сведением его к повторному в зависимости от заданной области интегрирования.

2.1.1. Двойной интеграл в декартовой системе координат.

Различают два основных вида области интегрирования:

1. Область интегрирования D ограничена слева и справа прямыми x = a и x = b (a < b), а снизу и сверху – непрерывными

В формуле вначале вычисляется внутренний интеграл, в котором х считается постоянной.

2. Область интегрирования D ограничена снизу и сверху прямыми y = c и y = d (c < d), а слева и справа – непрерывными

кривыми х = 1(у) и и х = 2(у) [ 1(у) 2(у)], каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 7).

61

Для такой области двойной интеграл вычисляется по формуле

Вначале вычисляется внутренний интеграл, в котором у считается постоянной.

Правые части в формулах называются двукратными (или повторными) интегралами.

В более общих случаях области интегрирования D путем их разбиения на части всегда можно свести к двум основным, рассмотренным выше.

Пример 2.1. Вычислить двойной интеграл:

(3x y)dxdy , D (x, y) |1 x 2, 2 y 3 .

D

Решение.

Пример 2.2. Вычислить двойной интеграл

(x y)dxdy,

D

если область D ограничена линиями

y = 2 – x2, y =2x – 1.

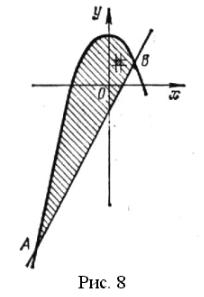
Решение. Построим область D. Первая линия – парабола с вершиной в точке С (0; 2), симметричная оси Оу. Вторая линия – прямая. Из совместного решения уравнений y = 2 – x2 и y=2x – 1 найдем координаты точек пересечения кривых (линий): это А(–3; 7) и В(1; 1) (рис. 8).

62

Решение. В данном примере область интегрирования D ограничена линиями

(рис. 9) (снизу – дуга окружности, сверху – парабола).

Изменим порядок интегрирования. Для этого заданную область представим в виде двух областей (второго вида): D1 ограниченной

слева и справа ветвями параболы x 1 y (0 y 1), и область D2, ограниченной

дугами окружности x 1 y2 (-1 y 0).

Имеем

63

Пример 2.4. Вычислить двойной интеграл

I (12x2 y2 16x3 y3 )dxdy,

Построим область интегрирования D. Первая линия – прямая, параллельная оси у, вторая линия – парабола с вершиной в точке (0;0), пересекающая первую линию в точке (1;1), третья линия – с началом в точке (0;0), пересекающая первую линию в точке (1;-1).

Отсюда интеграл перепишем в виде

Интегрируем по х:

2.1.2. Двойной интеграл в полярных координатах. Если область D

ограничена лучами, образующими с полярной осью углы 1 ,

2 , и кривыми 1 ( ) , 2 ( ) 1 ( ) 2 ( ) , то

64

Вычислить двойной интеграл, взятый по прямоугольным областям интегрирования D, заданным условиями в скобках:

Изменить порядок интегрирования:

65

Вычислить двойные интегралы:

x 2

245. D y 2 dxdy , где D – область, ограниченная прямыми x=2, y=x и

гиперболой xy=1.

246. С помощью перехода к полярным координатам (x=ρcosφ, y=ρsinφ) свести двойной интеграл к повторному:

66

2.2. Некоторые приложения двойного интеграла

1) S dxdy – вычисление площади области D;

D

2) объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f (x, y), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D, вычисляется по формуле

V f (x, y)dxdy

D

(геометрический смысл двойного интеграла); 3) если гладкая однозначная поверхность задана уравнением

z = f (x, y), то площадь этой поверхности выражается формулой

Sn 1 fx 2 (x, y) fy 2 (x, y)dxdy ,

D

где D есть проекция данной поверхности на плоскость хОу; 4) двойные интегралы

называются статистическими моментами пластинки D, плотность которой в каждой точке определяется функцией р(х, у), относительно осей Oy и Ox соответственно.

Пример 2.6. Вычислить площадь фигуры, ограниченной линиями x = 4y – y2, x + y = 6.

Решение. Построим область интегрирования (рис. 11). Первая кривая – парабола с вершиной в точке пересечения кривых А(4; 2).

Вторая – прямая линия, пересекающая оси в точках (0;6) и (6;0). Для определения границ области интегрирования найдем координаты точек пересечения заданных линий, решая систему уравнений x = 4y – y2 и x + y = 6. В результате получим А(4;2) и В(3;3). Область интегрирования на рис. 11 заштрихована. Таким образом,

67

Имеем

В рассматриваемом примере удобно перейти к полярным координатам. Уравнение окружности примет вид = asin , и интеграл для S преобразуется к виду

Вычислить объем тел, ограниченных заданными поверхностями.

247. Плоскостями координат, плоскостями x=4, y=4 и параболоидом вращения z=x2+y2+1.

69

250*. С помощью двойного интегрирования найти площадь области:

(x2+y2)2=2ax3.

Найти площадь указанной части данной поверхности:

251.Вычислить площадь той части плоскости 6x+3y+2z=12, которая заключена в первом октанте.

252.Найти площадь части конуса z x2 y2 , заключенной внутри цилиндра x2 + y2 = 2x.

Спомощью двойного интегрирования найти статический момент однородной плоской фигуры (плотность γ = 1):

253.Найти статический момент полукруга радиуса R относительно диаметра.

70