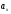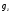8. Написать разложение вектора по векторам.
|
п/п |
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
1 |
-2 |
4 |
7 |
0 |
1 |
2 |
1 |
0 |
1 |
-1 |
2 |
4 | |||
|
2 |
6 |
12 |
-1 |
1 |
3 |
0 |
2 |
-1 |
1 |
0 |
-1 |
2 | |||
|
3 |
1 |
-4 |
4 |
2 |
1 |
-1 |
0 |
3 |
2 |
1 |
-1 |
1 | |||
|
4 |
-9 |
5 |
5 |
4 |
1 |
1 |
2 |
0 |
-3 |
-1 |
2 |
1 | |||
|
5 |
-5 |
-5 |
5 |
-2 |
0 |
1 |
1 |
3 |
-1 |
0 |
4 |
1 | |||
|
6 |
13 |
2 |
7 |
5 |
1 |
0 |
2 |
-1 |
3 |
1 |
0 |
-1 | |||
|
7 |
-19 |
-1 |
7 |
0 |
1 |
1 |
-2 |
0 |
1 |
3 |
1 |
0 | |||
|
8 |
3 |
-3 |
4 |
1 |
0 |
2 |
0 |
1 |
1 |
2 |
-1 |
4 | |||
|
9 |
3 |
3 |
-1 |
3 |
1 |
0 |
-1 |
2 |
1 |
-1 |
0 |
2 | |||
|
10 |
-1 |
7 |
-4 |
-1 |
2 |
1 |
2 |
0 |
3 |
1 |
1 |
-1 | |||
|
11 |
6 |
5 |
-14 |
1 |
1 |
4 |
0 |
-3 |
2 |
2 |
1 |
-1 | |||
|
12 |
6 |
-1 |
7 |
1 |
-2 |
0 |
-1 |
1 |
3 |
1 |
0 |
4 | |||
|
13 |
5 |
15 |
0 |
1 |
0 |
5 |
-1 |
3 |
2 |
0 |
-1 |
1 | |||
|
14 |
2 |
-1 |
11 |
1 |
1 |
0 |
0 |
1 |
-2 |
1 |
0 |
3 | |||
|
15 |
11 |
5 |
-3 |
1 |
0 |
2 |
-1 |
0 |
1 |
2 |
5 |
-3 | |||
|
16 |
8 |
0 |
5 |
2 |
0 |
1 |
1 |
1 |
0 |
4 |
1 |
2 | |||
|
17 |
3 |
1 |
8 |
0 |
1 |
3 |
1 |
2 |
-1 |
2 |
0 |
-1 | |||
|
18 |
8 |
1 |
12 |
1 |
2 |
-1 |
3 |
0 |
2 |
-1 |
1 |
1 | |||
|
19 |
-9 |
-8 |
-3 |
1 |
4 |
1 |
-3 |
2 |
0 |
1 |
-1 |
2 | |||
|
20 |
-5 |
9 |
-13 |
0 |
1 |
-2 |
3 |
-1 |
1 |
4 |
1 |
0 | |||
|
21 |
-15 |
5 |
6 |
0 |
5 |
1 |
3 |
2 |
-1 |
-1 |
1 |
0 | |||
|
22 |
8 |
9 |
4 |
1 |
0 |
1 |
0 |
-2 |
1 |
1 |
3 |
0 | |||
|
23 |
23 |
-14 |
-30 |
2 |
1 |
0 |
1 |
-1 |
0 |
-3 |
2 |
5 | |||
|
24 |
3 |
1 |
3 |
2 |
1 |
0 |
1 |
0 |
1 |
4 |
2 |
1 | |||
|
25 |
-1 |
7 |
0 |
0 |
3 |
1 |
1 |
-1 |
2 |
2 |
-1 |
0 | |||
|
26 |
11 |
-1 |
4 |
1 |
-1 |
2 |
3 |
2 |
0 |
-1 |
1 |
1 | |||
|
27 |
0 |
-8 |
9 |
0 |
-2 |
1 |
3 |
1 |
-1 |
4 |
0 |
1 | |||
|
28 |
8 |
-7 |
-13 |
0 |
1 |
5 |
3 |
-2 |
1 |
-1 |
0 |
1 | |||
|
29 |
2 |
7 |
5 |
1 |
0 |
1 |
1 |
-2 |
0 |
0 |
3 |
1 | |||
|
30 |
15 |
-20 |
-1 |
0 |
2 |
1 |
0 |
1 |
-1 |
5 |
-3 |
2 | |||
Общее решение однородной системы
Выразить через какую-нибудь фундаментальную систему решений.
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
1 |
-8 |
2 |
1 |
2 |
-2 |
-3 |
-7 |
2 |
1 |
11 |
-12 |
34 |
-5 |
|
2 |
7 |
2 |
-1 |
-2 |
2 |
1 |
-3 |
1 |
-1 |
-1 |
2 |
5 |
2 |
1 |
1 |
|
3 |
1 |
1 |
10 |
1 |
-1 |
5 |
-1 |
8 |
-2 |
2 |
3 |
-3 |
-12 |
-4 |
4 |
|
4 |
6 |
-9 |
21 |
-3 |
-12 |
-4 |
6 |
-14 |
2 |
8 |
2 |
-3 |
7 |
-1 |
-4 |
|
5 |
2 |
-1 |
2 |
-1 |
1 |
1 |
10 |
-3 |
-2 |
-1 |
4 |
19 |
-4 |
-5 |
-1 |
|
6 |
5 |
-2 |
3 |
-4 |
-1 |
1 |
4 |
-3 |
2 |
-5 |
6 |
2 |
0 |
-2 |
-6 |
|
7 |
12 |
-1 |
7 |
11 |
-1 |
24 |
-2 |
14 |
22 |
-2 |
1 |
1 |
1 |
-1 |
1 |
|
8 |
1 |
2 |
1 |
4 |
1 |
2 |
-1 |
3 |
1 |
-5 |
1 |
3 |
-1 |
-6 |
-1 |
|
9 |
2 |
-1 |
3 |
-1 |
-1 |
1 |
5 |
-1 |
1 |
2 |
1 |
16 |
-6 |
4 |
7 |
|
10 |
3/2 |
5/4 |
5/7 |
1 |
0 |
3/5 |
1/2 |
2/7 |
2/5 |
0 |
1/5 |
1/6 |
2/21 |
2/15 |
0 |
|
11 |
8 |
1 |
1 |
-1 |
2 |
3 |
-3 |
-2 |
1 |
-3 |
5 |
4 |
3 |
-2 |
5 |
|
12 |
1 |
3 |
-1 |
12 |
-1 |
2 |
-2 |
1 |
-10 |
1 |
3 |
1 |
0 |
2 |
0 |
|
13 |
7 |
-14 |
3 |
-1 |
1 |
1 |
-2 |
1 |
-3 |
7 |
5 |
-10 |
1 |
5 |
-1 |
|
14 |
1 |
2 |
3 |
1 |
-1 |
2 |
-2 |
-5 |
-3 |
1 |
3 |
-2 |
3 |
2 |
-1 |
|
15 |
1 |
1 |
1 |
-1 |
-1 |
2 |
1 |
-2 |
-1 |
-2 |
1 |
2 |
5 |
-2 |
-1 |
|
16 |
2 |
1 |
-3 |
1 |
-1 |
3 |
-1 |
2 |
-1 |
2 |
1 |
-2 |
5 |
-2 |
3 |
|
17 |
1 |
2 |
-3 |
10 |
-1 |
1 |
-2 |
3 |
-10 |
1 |
1 |
6 |
-9 |
30 |
-3 |
|
18 |
2 |
1 |
-1 |
7 |
5 |
1 |
-2 |
3 |
-5 |
-7 |
3 |
-1 |
2 |
2 |
-2 |
|
19 |
2 |
-2 |
-3 |
-7 |
2 |
1 |
11 |
-12 |
34 |
-5 |
1 |
-5 |
2 |
-16 |
3 |
|
20 |
3 |
1 |
-8 |
2 |
1 |
1 |
11 |
-12 |
-34 |
-5 |
1 |
-5 |
2 |
-16 |
3 |
|
21 |
1 |
3 |
-5 |
9 |
-1 |
2 |
-2 |
-3 |
-7 |
2 |
1 |
-5 |
2 |
-16 |
3 |
|
22 |
5 |
2 |
-1 |
3 |
4 |
3 |
1 |
-2 |
3 |
5 |
6 |
3 |
-2 |
4 |
7 |
|
23 |
1 |
3 |
-5 |
9 |
-1 |
2 |
-2 |
-3 |
-7 |
2 |
1 |
-5 |
2 |
-16 |
3 |
|
24 |
6 |
3 |
-2 |
4 |
7 |
7 |
4 |
-3 |
2 |
4 |
1 |
1 |
-1 |
-2 |
-3 |
|
25 |
3 |
-5 |
2 |
4 |
0 |
7 |
-4 |
1 |
3 |
0 |
5 |
7 |
-4 |
-6 |
0 |
|
26 |
1 |
11 |
3 |
-2 |
3 |
2 |
2 |
4 |
-1 |
3 |
1 |
1 |
5 |
-5 |
6 |
|
27 |
1 |
2 |
3 |
-2 |
1 |
1 |
2 |
7 |
-4 |
1 |
1 |
2 |
11 |
-6 |
1 |
|
28 |
6 |
3 |
2 |
3 |
4 |
4 |
2 |
1 |
2 |
3 |
2 |
1 |
1 |
1 |
1 |
|
29 |
3 |
2 |
4 |
1 |
2 |
3 |
2 |
-1 |
1 |
0 |
3 |
2 |
16 |
1 |
6 |
|
30 |
1 |
-1 |
1 |
-2 |
1 |
1 |
1 |
-2 |
-1 |
2 |
1 |
-3 |
4 |
-3 |
0 |
