
Содержание
-
Цель работы……………………………………………………………4
-
Теория метода……..….……………………………………………….4
-
Экспериментальная установка……….………………………………8
-
Порядок выполнения работы…………………………………………9
-
Требования к отчету…………………………………………………..9
-
Контрольные вопросы……………………………………………….10
Список литературы……………………………………………………..10 лабораторная работа № 123
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА КАПИЛЛЯРНЫМ МЕТОДОМ
-
Цель работы
1. Изучение внутреннего трения воздуха как одного из явлений переноса в газах.
2. Определение коэффициента вязкости воздуха и характеристик теплового движения его молекул.
-
Теория метода
Явления переноса – это процесс установления равновесия в системе путем переноса массы (диффузия), энергии (теплопроводность) и импульса молекул (внутреннее трение, или вязкость). Все эти явления обусловлены тепловым движением молекул.
При явлении вязкости наблюдается перенос импульса от молекул из слоев потока, которые двигаются быстрее, к более медленным. При протекании жидкости или газа в узкой прямолинейной цилиндрической трубе (капилляре) при малых скоростях потока течение является ламинарным, т.е. поток газа движется отдельными слоями, которые не смешиваются между собой. В этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.
Вследствие
хаотического теплового движения молекулы
непрерывно переходят из слоя в слой и
при столкновении с другими молекулами
изменяют импульсы своего направленного
движения. При переходе из слоя движущегося
с большей скоростью в слой, движущийся
с меньшей скоростью, молекулы переносят
в другой слой свой импульс направленного
движения. В «более быстрый» слой переходят
молекулы с меньшим импульсом. В результате
первый слой тормозится, а второй –
ускоряется. Опыт показывает, что импульс
dP,
который передается от слоя к слою через
поверхность площадью S
вдоль оси r,
перпендикулярной этой поверхности,
пропорционален проекции градиента
скорости упорядоченного направленного
движения на эту ось
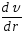 ,
площади S
и времени переноса dt:
,
площади S
и времени переноса dt:
dP
= –
 .
(2.1)
.
(2.1)
В результате между слоями возникает сила внутреннего трения, величина которой по второму закону Ньютона равна:
 ,
(2.2)
,
(2.2)
где η – коэффициент вязкости.
Для идеального газа

υТ
,
(2.3)
υТ
,
(2.3)
где ρ – плотность газа, λ – средняя длина свободного пробега молекул, υТ – средняя скорость теплового движения молекул, равная
υТ
=
 ,
(2.4)
,
(2.4)
где μ – молярная масса газа, R – универсальная газовая постоянная.
Рассмотрим газ, движущийся внутри капилляра. Выделим в нем некоторый цилиндрический объем газа радиусом r и длиной l, как показано на рис. 2.1.

Рис. 2.1
Обозначим давления на его торцах через P1 и P2. При установившемся течении сила давления на газ в цилиндре
 (2.5)
(2.5)
уравновесится силой внутреннего трения FT, которая действует вдоль боковой поверхности цилиндра со стороны окружающего его слоя газа:
 .
(2.6)
.
(2.6)
Так как площадь боковой поверхности S
= 2πrl и скорость υ(r)
уменьшается при удалении от оси трубы
(т.е.
 < 0), то из (2.2) получаем:
< 0), то из (2.2) получаем:
 .
(2.7)
.
(2.7)
С учетом (2.5) и (2.7) условие стационарности (2.6) запишется в виде:
 .
(2.8)
.
(2.8)
Разделяя переменные, получим следующее уравнение
 ,
(2.9)
,
(2.9)
интегрируя которое, получим
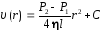 ,
(2.10)
,
(2.10)
где С – постоянная интегрирования, определяемая граничными условиями задачи.
При r=R скорость газа должна обратиться в нуль, поскольку сила внутреннего трения о стенку капилляра тормозит смежный с ней слой газа. При этом условии
 (2.11)
(2.11)
и
 .
(2.12)
.
(2.12)
Подсчитаем объемный расход газа Vt, т.е. объем газа протекающего за единицу времени через поперечное сечение трубы. Через кольцевую площадку с внутренним радиусом r и внешним r+dr за время t протекает объем газа dV = 2πr dr υ (r) t. Значит, через все сечение трубы за это время пройдет объем
V=
 (2.13)
(2.13)
и
объемный расход Vt
=
 будет равен
будет равен
 Vt
=
Vt
=
 . (2.14)
. (2.14)
Эту формулу, называемую формулой Пуазейля, можно использовать для экспериментального определения коэффициента вязкости газа.
Формула Пуазейля была получена в предположении ламинарного течения газа или жидкости. Однако с увеличением скорости потока движение становится турбулентным и слои смешиваются. При турбулентном движении скорость в каждой точке меняет свое значение и направление и сохраняется только среднее значение скорости. Критерием характера движения жидкости или газа в трубе служит число Рейнольдса:
 ,
(2.15)
,
(2.15)
где
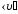 – средняя скорость потока, ρ – плотность
жидкости или газа.
– средняя скорость потока, ρ – плотность
жидкости или газа.
В гладких цилиндрических каналах переход от ламинарного течения к турбулентному происходит при Rе ≈ 1000. Поэтому в случае использования формулы Пуазейля необходимо обеспечить выполнение условия Rе < 1000. Кроме этого, эксперимент необходимо проводить таким образом, чтобы сжимаемостью газа можно было пренебречь. Это возможно тогда, когда перепад давлений вдоль капилляра значительно меньше самого давления. В используемой работе давление газа несколько больше атмосферного (103 см вод. ст.), а перепад давлений составляет ~ 10 см вод. ст., т.е. приблизительно 1 % от атмосферного.
Формула (2.14) справедлива для участка трубы, в котором установилось постоянное течение с квадратичным законом распределения скоростей (2.12) по сечению трубы. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента необходимо выполнение условия R « L ,где R – радиус, L – длина капилляра.
