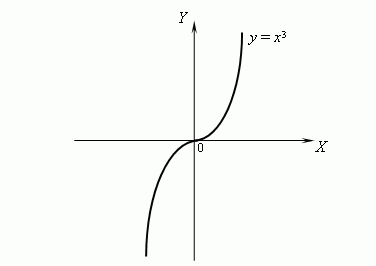Необходимое условие экстр.А

Т.

(Необходимое условие экстр.а)

Если ф-ия имеет экстр. в точке, то ее пр-иялибо равна нулю, либо не сущ-ет.

Точки, в которых пр-ия равна нулю: , называютсястационарными точками ф-ии.

Точки, в которых выполняется необходимое условие экстр.а для непрерывной ф-ии, называются критическими точками этой ф-ии. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых пр-ияне сущ-ет.

Замечание

Не в каждой своей критической точке ф-ия обязательно имеет максимум или минимум.

Первое достаточное условие экстр.А

Т.

(Первое достаточное условие экстр.а)

Пусть для ф-ии выполнены следующие условия:

1. ф-ия непрерывна в окрестности точки ;

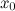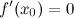2. или не сущ-ет;

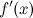3. пр-ия при переходе через точку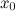меняет свой знак.

Тогда в точке ф-ияимеет экстр., причем это минимум, если при переходе через точкупр-ия меняет свой знак с минуса на плюс; максимум, если при переходе через точкупр-ия меняет свой знак с плюса на минус.

Если пр-ия при переходе через точкуне меняет знак, то экстр.а в точкенет.

Таким образом, для того чтобы исследовать функцию на экстр., необходимо:

1. найти производную ;

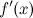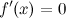2. найти критические точки, то есть такие значения , в которыхили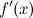не сущ-ет;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение ф-ии в экстремальных точках.

29.нап.вогн.ит.пер.ф-ииФ-ия  f ( x ) называется  выпуклой  на интервале ( a, b ), если её гр-ик на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ (a, b ).

Ф-ия  f ( x ) называется  вогнутой на интервале ( a, b ), если её гр-ик на этом интервале лежит  выше  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ (a, b ).

 

Достаточное условие вогнутости ( выпуклости ) ф-ии.

Пусть ф-ия f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x (a, b ), то ф-ия  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x (a, b ), то ф-ия  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую ф-ия меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда сл-т, что если в точке перегиба  x₀  сущ-ет вторая пр-ия  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

Рассмотрим гр-ик ф-ии  y = x3 : Эта ф-ия является вогнутой при  x > 0  и выпуклой при  x < 0. В самом деле,  y'' = 6x, но 6x > 0 при  x > 0  и  6x < 0  при  x < 0, следовательно,  y'' > 0 при x > 0 и  y'' < 0 при x < 0, откуда сл-т, что ф-ия  y = x3 является вогнутой при  x > 0 и выпуклой при x < 0. Тогда  x = 0 является точкой перегиба ф-ии  y = x3.

30.асимп.кгр.ф-ииАси́мпто́та кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность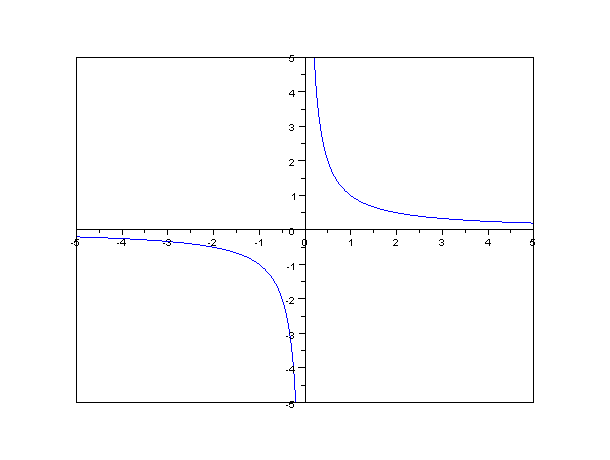Для гиперболыасимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нееВертикальная

Вертикальная асимптота — прямая вида при условии существования предела.

Как прав., при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как ф-ия ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела

.

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов

Пример наклонной асимптоты

1. 

2. 

Замечание: ф-ия может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не сущ-ет (или равен ), то наклонной асимптоты при(или) не сущ-ет.

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела , то наклонная асимптота совпадает с горизонтальной.

Горизонтальная асимптота является частным случаем наклонной при , из этого сл-т что

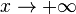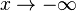1. Ф-ия не может иметь наклонную асимптоту одновременно с горизонтальной при , аналогично для, но так же возможен случай когда и вовсе нет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

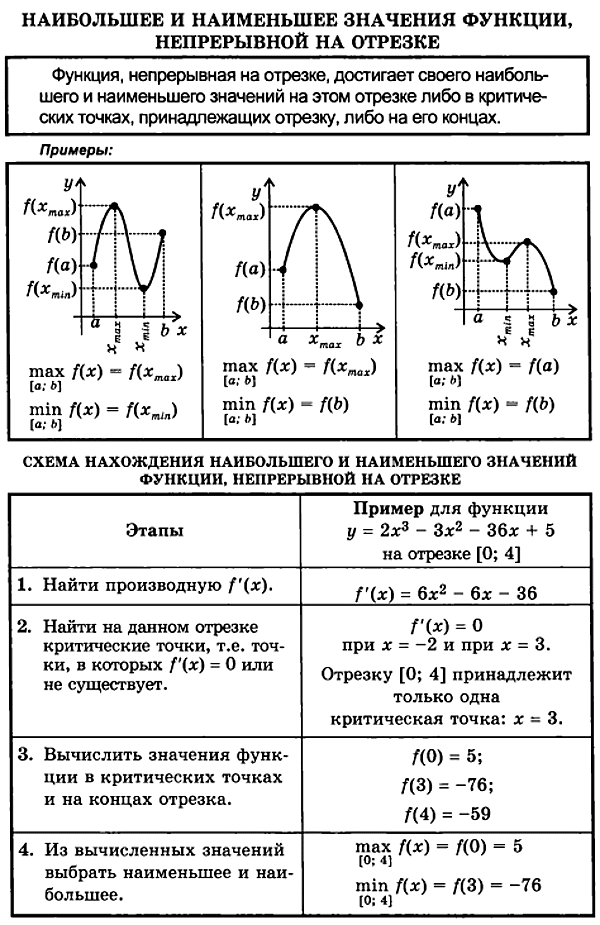
31.нах.наиб.инаим.зн.ф-ииНахождение наибольшего и наименьшего значений непрерывной ф-ии на отрезке

Говорят, что ф-ия , опрн-ая на промежуткеХ, достигает на нем своего наибольшего (наименьшего) значения, если сущ-ет точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство .

Ф-ия, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной ф-ии могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения ф-ия достигает во внутренней точке отрезка, то эта точка является точкой экстр.а.

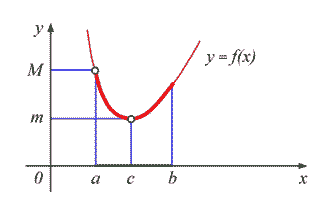
Алгоритм отыскания наибольшего и наименьшего значений непрерывной ф-ии на отрезке: найти;

найти точки, в которых илине сущ-ет, и отобрать из них те, что лежат внутри отрезка; вычислить значения ф-иив точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соотв. наибольшим и наименьшим значениями ф-иина отрезке, которые можно обозначить так:.

Если поставлена задача найти для непрерывной наф-ии, то она решается по тому же правилу, что соотв. задача для отрезка. Иногда для отыскания наибольшего или наименьшего значения непрерывной ф-иина промежуткеполезны два утверждения: если ф-ияимеет в промежуткеХ только одну точку экстр.а , причем это точка максимума, то- наибольшее значение ф-ии на промежуткеХ; если ф-ия имеет в промежуткеХ только одну точку экстр.а , причем это точка минимума, то- наименьшее значение ф-ии на промежуткеХ.

.