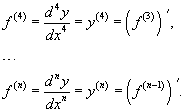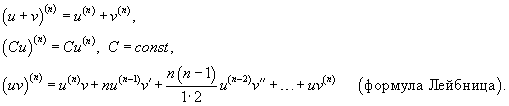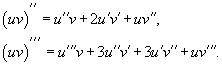1.
непр.ф-ииПусть
![]() и
и![]() .
.
Ф-ия
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если для любого
,
если для любого![]() сущ-ет
сущ-ет![]() такое, что для любого
такое, что для любого
![]()
Ф-ия
![]() непрерывна
на множестве
непрерывна
на множестве
![]() ,
если она непрерывна в каждой точке
данного множества.
,
если она непрерывна в каждой точке
данного множества.
В
этом случае говорят, что ф-ия
![]() класса
класса![]() и
пишут:
и
пишут:![]() или,
подробнее,
или,
подробнее,![]() .
.
3.
Т.
о промежуточном значении
если непрерывная ф-ия, определённая на
вещественном интервале, принимает два
значения, то она принимает и любое
значение между ними. дана непрерывная
ф-ия на отрезке
![]() Пусть
также
Пусть
также![]() и
без ограничения общности предположим,
что
и
без ограничения общности предположим,
что![]() Тогда
для любого
Тогда
для любого![]() сущ-ет
сущ-ет![]() такое,
что
такое,
что![]() .
.
4.
непр.элем.ф-ий Целая
и дробная рациональные ф-ии.
Непрерывность f(x)=const
и
f(x)=x
непосредственно
ясна. На основании теоремы о произведении
непрерывных функций вытекает непрерывность
любого одночленного выражения axm,
по теореме о сумме непрерывных функций
- непрерывность мн-чла a0xn
+
a1xn-1
+
... +an-1
+
an.
Непрерывность данных функций имеет
место на всем интервале
![]() .
Частное двух мн-члов
.
Частное двух мн-члов![]() непрерывно
всюду, кроме точекb0xm
+
b1xm-1
+...+
bm-1x
+ bm
=
0
(в этих точках - либо разрыв 2-го рода,
либо устранимый разрыв).
непрерывно
всюду, кроме точекb0xm
+
b1xm-1
+...+
bm-1x
+ bm
=
0
(в этих точках - либо разрыв 2-го рода,
либо устранимый разрыв).
Показательная
ф-ия
y=ax(a>1)
монотонно возрастает на всем интервале
![]() .
Ее значения заполняют весь интервал
.
Ее значения заполняют весь интервал![]() .
Из существования логарифма сл-т
непрерывность данной ф-ии.
.
Из существования логарифма сл-т
непрерывность данной ф-ии.
Логарифмическая
ф-ия
![]() .
Рассмотрим случайa>1.
Эта ф-ия возрастает при
.
Рассмотрим случайa>1.
Эта ф-ия возрастает при
![]() ,
и принимает любое значение из
,
и принимает любое значение из![]() .
Отсюда сл-т ее непрерывность.
.
Отсюда сл-т ее непрерывность.
Степенная
ф-ия
![]() .
При возрастанииx
от 0 до
.
При возрастанииx
от 0 до
![]() возрастает
возрастает![]() или
убывает
или
убывает![]() на
интервале
на
интервале![]() .
Следовательно, данная ф-ия непрерывна.
.
Следовательно, данная ф-ия непрерывна.
Тригонометрические
ф-ии
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Остановимся на ф-ии
.
Остановимся на ф-ии![]() .
Ее непрерывность на отрезке
.
Ее непрерывность на отрезке![]() вытекает
из ее монотонности, а также из факта
(устанавливаемого геометрически), что
при этом она принимает все значения от
-1 до 1. То же относится к любому промежутку
вытекает
из ее монотонности, а также из факта
(устанавливаемого геометрически), что
при этом она принимает все значения от
-1 до 1. То же относится к любому промежутку![]() .
Следовательно, ф-ия
.
Следовательно, ф-ия![]() непрерывна
для всех значенийx.
Аналогично - для ф-ии
непрерывна
для всех значенийx.
Аналогично - для ф-ии
![]() .
По свойствам непрерывных функций
вытекает непрерывность функций
.
По свойствам непрерывных функций
вытекает непрерывность функций![]() .
Исключение для первых двух функций -
значенияx
вида
.
Исключение для первых двух функций -
значенияx
вида
![]() ,
при которых
,
при которых![]() ,
для других двух - значения вида
,
для других двух - значения вида![]() ,
при которых
,
при которых![]() .
.
Обратные
тригонометрические ф-ии
![]() ,
,![]() ,
,![]() ,
,![]() .
Первые две непрерывны на
.
Первые две непрерывны на![]() ,
остальные - на
,
остальные - на![]()
5.
Рассмотрим функцию
![]() ,
определенную на некотором промежутке
,
определенную на некотором промежутке![]() .
Ф-ия
.
Ф-ия![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если предел ф-ии в точке
,
если предел ф-ии в точке![]() равен
значению ф-ии в этой точке,
равен
значению ф-ии в этой точке,![]() .
.
ПРИМЕР 1. Доказательство непрерывности ф-ии в точке
Односторонние пределы ф-ии в точке.
Ф-ия,
непрерывная в каждой точке промежутка
![]() ,
называетсянепрерывной
на промежутке.
Если ф-ия
,
называетсянепрерывной
на промежутке.
Если ф-ия![]() определена на промежутке
определена на промежутке![]() ,
,![]() ,
то при исследовании поведения ф-ии
,
то при исследовании поведения ф-ии![]() в окрестности точки
в окрестности точки![]() имеет
смысл говорить о пределе ф-ии в точке
имеет
смысл говорить о пределе ф-ии в точке![]() справа,
а при исследовании в окрестности точки
справа,
а при исследовании в окрестности точки![]() -
о пределе ф-ии в точке
-
о пределе ф-ии в точке![]() слева.
Число
слева.
Число![]() называетсяпределом
справа ф-ии
называетсяпределом
справа ф-ии
![]() при
при
![]() ,
стремящемся к
,
стремящемся к![]() , если для любого положительного числа
, если для любого положительного числа![]() ,
как бы мало оно ни было, сущ-ет такое
положительное число
,
как бы мало оно ни было, сущ-ет такое
положительное число![]() ,
что для всех
,
что для всех![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() ,
справедливо неравенство
,
справедливо неравенство![]() .
Говорят “предел справа ф-ии в точке
.
Говорят “предел справа ф-ии в точке![]() ”
и обозначают
”
и обозначают![]() .
Аналогично говорят “предел
слева ф-ии
.
Аналогично говорят “предел
слева ф-ии![]() в точке
в точке![]() ” и обозначают
” и обозначают
![]() ,
если для любого положительного числа
,
если для любого положительного числа![]() ,
как бы мало оно ни было, сущ-ет такое
положительное число
,
как бы мало оно ни было, сущ-ет такое
положительное число![]() ,
что для всех
,
что для всех![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() , справедливо неравенство
, справедливо неравенство![]() .
Для существования предела ф-ии в точке,
необходимо и достаточно, чтобы существовали
и совпадали односторонние пределы ф-ии
в этой точке. По той же схеме вводится
понятие непрерывности слева и непрерывности
справа. Ф-ия
.
Для существования предела ф-ии в точке,
необходимо и достаточно, чтобы существовали
и совпадали односторонние пределы ф-ии
в этой точке. По той же схеме вводится
понятие непрерывности слева и непрерывности
справа. Ф-ия![]() ,
опрн-ая на отрезке
,
опрн-ая на отрезке![]() ,
,![]() ,
непрерывна справа в точке
,
непрерывна справа в точке![]() ,
если
,
если![]() и непрерывна слева в точке
и непрерывна слева в точке![]() ,
если
,
если![]() .
Для того чтобы ф-ия была непрерывна в
точке
.
Для того чтобы ф-ия была непрерывна в
точке![]() необходимо
и достаточно, чтобы односторонние
пределы ф-ии в точке совпадали со
значением ф-ии в этой точке:
необходимо
и достаточно, чтобы односторонние
пределы ф-ии в точке совпадали со
значением ф-ии в этой точке:![]() .
Если хотя бы одно из равенств нарушается,
говорят о разрыве в точке
.
Если хотя бы одно из равенств нарушается,
говорят о разрыве в точке![]() .
.
ПРИМЕР 2. Вычисление односторонних пределов
Классификация разрывов.
Если
хотя бы одно из равенств
![]() нарушается,
говорят о разрыве в точке
нарушается,
говорят о разрыве в точке![]() .
Если
.
Если![]() и
односторонние пределы конечны, то разрыв
в точке
и
односторонние пределы конечны, то разрыв
в точке![]() называетсяустранимым.
Если
называетсяустранимым.
Если
![]() и
оба односторонние пределы конечны, то
говорят оскачке
ф-ии в точке
и
оба односторонние пределы конечны, то
говорят оскачке
ф-ии в точке
![]() .
Устранимый разрыв и скачок называютсяразрывами
первого рода.
Если один из односторонних пределов
бесконечен или не сущ-ет, то разрыв
называется разрывом
второго рода.
Так же, как для предела и непрерывности,
говорят о разрыве слева и разрыве справа.
.
Устранимый разрыв и скачок называютсяразрывами
первого рода.
Если один из односторонних пределов
бесконечен или не сущ-ет, то разрыв
называется разрывом
второго рода.
Так же, как для предела и непрерывности,
говорят о разрыве слева и разрыве справа.
6.откр.изамк.мн. Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М С помощью кванторов определение запишется следующим образом: М ∈ Ε — открытое, если ∀ у∈М ∃ ε>0 : Uε(y) < M
Простым языком — открытое множество состоит из внутренних точек. Примерами открытого множества являются пустое множество, прямая, интервал (а, b)
Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения. Теперь с помощью кванторов: х*∈ E — граничная точка, если ∀Uε(x) ∩ М ≠ ∅ и ∀Uε(x) ∩ Е\М
Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отр. [a, b]
Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).
Докажем несколько теорем, связанных с открытым и замкнутым множествами.
Т. 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством. Доказательство: Обозначим дополнение множества А как множество В: В = Е\А Доказывать будем от противного. Предположим, что В — незамкнутое. Тогда сущ-ет граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д. В кванторах доказательство можно записать короче: Предположим, что В — незамкнутое, тогда: (1) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ∩ В ≠ ∅ (определение граничной точки) (2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ А ≠ ∅ (определение открытоко множества) Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.
Т. 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством. Доказательство: Обозначим дополнение множества А как множество В: В = Е\А Доказывать будем от противного. Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д. В кванторах это выглядеть будет следующим образом: Предположим, что В — замкнутое, тогда: (1) ∀ х∈А*:х∈A (из условия) (1) ∀ х∈А*:х∈В (из предположения) Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.
Т. 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅ Доказательство: Начнём записывать подробно, но сразу использую кванторы. Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е. (1) ∃ х∈А*:х∈С ⇒ ∀Uε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С) (2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ В (определение открытого множества С) Из (1) и (2) сл-т, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.


8.пон.пр.г.и.м.см.пр.
Средней
скоростью изменения ф-ии
![]() при
переходе независимой переменной от
значения
при
переходе независимой переменной от
значения![]() к
значению
к
значению![]() называется
отношение приращения
называется
отношение приращения![]() ф-ии
к приращению
ф-ии
к приращению![]() независимой
переменной, то есть
независимой
переменной, то есть
![]()
Истинной
или мгновенной
скоростью изменения ф-ии
![]() при
заданном значении независимой переменной
при
заданном значении независимой переменной![]() называется
предел, к которому стремится средняя
скорость изменения ф-ии при стремлению
к нулю приращения аргумента
называется
предел, к которому стремится средняя
скорость изменения ф-ии при стремлению
к нулю приращения аргумента![]() :
:
![]()
(Механический смысл производной)
Пусть
задан путь
![]() движения
материальной точки. Скорость данной
материальной точки в момент времени
движения
материальной точки. Скорость данной
материальной точки в момент времени![]() есть
пр-ия от пути
есть
пр-ия от пути![]() по
времени
по
времени![]() :
:
![]()
Пр-ия
ф-ии
![]() ,
вычисленная при заданном значении
,
вычисленная при заданном значении![]() ,
равна тангенсу угла, образованного
положительным направлением оси
,
равна тангенсу угла, образованного
положительным направлением оси![]() и
положительным направлением касательной,
проведенной к гр-ику этой ф-ии в точке
с абсциссой
и
положительным направлением касательной,
проведенной к гр-ику этой ф-ии в точке
с абсциссой![]() :
:
![]()
0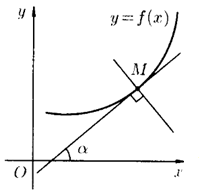
9.Выв.табл.произв.ст.,пок,лог.ф-ий![]()
![]()
![]()
![]()
![]()
![]()
10.8дл.триг.ф-ий
Производные тригонометрических и обратных тригонометрических функций
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11.фор.д.пол.прир.ф.,пр.с,р,пО:
Полным приращением ф-ии z =![]() (х,
у) называется разность
(х,
у) называется разность![]()
Замечание.
В общем случае![]() Пусть,
например,
Пусть,
например,
![]()
Аналогично
полное приращение ф-ии![]()
![]()
Пр-ия суммы (разности) функций
Пр-ия алгебраической суммы функций выражается следующей теоремой.
Пр-ия суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
![]()
Пр-ия конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
![]()
Пр-ия произведения функций.
Пусть u(x) и u(x) - дифференцируемые ф-ии. Тогда произведение функций u(x)v(x) также дифференцируемо и
![]()
Пр-ия произведения двух функций не равана произведению производных этих функций.
Пр-ия частного функций.
Пусть u(x) и u(x) - дифференцируемые ф-ии. Тогда, если v(x) ≠ 0, то пр-ия частного этих функций вычисляется по формуле
![]()
12.ос.пр.выч.пр. 1. Константу можно выносить за знак производной.
![]()
![]() 2.
Пр-ия
суммы/разности.
2.
Пр-ия
суммы/разности.
Пр-ия суммы/разности двух функций равна сумме/разности производных от каждой из функций.
![]()
Пример
![]()
Больше примеров решений →
3. Пр-ия произведения.
![]()
Пример
![]()
Больше примеров решений →
4. Пр-ия частного.
![]()
Пример
![]()
Больше примеров решений →
5. Пр-ия сложной ф-ии.
Пр-ия
сложной ф-ии равна производной этой
ф-ии по промежуточному аргументу
![]() ,
умноженной на производную от промежуточного
аргумента
,
умноженной на производную от промежуточного
аргумента![]() по
основному аргументу
по
основному аргументу![]() .
.
![]() и
и
![]() имеют
производные соотв. в точках
имеют
производные соотв. в точках![]() и
и![]() .
Тогда
.
Тогда
![]()
Т.
(О производной обратной ф-ии)
Если
ф-ия
![]() непрерывна
и строго монотонна в некоторой окрестности
точки
непрерывна
и строго монотонна в некоторой окрестности
точки![]() и
дифференцируема в этой точке, то обратная
ф-ия
и
дифференцируема в этой точке, то обратная
ф-ия![]() имеет
производную в точке
имеет
производную в точке![]() ,
причем
,
причем![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
13св.меж.сущ.пр.икас.
По аналогии с односторонними пределами
вводится понятия левой и правой
производных. Если ф-ция y=f(x) непрерывна
слева в точке
![]() и
сущ-ет предел
и
сущ-ет предел![]() ,
где
,
где![]() ,
то этот предел называютлевой
производной
ф-ции f в точке
,
то этот предел называютлевой
производной
ф-ции f в точке
![]() и
обозначают
и
обозначают![]()
![]() .
Аналогично, если ф-ция y=f(x) непрерывна
справа в точке
.
Аналогично, если ф-ция y=f(x) непрерывна
справа в точке![]() ,
то предел
,
то предел![]() называютправой
производной
ф-ции f в точке
называютправой
производной
ф-ции f в точке
![]() и
обозначают
и
обозначают![]()
![]() .
.
Прямые,
проходящие через точку
![]() с
угловыми коэффициентами
с
угловыми коэффициентами![]()
![]() и
и![]()
![]() называют
соотв.левой
и
правой касательными
к гр-ику ф-ции y=f(x) в точке
называют
соотв.левой
и
правой касательными
к гр-ику ф-ции y=f(x) в точке
![]() .
Из существования производной
.
Из существования производной![]() сл-т
существование
сл-т
существование![]()
![]() и
и![]()
![]() и
рав-во:
и
рав-во:![]()
![]() =
=![]()
![]() =
=![]() .
В этом случае правая и левая касательные
к гр-ику ф-ции y=f(x) в точке
.
В этом случае правая и левая касательные
к гр-ику ф-ции y=f(x) в точке![]() совпадают
с касательной в точке
совпадают
с касательной в точке![]() .Обратное
утверждение также верно.
.Обратное
утверждение также верно.
Если
![]() то
говорят, что ф-ция y=f(x) имеет в точке
то
говорят, что ф-ция y=f(x) имеет в точке![]() производную,
равную
производную,
равную![]() и
пишут
и
пишут![]() .
Аналогично, если
.
Аналогично, если![]() ,
то
,
то![]() .
.
В
случае, когда
![]() или
или![]() говорят,
что ф-ция y=f(x) имеет в точке
говорят,
что ф-ция y=f(x) имеет в точке![]() бесконечную
производную.
(иногда добавляют : определенного знака).
бесконечную
производную.
(иногда добавляют : определенного знака).
ОДНОСТОРОННЯЯ КАСАТЕЛЬНАЯ к гр-ику ф-ии y=f(х) в точке М0 — правая (или левая) касательная, т. е. предельное положение секущего луча М0М, когда точка М стремится к М0, оставаясь справа (соотв. слева) от точки М0. На рис. 178 М0N — правая и М0Р — левая касательные.
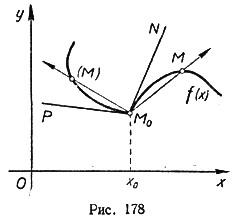
14.диф.ф-ии,пон.диф,геом.см.12.Дифференци́руемая
(в точке) фу́нкция —
это ф-ия, у которой сущ-ет дифф-ал (в
данной точке). Дифференцируемая на
некотором множестве
ф-ия — это ф-ия, дифференцируемая в
каждой точке данного множества Ф-ия
![]() одной
переменной является дифференцируемой
в точке
одной
переменной является дифференцируемой
в точке![]() своей
области определения
своей
области определения![]() ,
если сущ-ет такая константа
,
если сущ-ет такая константа![]() ,
что для любой точки
,
что для любой точки![]() верно
верно
|
|
при
этом число
![]() неизбежно
равно производной
неизбежно
равно производной
|
|
Ф-ия
![]() переменных
переменных![]() является
дифференцируемой в точке
является
дифференцируемой в точке![]() своей
области определения
своей
области определения![]() ,
если для любой точки
,
если для любой точки![]() существуют
такие константы
существуют
такие константы![]() ,
что
,
что
|
|
где
![]() .
.
В
этой записи ф-ия![]()
|
|
является
дифф-алом ф-ии
![]() в
точке
в
точке![]() ,
а числа
,
а числа![]() являютсячастными
производными
ф-ии
являютсячастными
производными
ф-ии
![]() в
точке
в
точке![]() ,
то есть
,
то есть
|
|
где
![]() —
вектор, все компоненты которого, кроме
—
вектор, все компоненты которого, кроме![]() -ой,
равны нулю, а
-ой,
равны нулю, а![]() -ая
компонента равна 1.
-ая
компонента равна 1.
Знак дифф-ала используется в выражении для интеграла
 .
При этом иногда (и не вполне корректно)
дифф-ал
.
При этом иногда (и не вполне корректно)
дифф-ал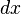 вводится
как часть определения интеграла.
вводится
как часть определения интеграла.Также знак дифф-ала используется в обозначении Лейбница для производной
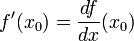 .
Это обозначение мотивировано тем, что
для дифф-алов ф-ии
.
Это обозначение мотивировано тем, что
для дифф-алов ф-ии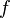 и
тождественной ф-ии
и
тождественной ф-ии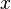 верно
соотношение
верно
соотношение
![]()
Геометрический смысл дифф-ала
На
гр-ике ф-ии
![]() возьмем произвольную точку
возьмем произвольную точку![]() и дадим аргументу
и дадим аргументу![]() приращение
приращение
![]() .
При этом ф-ия получит приращение
.
При этом ф-ия получит приращение![]() (на
рисунке отр.
(на
рисунке отр.![]() ).
).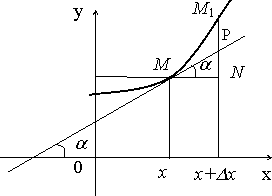
Проведем
касательную к кривой
![]() в точке
в точке![]() и обозначим угол ее наклона к оси
и обозначим угол ее наклона к оси![]() через
через![]() ,
тогда
,
тогда![]() .
Из треугольника
.
Из треугольника![]() находим
находим![]()
![]() ,
т.е.
,
т.е.![]() .
.
Таким
образом, дифф-ал
ф-ии численно равен приращению ординаты
касательной, проведенной к гр-ику ф-ии
![]() в данной точке, когда аргумент
в данной точке, когда аргумент![]() получает приращение
получает приращение![]() .
.
15.осн.ф.выч.дифф. 1. Константу можно выносить за знак дифф-ала.
![]()
2. Дифф-ал суммы/разности.
Дифф-ал суммы/разности функций равен суме/разности дифф-алов от каждого из слагаемых.
![]()
3. Дифф-ал произведения.
![]()
4. Дифф-ал частного.
![]()
5. Дифф-ал константы равен нулю.

17.
|
Производные высшего порядка |
|
|
|
Пусть y = f(x) является дифференцируемой функцией. Тогда пр-ия также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную ф-ии f, которая обозначается в виде
Аналогично, если f '' сущ-ет и дифференцируема, мы можем вычислить третью производную ф-ии f:
Производные более высокого порядка (если они существуют), определяются как
Для нахождения производных высшего порядка можно использовать следующие формулы:
В частности, для производной второго и третьего порядка формула Лейбница принимает вид
|
Производные n-го порядка от основных элементарных функций
Справедливы формулы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Формула Лейбница
Если u и v - n-кратно дифференцируемые ф-ии, то
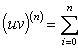
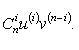
17.пр.выс.пор.
– см.пред. Формула Лейбница
для
![]() -ой
производной произведения двух функций —
обобщение правиладифференцирования
произведения (и отношения) двух функций
на случай
-ой
производной произведения двух функций —
обобщение правиладифференцирования
произведения (и отношения) двух функций
на случай
![]() -кратного
дифференцирования.
-кратного
дифференцирования.
Пусть
ф-ии
![]() и
и![]() —
—![]() раз
дифференцируемые ф-ии, тогда
раз
дифференцируемые ф-ии, тогда
![]() где
где
![]() —биномиальные
коэффициенты.
—биномиальные
коэффициенты.
Доказательство формулы осуществляется по индукции с использованием правила произведения. В мультииндексной записи формула может быть записана в более общем виде:
![]()
Эта
формула может быть использована для
получения выражения для композиции
дифф-альных операторов. В самом деле,
пусть P
и Q —
дифф-альные операторы (с коэффициентами,
которые дифференцируемы достаточное
число раз) и
![]() .
ЕслиR
также является дифф-альным оператором,
то справедливо равенство:
.
ЕслиR
также является дифф-альным оператором,
то справедливо равенство:
![]()
Непосредственное вычисление дает:
![]()
18.дифф.выс.пор.,отс.вар-тиДля
ф-ии, зависящей от одной переменной
![]() второй и третий дифф-алы выглядят так:
второй и третий дифф-алы выглядят так:
![]()
![]()
Отсюда
можно вывести общий вид дифф-ала n-го
порядка от ф-ии
![]() :
:
![]()
При
вычислении дифф-алов высших порядков
очень важно, что
![]() есть
произвольное и не зависящее от
есть
произвольное и не зависящее от![]() ,
которое при дифференцировании по
,
которое при дифференцировании по![]() сл-т рассматривать как постоянный
множитель.
сл-т рассматривать как постоянный
множитель.
Дифф-ал высшего порядка ф-ии нескольких переменных
Если
ф-ия
![]() имеет непрерывные частные производные
второго порядка, то дифф-ал второго
порядка определяется так:
имеет непрерывные частные производные
второго порядка, то дифф-ал второго
порядка определяется так:![]() .
.
![]()
![]()
![]()
![]()
Символически
общий вид дифф-ала n-го
порядка от ф-ии
![]() выглядит
следующим образом:
выглядит
следующим образом:
![]()
где
![]() ,
а
,
а![]() произвольные
приращения независимых переменных
произвольные
приращения независимых переменных![]() .
Приращения
.
Приращения![]() рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифф-ала к следующему. Сложность
выражения дифф-ала возрастает с
увеличением числа переменных.
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифф-ала к следующему. Сложность
выражения дифф-ала возрастает с
увеличением числа переменных.
Неинвариантность дифф-алов высшего порядка
При
![]() ,
,![]() -й
дифф-ал не инвариантен (в отличие
от инвариантности первого дифф-ала),
то есть выражение
-й
дифф-ал не инвариантен (в отличие
от инвариантности первого дифф-ала),
то есть выражение![]() зависит,
вообще говоря, от того, рассматривается
ли переменная
зависит,
вообще говоря, от того, рассматривается
ли переменная![]() как
независимая, либо как некоторая
промежуточная ф-ия другого переменного,
например,
как
независимая, либо как некоторая
промежуточная ф-ия другого переменного,
например,![]() .
.
Для
доказательства неинвариантности
дифф-алов высшего порядка достаточно
привести пример.
При n
= 2 и ![]() :
:
если
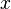 —
независимая переменная, то
—
независимая переменная, то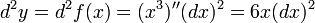
если
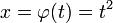 и
и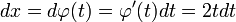
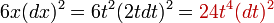
при этом,
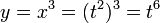 и
и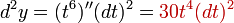
С
учётом зависимости
![]() ,
уже второй дифф-ал не обладает свойством
инвариантности при замене переменной.
Также не инвариантны дифф-алы порядков
3 и выше.
,
уже второй дифф-ал не обладает свойством
инвариантности при замене переменной.
Также не инвариантны дифф-алы порядков
3 и выше.
19.т.фермаДля
любого натурального
числа
![]() урав.
урав.
![]()
не
имеет решений в целых ненулевых числах
![]() .
.
20.т.ролляЕсли
вещественная ф-ия, непрерывная на отрезке
![]() и
дифференцируемая на интервале
и
дифференцируемая на интервале![]() ,
принимает на концах этого интервала
одинаковые значения, то на этом интервале
найдётся хотя бы одна точка, в которой
пр-ия ф-ии равна нулю. Если ф-ия на отрезке
постоянна, то утверждение очевидно,
поскольку пр-ия ф-ии равна нулю в любой
точке интервала.
,
принимает на концах этого интервала
одинаковые значения, то на этом интервале
найдётся хотя бы одна точка, в которой
пр-ия ф-ии равна нулю. Если ф-ия на отрезке
постоянна, то утверждение очевидно,
поскольку пр-ия ф-ии равна нулю в любой
точке интервала.
Если же нет, поскольку значения ф-ии в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстр., и по лемме Ферма, в этой точке пр-ия равна 0.
21.т.лагранжа
Пусть
группа G конечна и H — её подгруппа. Тогда
порядок G равен порядку H, умноженному
на количество её левых или правых классов
смежности (индекс). Количество
правых и левых смежных классов любой
подгруппы
![]() в
в![]() одинаково
и называетсяиндексом
подгруппы
одинаково
и называетсяиндексом
подгруппы
![]() в
в![]() (обозначается
(обозначается![]() ).
).
Количество
правых и левых смежных классов любой
подгруппы
![]() в
в![]() одинаково
и называетсяиндексом
подгруппы
одинаково
и называетсяиндексом
подгруппы
![]() в
в![]() (обозначается
(обозначается![]() ).
).
Порядок
любой подгруппы конечной группы
![]() делит
порядок
делит
порядок![]() .
.
Из
того, что порядок
элемента
группы равен порядку циклической
подгруппы, образованной этим элементом,
сл-т, что порядок любого элемента конечной
группы
![]() делит
порядок
делит
порядок![]() .
Это следствие обобщаеттеорему
Эйлера
и малую
теорему Ферма
в теории
чисел.
.
Это следствие обобщаеттеорему
Эйлера
и малую
теорему Ферма
в теории
чисел.
Группа
порядка
![]() ,
где
,
где![]() —простое
число,
циклична. (Поскольку порядок элемента,
отличного от единицы, не может быть
равен 1, все элементы, кроме единицы,
имеют порядок
—простое
число,
циклична. (Поскольку порядок элемента,
отличного от единицы, не может быть
равен 1, все элементы, кроме единицы,
имеют порядок
![]() ,
и значит, каждый из них порождает группу.)
,
и значит, каждый из них порождает группу.)
23.т.лопиталя
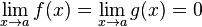 либо
либо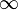 ;
;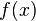 и
и
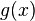 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности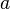 ;
;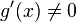 в
проколотой окрестности
в
проколотой окрестности
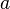 ;
;сущ-ет
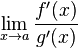 ,
,
тогда
сущ-ет
![]() .
.
Пределы также могут быть односторонними.
Отношение бесконечно малых
Докажем
теорему для случая, когда пределы функций
равны нулю (то есть неопределённость
вида
![]() ).
).
Поскольку
мы рассматриваем ф-ии
![]() и
и![]() только
в правой проколотой полуокрестности
точки
только
в правой проколотой полуокрестности
точки![]() ,
мы можем непрерывным образом их
доопределить в этой точке: пусть
,
мы можем непрерывным образом их
доопределить в этой точке: пусть![]() .
Возьмём некоторый
.
Возьмём некоторый![]() из
рассматриваемой полуокрестности и
применим к отрезку
из
рассматриваемой полуокрестности и
применим к отрезку![]() теорему
Коши. По этой теореме получим:
теорему
Коши. По этой теореме получим:
![]() ,
,
но
![]() ,
поэтому
,
поэтому![]() .
.
Дальше,
записав определение предела отношения
производных и обозначив последний через
![]() ,
из полученного равенства выводим:
,
из полученного равенства выводим:
![]() для
конечного предела и
для
конечного предела и
![]() для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.