§14. Линии второго порядка

1°. Определение эллипса, каноническое уравнение эллипса, исследование формы эллипса.

Определение 1. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек и этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.

Составим уравнение эллипса. Выберем на плоскости декартову прямоугольную систему координат так, чтобы ось проходила через фокусы и , и имела одинаковое направление с вектором , а начало координат было в середине отрезка . Пусть . Тогда – координаты фокуса а – координаты фокуса (рис.1).

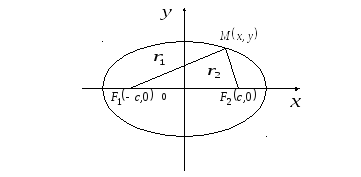
Рис. 1

Пусть – произвольная точка эллипса. Отрезки и называются фокальными радиусами точки . Положим , Тогда

, . (1)

Согласно определению эллипса, точка принадлежит эллипсу тогда и только тогда, когда для некоторого числа , большего , выполняется равенство

. (2)

Уравнение (2) является уравнением эллипса в выбранной декартовой прямоугольной системе координат.

Представим уравнение (2) в виде

и возведём обе части в квадрат. Получим

,

откуда

.

Вновь доведём обе части этого равенства в квадрат:

,

откуда

, (3)

причём .

Положим , тогда из (5) следует

. (4)

Таким образом, координаты любой точки эллипса удовлетворяют уравнению (4). Покажем теперь, что верно и обратное утверждение: любая точка , координаты которой удовлетворяют уравнению , есть точка эллипса. Для этого убедимся, что . Подставив значение из (4) в правую часть выражений (1), получим

,

откуда

, .

Так как из уравнения (4) следует , т.е. , , то , а это значит, что . Следовательно,

, . (5)

Отсюда получаем , а это значит, что точка принадлежит эллипсу.

Уравнение (4) называется каноническим уравнением эллипса. Числа и называются соответственно большой и малой полуосями эллипса.

Исследуем форму эллипса. Из канонического уравнения эллипса (4) следует, что , . Это означает, что эллипс расположен в прямоугольнике, образованном прямыми , , и, следовательно, является ограниченной кривой.

Так как каноническое уравнение эллипса содержит только квадраты текущих координат, то из принадлежности точки эллипсу следует, что и точки , , также лежат на эллипсе. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии.

Рис. 2

Если в уравнении (4) положим , то получим или . Значит, , – точки пересечения эллипса с осью .

Полагая , получаем , т.е. точками пересечения эллипса с осью являются , . Точки , называются вершинами эллипса.

В силу симметрии достаточно исследовать форму эллипса только в первой четверти. Для первой четверти из уравнения (6) получим

.

Функция определена и непрерывна при , поэтому график функции асимптот не имеет. Вычислим производные

и найдём, что при производные . Следовательно, данная функция монотонно убывает и выпукла вверх. График функции в первой четверти изображён на рис. 2. Эллипс строим с учётом симметрии (см. рис. 1).

Определение 2. Число

(6)

называется эксцентриситетом эллипса.

Так как , то . Перепишем формулу (6) для эксцентриситета в виде

.

Отсюда видно, что характеризует форму эллипса: если , то , а эллипс становится похожим на окружность. При увеличении эллипс становится более вытянутым.

Пусть – произвольная точка эллипса. Её фокальные радиусы и задаются формулами (5), которые в силу (6) имеют вид

, . (7)

Восстановим в одном из фокусов эллипса перпендикуляр к оси до пересечения в точке с эллипсом. Фокальным параметром эллипса называется длина отрезка .

Так как точка имеет координаты , то

,

откуда , т.е. .

Выведем параметрическое уравнение эллипса. Перейдём в каноническом уравнении эллипса (4) к переменным

.

Получим уравнение окружности . Параметрическое уравнение этой окружности, как известно, имеет вид . Тогда

.

Полученные уравнения являются параметрическими уравнениями эллипса.