1.7 Закон больших чисел. Предельные теоремы

Теорема Чебышева. Если Х – неотрицательная случайная величина и М(Х) – её математическое ожидание, то для любой А>0 имеет место неравенство

, (1.7.1)

или . (1.7.1’)

Если случайная величина имеет дисперсию D(X), то для любого имеет место неравенство Чебышева:

, (1.7.2)

или . (1.7.2’)

Если 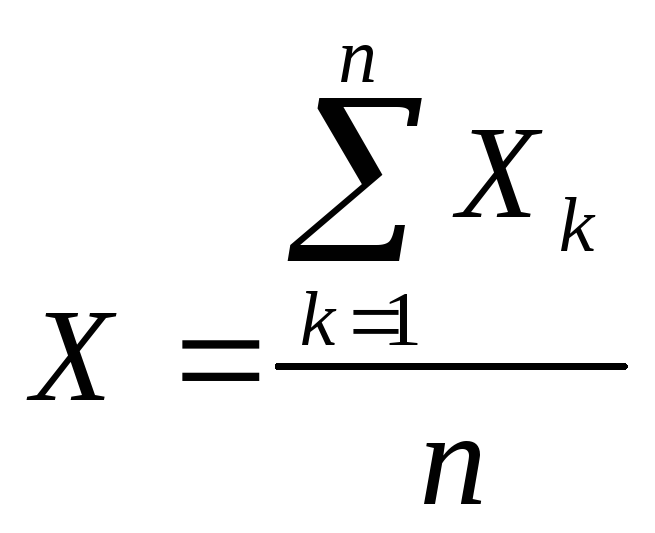- средняя арифметическая независимых случайных величин,k=1, … n, каждая из которых имеет и, то неравенство Чебышева принимает вид

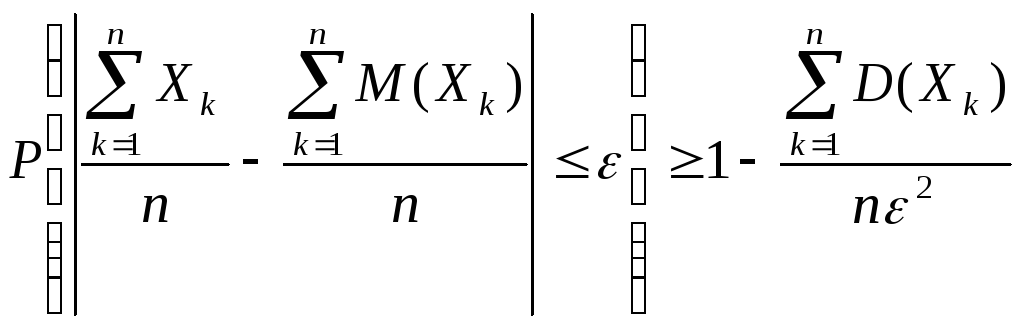. (1.7.3)

Для случайных величин, одинаково распределённых с и, неравенство (1.7.3) принимает вид

. (1.7.4)

Если дисперсия независимых случайных величин равномерно ограничены числом С, то следствием (1.7.2) является неравенство

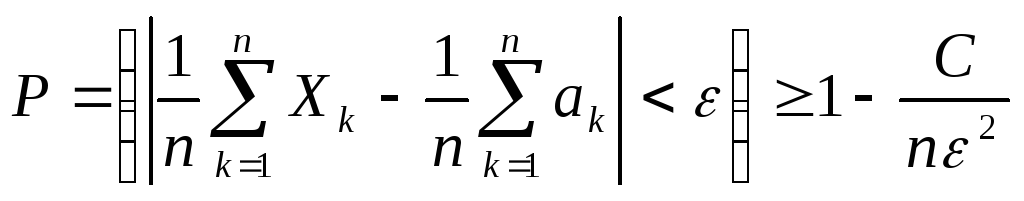. (1.7.5)

Следствием (1.7.2) является также неравенство Чебышева для случайной величины, распределенной по биноминальному закону:

, (1.7.6)

и для случайной величины, равной частности появлений события в n независимых испытаниях:

. (1.7.7)

Теорема Ляпунова. Пусть дана последовательность независимых случайных величин ,k=1, … n,…, для каждой из которых существует математическое ожидание =, дисперсия=и третий центральный абсолютный момент. Если выполняется условие

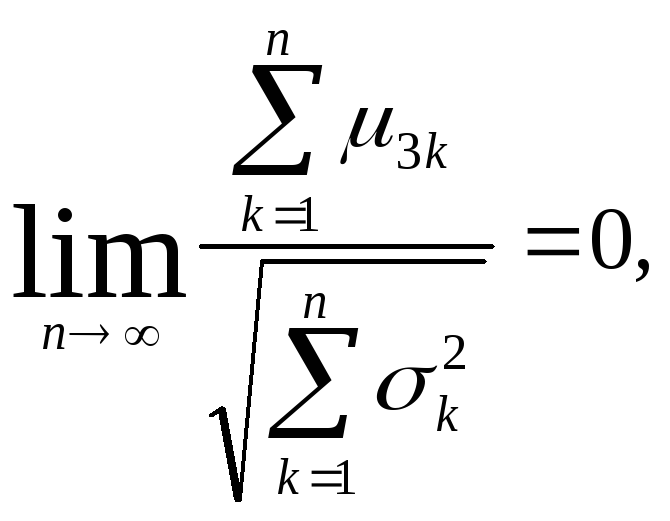(1.7.8)

то случайная величина распределена нормально с математическим ожиданиемМ(Х)=∑ и дисперсией=.

Теорема Ляпунова относится к группе теорем, объединённых общим названием центральная предельная теорема. Одна из простых формулировок центральной предельной теоремы относится к одинаково распределённым случайным величинам: если - независимые одинаково распределённые случайные величины с математическими ожиданиямии дисперсиями, то при неограниченном увеличении их числаn закон распределения их суммы X приближается к нормальному с параметрами M(X)=na и D(X)= .

Теорема Лапласа. Пусть m – частота появлений события A в n независимых испытаниях, а p – вероятность наступления события A в отдельном испытании. При случайная величинараспределена нормально сМ(Х)=0 и D(X)=1, то есть

.

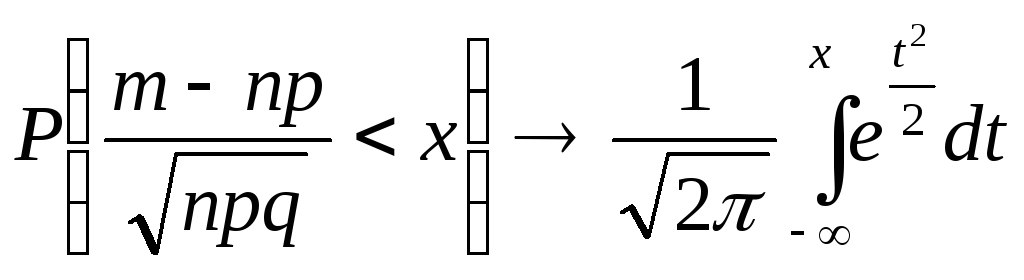Приближение формулы Муавра – Лапласа следует из того, что закон распределения случайной величины при большомn близок к нормальному с плотностью вероятности .

Задача 1.7.1

Математическое ожидание скорости ветра на аэродроме равно 7 м/с. Оценить вероятность того, что скорость ветра на аэродроме а) не превзойдет 28 м/с : б) будет не менее 35 м/с.

Решение. Случайная величинаХ– скорость ветра. а) по условиюА– 28 м/с. Применяем неравенство (1.7.1’):

б) По условию А= 35 м/с. Применяем неравенство (1.7.1):

.

Задача 1.7.2

Средний вес детали равен 50 г, а дисперсия равна 0,1. Оценить вероятность того, что вес случайно выбранной из партии детали окажется в границах (49,5;50,5).

Решение. Случайная величинаХ– вес детали. По условию

=50 г,=0,1 и=0,5. Неравенство 49,5<X<50,5 равносильно -0,5<X-50<0,5 , или. Поэтому применяем неравенство Чебышева (1.7.2’):

Искомая вероятность не меньше 0,6.

Задача 1.7.3

Сумма всех вкладов в некоторую сберегательную кассу составляет 20000 руб., а вероятность того, что случайно взятый вклад не превышает 100 руб., равна 0,8. Что можно сказать о числе вкладчиков данной сберкассы?

Решение. ПустьХ – размер случайно взятого вклада ,аn– число всех вкладов. Тогда из условия задачи средний размер вкладаТак каки по неравенству (1.7.1’)тоОтсюдаи, следовательно,

Задача 1.7.4

Ёмкость изготовляемого заводом конденсатора должна быть по техническим условиям равной 2 мкФ с разрешённым допуском 0,1 мкФ. Завод добился средней ёмкости, равной 2 мкФ с дисперсией, равной 0,004 мкФ. Какова вероятность изготовления бракованного конденсатора? Расчёт провести по неравенству Чебышева, предположив, что ёмкости конденсаторов распределены по нормальному закону с теми же параметрами.

Решение. Конденсатор будет бракованным, если отклонение ёмкости конденсатора Х от среднего значения М(Х)=2 мкФ будет по абсолютной величине болеем =0,1 мкФ. По неравенству Чебышева (1.7.2 ) имеем

а поэтому вероятность события P

Если же предположить, что значения ёмкости распределены по нормальному закону, то

Видим, что, используя значение о нормальном законе распределения, ответ получаем более точным. Неравенство же Чебышева дает грубую оценку, зато оно применимо к случайным величинам, распределенным по любому закону.