1.6 Функция распределения случайной величины. Непрерывная случайная величина
Функция распределения F(x) примет значение
F(x)=P(X<x). (1.6.1)
Свойства
функции распределения: F(-
)
=0;
F(+
)
= 1. О < F(x)
< 1;
если х2
>
,
to
F(
)
F(
).
Вероятность попадания случайной величины X в промежуток [а;b) определяется формулой
P(a<X<b) = F(b)-F{a). (1.6.2)
Существуют случайные величины, множество значений которых непрерывно заполняют некоторый числовой промежуток.
Если функция F(x) распределения случайной величины X непрерывна и имеет почти всюду (кроме, возможно, конечного числа точек) непрерывную производную, то случайную величину X называют непрерывной, а функцию f(x) = F'(x) называют плотностью вероятности случайной величины X.Имеют место формулы:
а)
б)
в)
;
г)
.(1.6.3)
Вероятность того, что непрерывная случайная величина имеет конкретное значение, равна нулю.
Математическим ожиданием непрерывной случайной величины X называется числоM(X), равное
(1.6.4)
Дисперсия D(x)непрерывной случайной величины Xопределяется по формуле
(1.6.5)
Задача 1.6.1
Прибор состоит из двух блоков,
вероятность безотказной работы каждого
из которых в течение времени
равна 0,5. Найти рядраспределения
для числа блоков, работающих, и момент
t=T
. Найти
функцию распределения F(x)
ДСВ
X
Решение.
Обозначим
состояние каждого блока через (R)
или
(О),
в
зависимости
от того, работает он или отказал.
Вероятность F(R)=P(O)=1/2.
Множество всех
исходов опыта Е
содержит
4 элемента, вероятность каждого равна
¼,
Е = {(0,0); (0,R);
(R,0);
(R,R)}-
Случайная
величина X-
число
работающих блоков к моменту t.
Случаю
(О
О) соответствует
значение X=0
(оба
блока отказали),
= Р(Х
= 0) = 1/4,
случаям (О R)
и (R
О) соответствует
значение Х=1 (один
блок отказал),
=Р(X
= 1)=1/4+1/4=1/2. Случаю
(R
R)
соответствует
значение
Х=2
(оба
блока работают) ,
=Р(Х
=
2) =1/4.
Ряд распределения для случайной величины Х- числа работающих блоков имеет вид
|
|
0 |
1 |
2 |
|
|
1/4 |
1/2 |
1/4 |
Если x
0,
то F(x)=0,
так
как нет ни одного значения X
левее
нуля.
Если 0
< x
1
,то в промежуток (-
;0) попадает одно значениеХ=0,
следовательно,F(x)=P(x=0)=1/4.
Если 1
< x
2 ,то
в промежуток (-
;х) попадает два значения X
=0
и X=1,
следовательно,
F(x)
= Р(Х = 0)
+ Р(Х
= 1)
= ¾.
Если 2
< x
,то в промежуток (-
;x)
попадают
все значения X,
т.е.
Х=0,
Х=1, Х=2. Следовательно,
F(x)=1.
Получаем
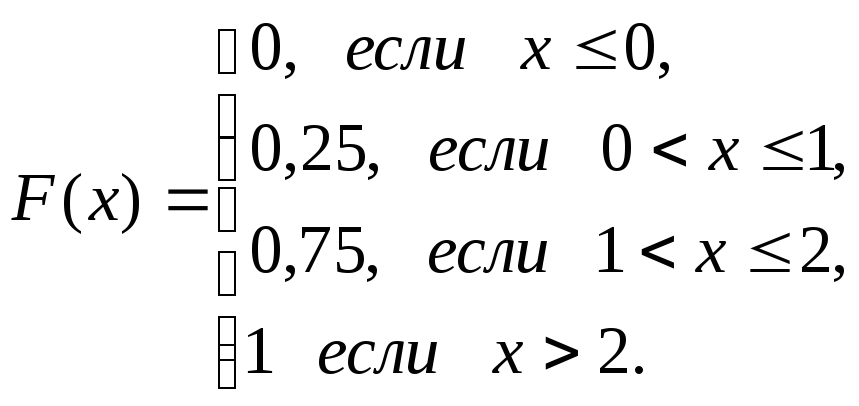
Задача 1.6.2
Составить функцию распределения случайной величины, распределенной по биномиальному закону.
Решение.
X
принимает
значение
с
вероятностями.
При
.
При
нужно
найти сумму значений, попавших в
промежуток от -
доx,
т.е. значения 0,1,2…k.
Следовательно,
.
Приx>n,
F(x)=1.
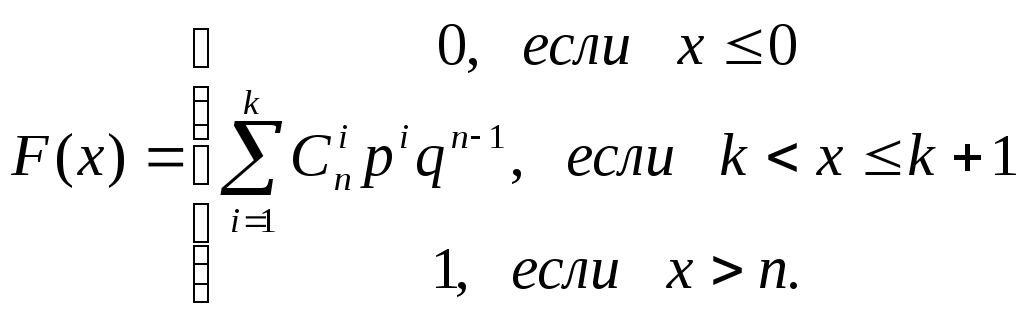
Задача 1.6.3
Случайная
величина Х
имеет плотность распределения,
пропорциональную х
при
0
и равную 0 при
и
.
а) Найти выражение для f(x)
б) Найти
М(х),
D(x),
.
Решение. а) Выражение плотности распределения имеет вид
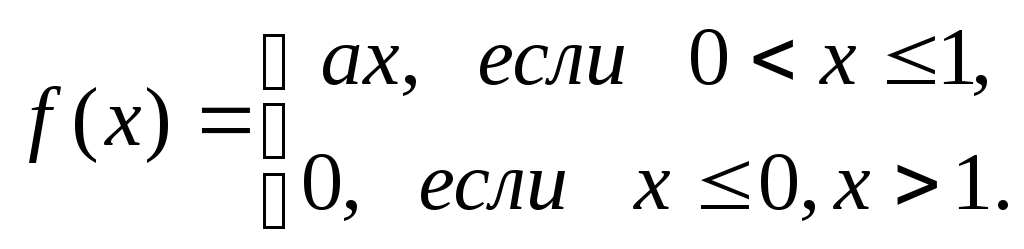
Пользуясь свойством плотности распределения, находим
откуда 1/2
б)
Математическое ожидание М(Х)=
Дисперсия
D(X)=
Задача 1.6.4
Задана функция распределения случайной величины X:
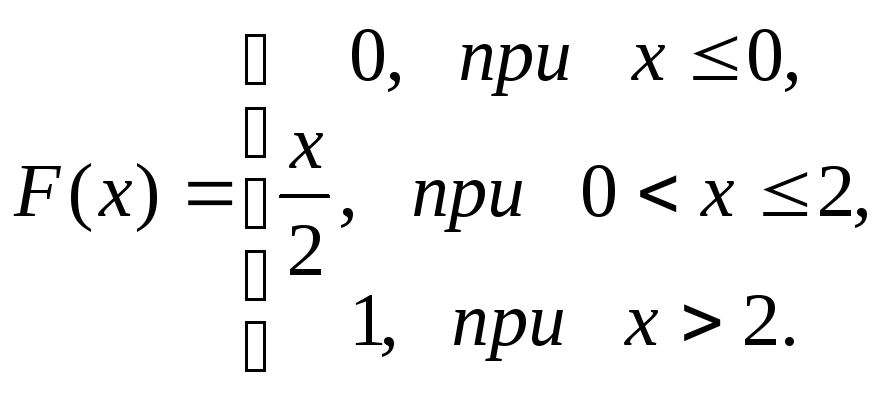
Найти вероятность того, что случайная величина Х примет значение в интервале (1;3).
Решение. Вероятность попадания случайной величины в интервал (1;3) по формуле (1.2) равна P(1<X<3)=F(3)-F(1)=1-1/2=1/2.