
- •1 Методические указания к самостоятельной работе над курсом
- •Основные формулы и теоремы
- •1.1 Классическое определение вероятности
- •1.2 Теоремы сложения и умножения вероятностей
- •1.3 Формула полной вероятности. Формула Бейеса
- •1.4 Схема испытаний Бернулли (повторение опытов)
- •1.5 Предельные теоремы
- •Оценим значение
- •1.6 Функция распределения случайной величины. Непрерывная случайная величина
- •1.7 Закон больших чисел. Предельные теоремы
- •1.8 Системы случайных величин
- •2 Расчётные задания Задача 2.1
- •Задача 2.2
- •Задача 2.3
- •Задача 2.4
- •Задача 2.5
- •Задача 2.6
- •Задача 2.7
- •Задача 2.8
- •Задача 2.9
- •Задача 2.10
- •Задача 2.11
- •Список литературы
- •Содержание
- •2.2 Расчётные задания 23
1.5 Предельные теоремы
Если число испытаний n велико , то применение формулы Бернулли приводит к громоздким вычислениям . В таких случаях пользуются предельными теоремами Лапласа. а) Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которые вероятность появления события равна р(о<р < 1), событие наступит ровно m раз, выражается приближенным равенством
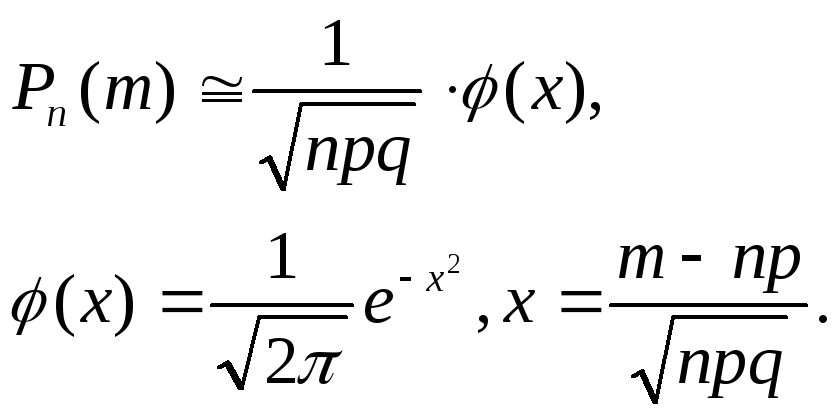
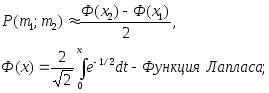 Функция
у(х) - четная,
т.е. у(-х)= γ(х).
При х>5 можно считать, что γ(x)=0.
б) интегральная
теорема Лапласа. Вероятность того, что
в n,
независимых испытаниях, в каждом из
которых вероятность появления.
события равна р, событие наступит не
менее m1
раз и не более
m2
раз, выражается приближенным равенствам
Функция
у(х) - четная,
т.е. у(-х)= γ(х).
При х>5 можно считать, что γ(x)=0.
б) интегральная
теорема Лапласа. Вероятность того, что
в n,
независимых испытаниях, в каждом из
которых вероятность появления.
события равна р, событие наступит не
менее m1
раз и не более
m2
раз, выражается приближенным равенствам
![]()
При
![]() >5
полагают Ф(х)=5. Функция Лапласа –
нечетная, т.е.
>5
полагают Ф(х)=5. Функция Лапласа –
нечетная, т.е.
Ф(-х)=-Ф(х), Ф(0)=0.
Если число испытаний
достаточно велико , а р - мало при, этом
![]() не
больше 10 (
не
больше 10 (![]() 10), то вероятность
10), то вероятность![]() можно найти приближенно по формуле
Пуассона:
можно найти приближенно по формуле
Пуассона: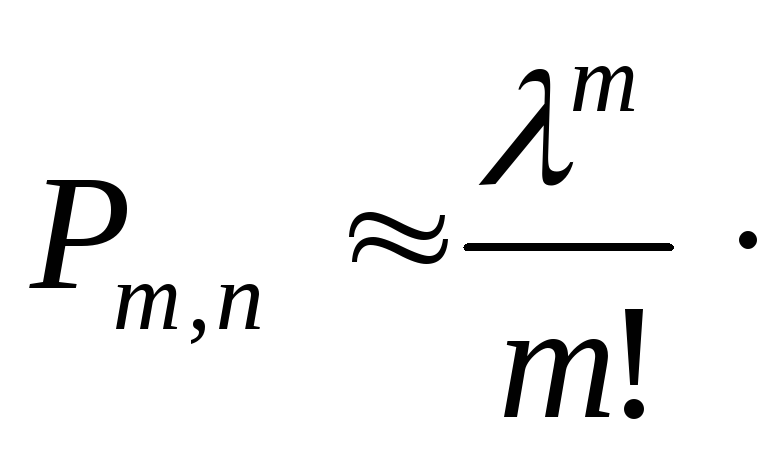
![]() .
.
Задача 1.5.1
Прибор состоят из 200 деталей, каждая из которых за врем t может выйти из строя с вероятностью р=0 01. Найти вероятность того, что за времяtвыйдут из строя: а) 3 детали; б) не более 3 деталей; г) от двух до четырех деталей включительно.
Р![]() ешение:В данном случаеn=200,m=0.01,q=0.99,m-
количество деталей , вышедших аз строя
за времяt. а)m=3;РЗ;200
по формуле Бернулли равно
ешение:В данном случаеn=200,m=0.01,q=0.99,m-
количество деталей , вышедших аз строя
за времяt. а)m=3;РЗ;200
по формуле Бернулли равно
Оценим значение
![]() - не более 3 деталей вышло из строя
- не более 3 деталей вышло из строя
![]()
Для вычисления каждого слагаемого
используем формулу Пуассона, определяя
значения вероятностей по таблице при
![]() и
приm=0,1, 2,3.
и
приm=0,1, 2,3.
Р200(![]() )
= 0.8572;
)
= 0.8572;
в){т > 2}- не менее двух деталей вышло из строя .Здесь следует перейти к противоположному событиюm<2. Тогда Р200(m>2)=1-Р0,2ОО –P1,200=0.5940.
г)2< m<1 от двух до
четырех деталей включительно за времяtвышли из строя следует
найти Р200 (2< m<
4)=Р2,200+Р3,200+Р4,200. Используя, формулу
Пуассона опять при![]() =2
иm=2,3,4 по таблице находим
=2
иm=2,3,4 по таблице находим
Р200![]()
Задача 1.5.2
Вероятность изделию быть, бракованным равна 0.05. Найти вероятность того, что среди 1000 изделий а) 40 бракованных; б) число бракованных находится в промежутке от 40 до 70 включительно; в) сколько изделий надо взять, чтобы с вероятностью, не менее 0,9 среди них оказалось не менее 50 бракованных?
Решение:Испытание изделий на брак удовлетворяет модели испытаний Бернулли Вероятность для каждого изделия быть бракованным, р=0.05, а набракованнымq=0.95. Испытаниям подвергаютсяn=1000 изделий.
a)m=40; Р
40,1000 находим по формуле Муавра Лапласа.
Определим необходимые величины:np=50;npq=47,5,
![]()
![]()
f(-1.45)=f(1.45)=0.1392.Окончательно
получаем![]()
б) Р1000 (40< m< 70) находим
по интегральной формуле Муавра –Лапласа
при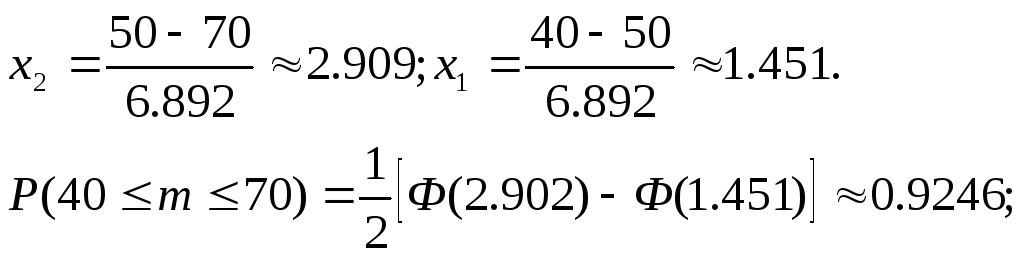
в) необходимо найти число n,удовлетворяющее условию
![]()

(Очевидно, что
![]() ).Следовательно
Ф(x2)=1. Получаем
).Следовательно
Ф(x2)=1. Получаем
![]()
По таблице, что Ф(t)=-0,8 приt=-1,29. Поэтому![]() и
после упрощения получаем
и
после упрощения получаем![]() Решив
это неравенство, найдем
Решив
это неравенство, найдем![]() Следует взять менее 1198 изделий.
Следует взять менее 1198 изделий.
