68

1 Методические указания к самостоятельной работе над курсом

«Теория вероятностей»

Основные формулы и теоремы

1.1 Классическое определение вероятности

Вероятность события А обозначается символом р или р(А).

При классическом определении вероятность события А равнаотношению числа случаев m , благоприятствующих ему из общего числа n равновозможных, единственно возможных и несовместных случаев, к числу n , т.е.

очевидно, что число 0P(А)1.

Задача 1.1.1

По телевидению передано 10 снимков, из них три снимка с искажениями. Какова вероятность, что два взятых на удачу снимка: а) не имеют искажений б) оба имеют искажения? в) один имеет искажение?

Решение: Два снимка из десяти можно выбратьn=способами (порядок не важен). Обозначим события: а) Событие А- обаснимка не .имеют искажения т.е. они выбраны из 7 качественных снимков.Это можно сделатьспособами. Следовательно,.б) Событие В - оба снимка имёю искажения, т.е. они взяты .из трех некачественных . Получим, откуда. в) СобытиеС - один имеет искажение и один не имеет искажение, т.е. один снимок взят из 3 , а 1 - из 7. По правилу произведения это можно сделатьспособами, поэтому

Задача 1.1.2

а)Сколько различных трехзначных чисел можно записать при помощи цифр 1; 2? б)Найти вероятность, что записано число 121. (Событие А).

Решение:а) Трехзначные числа - упорядоченные тройки элементов, образованные из цифр 1 и 2, размещения с повторениями из двух элементов по 3. Их числоб) Событию А благоприятствует один исходm=1. Поэтому.

1.2 Теоремы сложения и умножения вероятностей

Непосредственный подсчет вероятности, основанный на построении полной группы событий, практически редко может быть осуществлен. Поэтому основной задачей теории является рассмотрение различных теорем, с помощью которых вероятности одних событий определяются по вероятностямдругих событий. Важнейшие из них - теоремы сложения и умножения.Условная вероятность события А относительно события В равна:

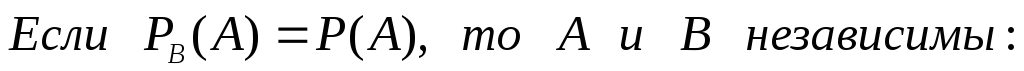
(1.2.1)

Выражение (1.2.1) получило название теоремы умножения вероятностей.

Вслучае произведения более чем двух событий теорема умножения вероятностей принимает вид

Событиянезависимы всовокупности, если(1.2.2)

Теорема сложения вероятностей: если события попарно несовместимы, то вероятность суммы событий равна сумме вероятностей этих событий:

(1.2.3)

Если несовместные события образуют полную группу, тосумма вероятностей этих событий равна 1. В частности, для двух, противоположных событий Аи имеет место равенство , и поэтому вероятность противоположного события вычисляется по формуле

Если события совместны, то формулы для вероятности суммы этих событий усложняются. Например, вероятность суммы двух местных событий равна

_,

а вероятность суммы трех совместных событий

Задача 1.2.1

Из коробки, содержащей 5 красных и 3 черных шариковых ручки, извлекают 2 ручки. Найти вероятность того, что: а) обе ручки красные. 6) ручки разных цветов. Рассмотреть 2 случая: 1) извлеченная первой ручка не возвращается в коробку; 2) извлеченная первой ручка возвращается в коробку перед извлечением второй.

Решение. Введём обозначения для событий: А - обе ручки красного цвета; В - ручки разных цветов. Следует определить Р(А) и Р(В)

Введём события, связанные с извлечением одной ручки: А1-первая ручка: красная; - первая ручка чёрная, А2 - вторая ручка красная;вторая ручка черная. Тогдаи.

Применяем формулы (1.2.1) и (1.2.3).

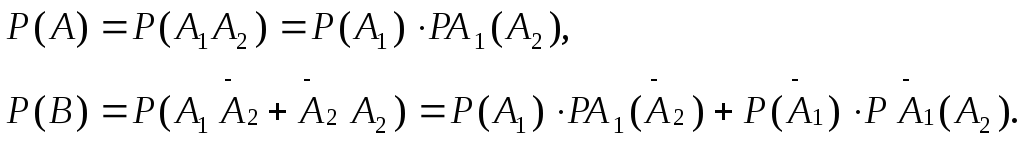
В данном случае события инесовместны.

1 случай.Так как после наступленияручка не возвращается, то в коробке окажется 7 ручек. Из которых 4 красных и поэтому

2 случай. (так как после наступленияручка возвращена в коробку).

а) . б).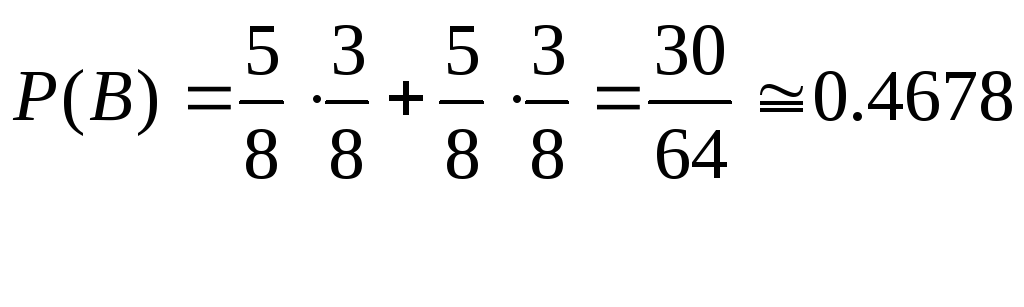

Задача 1.2.2

Прибор собирается последовательно четырьмя рабочими. Независимо от остальных 1-й может допустить брак вероятностью 0,1,2-й и 3-й - с вероятностью 0,09, а 4-й -0,15. Готовый прибор относится к I сорту, если ни один рабочий не допустил брак, ко II, если брак допущен 2-м или 3-м рабочим, к III сорту, если брак допустили 1 -й или 4-й рабочие и признаётся негодным в остальных случаях. Найти вероятности следующих событий: А - прибор признан I сорта; В - II сорта; С - Ш сорта;D- прибор признан негодным.

Решение: Обозначим Через Аi событие, состоящее в том, что i-ый рабочий не допустил брак, тогда-i-ый рабочий допустил бракi=1,2,3,4 . В условии дано Р(А1) =01; Р(А2)= Р(АЗ)=0,09 ; Р(А4)=0,15. Тогда P(A1)=0.9;P(A2)=P(A3)=0.91; Р(A4) = 0.85

Интересующие нас события можно представить следующим образом: A=A1А2А3А4; B=A1A2A3A4+А2А3А4;C=A1A2A3A4+A2A3А4. Событие D противоположно сумме событий А+В+С, т.е. D= A+B+C:

Применяем формулы (1.2.2) для независимых событий и (1.2.3) для несовместных событий-слагаемых в выражениях для В и С, получим

Задача 1.2.3

Вероятность того, что проходящая машина потребует заправки в данном пункте, равна 0.3. Сколько должно пройти машин чтобы с вероятностью не меньшей, чем 0.9 можно было утверждать, что хотя бы одна потребует заправки?

Решение; Введем обозначения для событий : Аi –i-я машина потребует заправки и С - хотя бы одна машина из и потребует заправка. Тогда С=А1+А2+...+Аn.

Однако все слагаемые совместны, поэтому перейден противоположному событию С -“ни одна машина из n потребует заправки” получим

События A1 ,А2,..., An , а следовательно , _ A1 А2…Аn независимы и имеют одну и ту же вероятность

Поэтому По условию задачи те. Решая это неравенство, найдем последовательно nlg0.7lg0,1, откуда. Окончательно получаемn=7.