§12. Кодирование сообщений словами переменной длины

Пусть имеется множество передаваемых сообщений S={s_j}, i=1,…,m, причем известна вероятность p_j появления каждого из сообщений на входе устройства кодирования (при соблюдении условия нормировки ). Пусть также имеется множество двоичных кодовых слов переменной длины, используемых для кодирования этих сообщенийK={k_j}, причем l_j =l(k_j) – длина кодового слова k_j, соответствующего сообщению s_j.

Тогда в качестве критерия эффективности кодирования сообщений множества S кодовыми словами множества K выступает величина λ_k^S , называемая средней длиной кодового слова и определяемая следующим образом:

(1.3)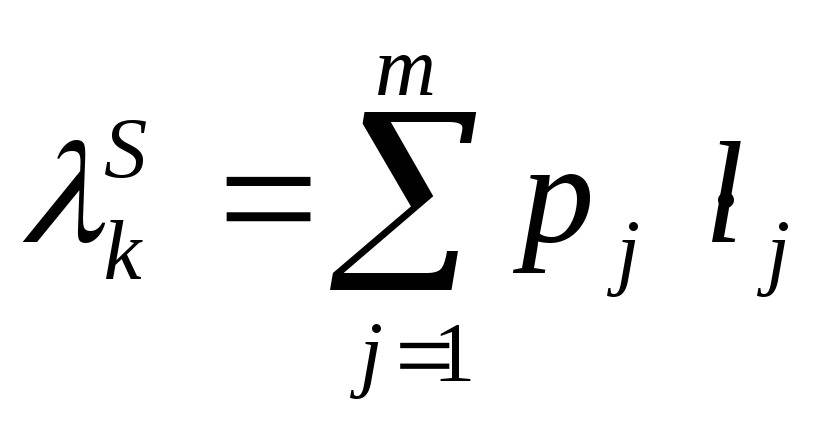

Рассмотрим пример. Пусть множество сообщений S={s₁, s₂, … , s₁₀} характеризуется вероятностями появления, определяемыми по следующей формуле:

(1.4)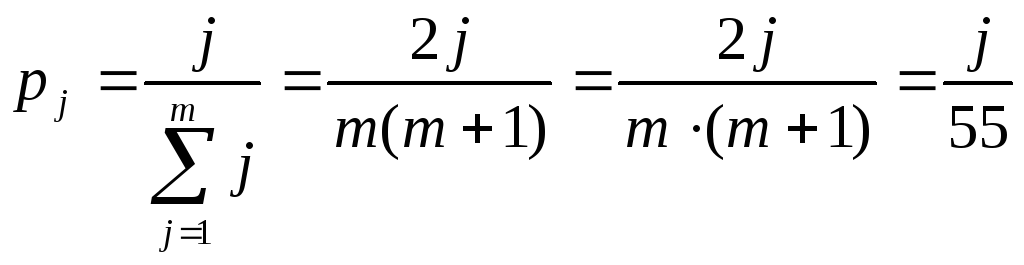

(Можно проверить, что условие нормировки при этом соблюдается).

Воспользуемся для кодирования данных сообщений кодовыми словами рассмотренного выше префиксного кода так, как это показано в таблице 1.1.

Таблица 1.1

Сообщение sj	Вероятность pj	Кодовое слово kj	Длина кодового слова lj
s1	1/55	111111	6
s2	2/55	111110	6
s3	3/55	11110	5
s4	4/55	1110	4
s5	5/55	1001	4
s6	6/55	1000	4
s7	7/55	110	3
s8	8/55	101	3
s9	9/55	01	2
s10	10/55	00	2

По формуле (4.3) получим:

(бит/сообщение)

Если бы мы закодировали сообщения равномерным кодом, то, согласно формуле (1.1) нам потребовались бы кодовые слова длины (бит/сообщение), т.е. кодирование словами переменной длины оказывается более эффективным.

Заметим, что в приведенном примере кодовые слова ставились в соответствие сообщениям таким образом, что их длина оказывалась обратно пропорциональной вероятности появления каждого из сообщений. Тем самым обеспечивалось наиболее экономное кодирование, поскольку при данном способе распределения значение величины λ_k^S минимально.

Как же выбирать кодовые слова в общем случае, чтобы для заданных вероятностей p₁, p₂, … , p_m обеспечить по возможности меньшую среднюю длину кодового слова, т.е. λ_k^S → min?

Заметим, что если , то минимальную среднюю длину кодового словаλ_k^S обеспечивает равномерное двоичное кодирование. На каждом шаге двоичного кодирования производится разбиение множества сообщений на два подмножества, причем одному из них приписывается единица, а другому – ноль. Таким образом, на каждом шаге производится кодирование подмножеств равномерным кодом длиной в один двоичный знак. Отсюда следует принцип: нужно стремиться так производить разбиение на два подмножества, чтобы суммарные вероятности подмножеств были одинаковыми или как можно более близкими друг к другу.

Рассмотрим две процедуры экономного кодирования, основанные на использовании этого принципа.

§13. Процедура Шеннона-Фано

В этом алгоритме предварительно производится упорядочивание сообщений по возрастанию или убыванию вероятностей p_j. Разбиение на подмножества производится путем выбора разделяющей границы в упорядоченной последовательности так, чтобы суммарные вероятности подмножеств были по возможности одинаковыми. Кодовое дерево, построенное этим методом для примера в таблице 1.1, приведено на рис.1.5. Возле каждой вершины дерева указывается суммарная вероятность соответствующего подмножества.

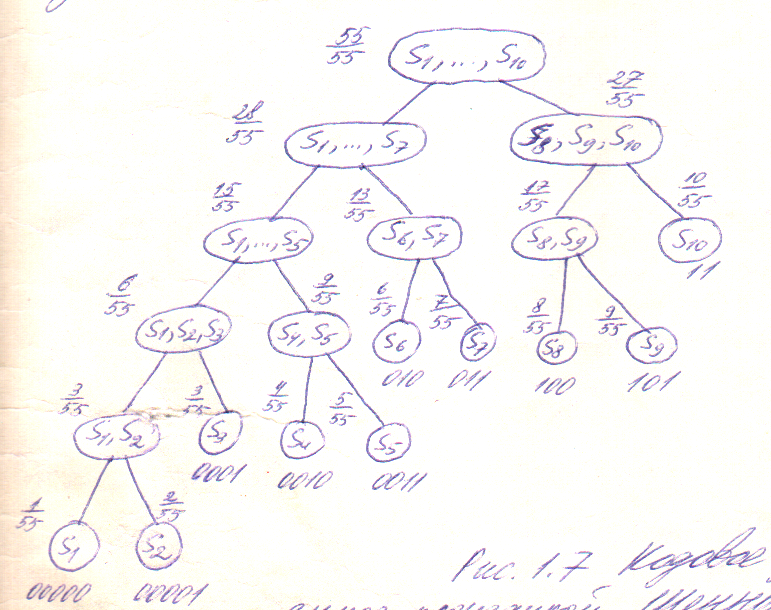
Рис.1.5

Кодовое дерево в процедуре Шеннона-Фано

Выполнив расчеты по формуле 1.3, получим: λ_k^S=3,145 (бит/сообщение). Таким образом, код, полученный при помощи процедуры Шеннона-Фано, оказывается более экономным, чем код из таблицы 1.1.