РГР ТОЭ 1

Задание:

1.Определить все токи методом контурных токов.

2.Определить все токи методом узловых напряжений, приняв потенциал 4-го узла равным нулю.

3.Произвести проверку по законам Кирхгофа.

4.Составить баланс мощностей.

5.Определить ток I1 методом эквивалентного генератора.

6.Начертить в масштабе потенциальную диаграмму для любого контура, включающего в себя две ЭДС.

Исходные данные:

R1=40 Ом E1=-50 В Ik1=0 А

R2=70 Ом E2=0 В Ik2=-2 А

R3=20 Ом E3=0 В Ik3=0 А

R4=80 Ом E4=0 В

R5=70 Ом E5=0 В

R6=80 Ом E6=150 В

E4 E5

5

4

R4 R5 R6

E3 R3

1 3

Jk1 E1 3 Е2 E6

1 R1 R2 2

Jk2 Jk3 6

4

R6

Схема с произвольно выбранными направлениями токов

1. Расчет цепи методом контурных токов

Число ветвей схемы

Число ветвей схемы, содержащих источник тока

Число узлов

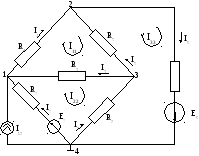
Составим линейно независимые уравнения по первому закону Кирхгофа, число которых равно числу узлов без единицы (у – 1 = 3):

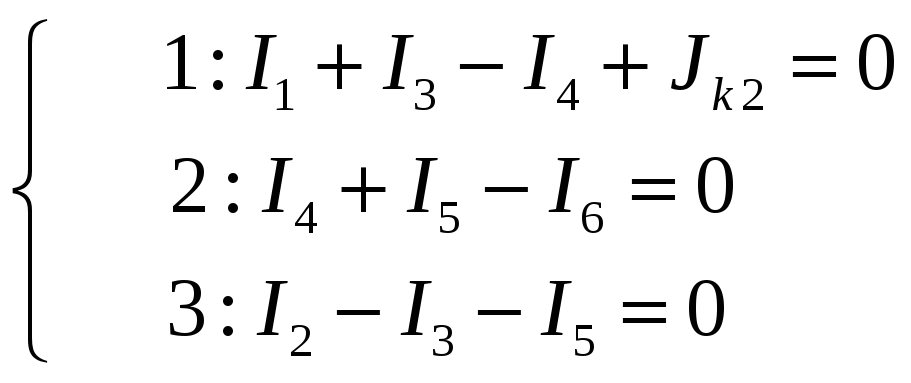
По второму закону Кирхгофа составляем уравнения, число которых равно

I₁₁R₁₁ + I₂₂R₁₂ + I₃₃R₁₃ = E₁₁

I₁₁R₂₁ + I₂₂R₂₂ + I₃₃R₂₃ = E₂₂

I₁₁R₃₁ + I₂₂R₃₂ + I₃₃R₃₃ = E₃₃

Определим собственные и взаимные сопротивления:

R₁₁=R₃+R₄+R₅=20+80+70=170 Ом

R₂₂=R₁+R₂+R₃=40+70+20=130 Ом

R₃₃=R₂+R₅+R₆=70+70+80=220 Ом

R₁₂=R₂₁= - R₃= -20 Oм R₁₃=R₃₁= -R₅= -70 Oм R₃₂=R₂₃= -R₂= -70 Oм

Определим собственные ЭДС:

E₁₁=0 В E₂₂=E₁+J_к2∙R₁ = -50+(-2)*40 = -130 В E₃₃= Е6=150 В

Составим матрицу и найдем контурные токи, используя программу Gauss:

I₁₁≈ -0,11776 A; I₂₂≈-0,7175 A; I₃₃≈ 0,49099 A.

Найдем реальные токи I₁, I₂, …, I₆:

I₁= I₂₂ − J_к2=-0,7175-(-2) ≈1,2825 А

I₂= -I₂₂+I₃₃= -(-0,7175)+0,49099≈1,20849 А

I₃= -I₂₂ + I₁₁= -(-0,7175)+0, 11776≈0,83526 А

I₄= I₁₁= 0,11776 А

I₅= I₃₃ − I₁₁=0,49099 -0,11776 = 0,37323 А

I₆= I₃₃ =0,49099 А

2. Расчет цепи методом узловых потенциалов

Определим число уравнений и запишем их:

n_уз=У-1=4-1=3

G₁₁φ₁ + G₁₂φ₂ + G₁₃φ₃ = J₁₁

G₂₁φ₁ + G₂₂φ₂ + G₂₃φ₃ = J₂₂

G₃₁φ1 + G₃₂φ₂ + G₃₃φ₃ = J₃₃

Используя обобщенный закон Ома, определим токи во всех ветвях:

; ; ; ; ;

Определим собственные и взаимные проводимости:

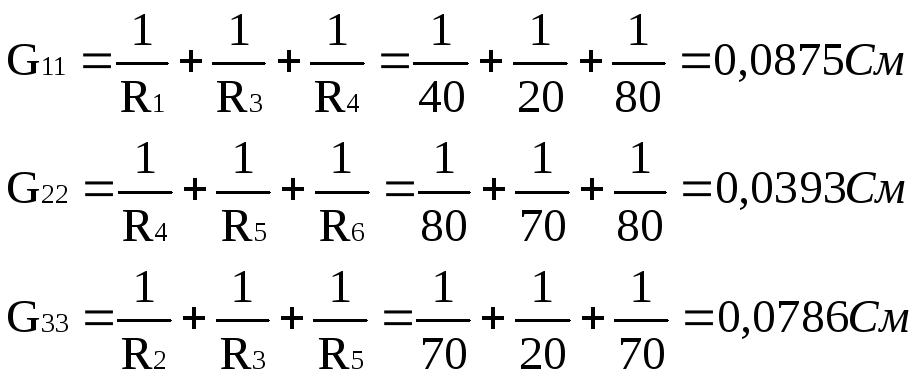
Определим приведенные токи:

J₁₁ = E₁/R₁+J_к2= -50/40-2= -3,25 A

J₂₂= -E₆/R₆= -150/80 A

J₃₃ = 0

Составим матрицу и, используя программу Gauss, определим потенциалы точек:

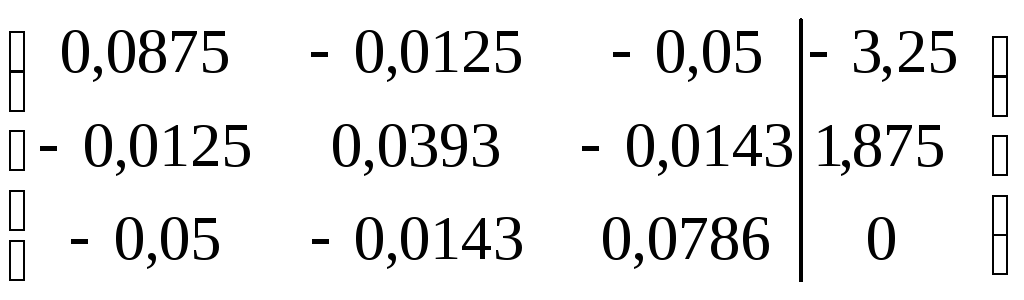
φ₁=-101,28 В φ₂=-110,69 В φ₃=-84,57 В φ₄=0 B

А

A

A

A

A

A

Таблица токов

Токи	I1, A	I2, A	I3, A	I4, A	I5, A	I6, A
по методу контурных токов	1,2825	1,20849	0,83526	0,11776	0,37323	0,49099
по методу узловых потенциалов	1,28	1,208	0,836	0,118	0,373	0,491

3.Проверка по законам Кирхгофа

По первому закону Кирхгофа:

для 1 I₁+I_k2+I₃-I₄=0 1,2825 -2+0,83526-0,11776≈0

для 2 I₄+I₅-I₆=0 0,11776+0,37323-0,49099≈0

для 3 I₂-I₃-I₅=0 1,2825-0,83526-0,37323≈0

По второму закону Кирхгофа:

1: I₂R₂+I₅R₅+I₆R₆=Е6 1,20849*70+0,37323*70+0,49099*80≈150 (выполняется)

2: -I₃R₃+I₁R₁-I₂R₂=E₁ -0,83526*20+1,2825*40-1,20849*70≈-50 (выполняется)

3: I₃R₃+I₄R₄-I₅R₅=0 0,83526*20+0,11776*80-0,37323*70≈0 (выполняется)

Законы Кирхгофа выполняются, значит, токи найдены правильно.

4. Баланс мощности.

Рнагр =I₁²R₁+I₂²R₂+I₃²R₃+I₄²R₄+I₅²R₅+I₆²R₆

Рнагр=Вт

Рист =E₁I₁+E₆I₆+I_k2U₁₄=E₁I₁+E₆I₆+I_k2()

Рист= Вт

Баланс мощности соблюдается.

5. Расчет тока I₁ методом эквивалентного генератора.

Определим U_xx (при отсутствии нагрузки R₁), используя метод узловых потенциалов.

2

I₄

R₅

R₄

I₅

I₃

R₃

1

R₆

3

E₆

R₂

I₂

I₆

I_k2

Uxx

E₄

E₄

4

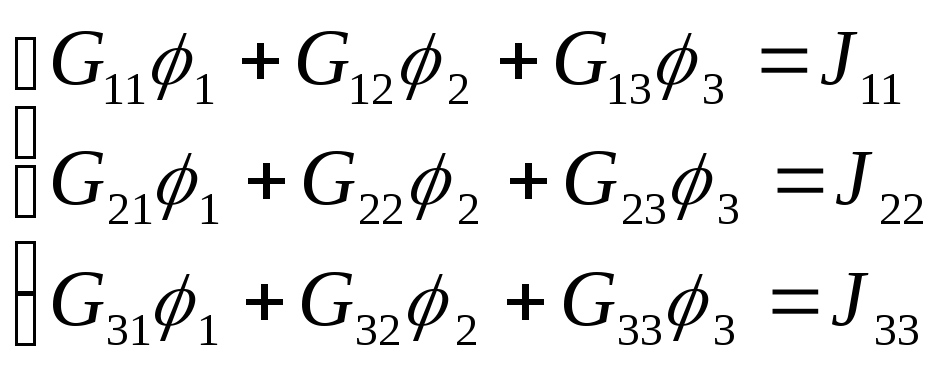
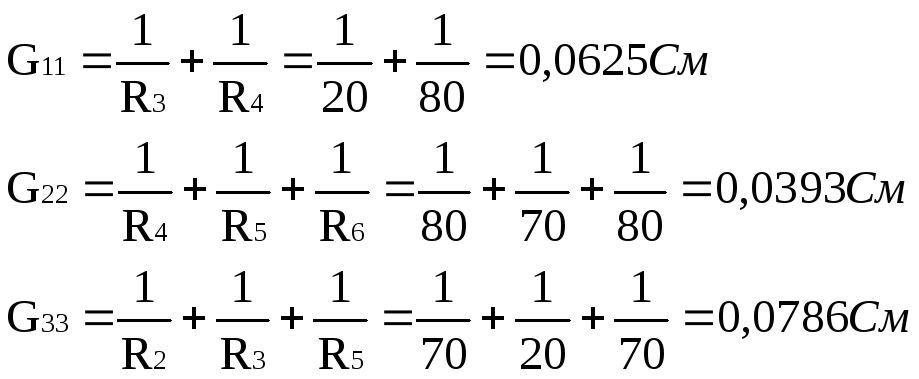
Определим приведенные токи:

J₁₁ = J_к2 = -2 A

J₂₂= -E₆/R₆=-1,875 A

J₃₃ = 0

Составим матрицу и, используя программу Gauss, определим потенциалы точек:

φ₁=-172,6595 В φ₂=-152,71453 В φ₃=-137,641 В

U_xx =Е1-φ₁ =-50+172,6595=122,65595 В

Для определения R_экв преобразуем треугольник сопротивления в звезду сопротивления:

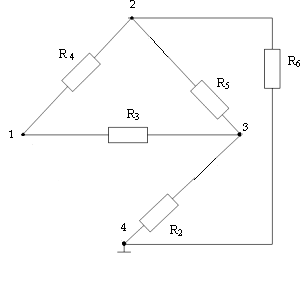
По формулам преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений определяем R₇, R₈ , R₉ :

6. Потенциальная диаграмма контура 4-1-3-2-4.

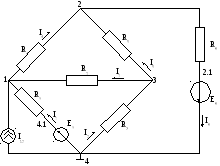
φ₄=0 В

φ_4.1=-I₁R₁= -51,3 В

φ₁= φ_4.1-Е₁= -51,3+50= -1,3 В

φ₃= φ₁+ I₃R₃= -1,3+0,83526*20=15,4 В

φ₂= φ₃-I₅R₅=15,4-0,37323*70= -10,7 В

φ_2.1= φ₂ –I₆R₆=-10,7-0,49099*80=-49,9 В