§7. Линейные преобразования векторных пространств

1. Основное определение.

Ранее рассматривали функции, т.е. правила, по которым ставилось в соответствие число. Теперь обобщим это понятие.

Определение 1. Пусть – –мерному векторному пространству поставлен в соответствие (тому же пространству). Соответствие назовём преобразованием пространства .

Преобразование называется линейным, если

1. 

2. 

Примеры:

1. Пусть – подпространство в трехмерном пространстве . 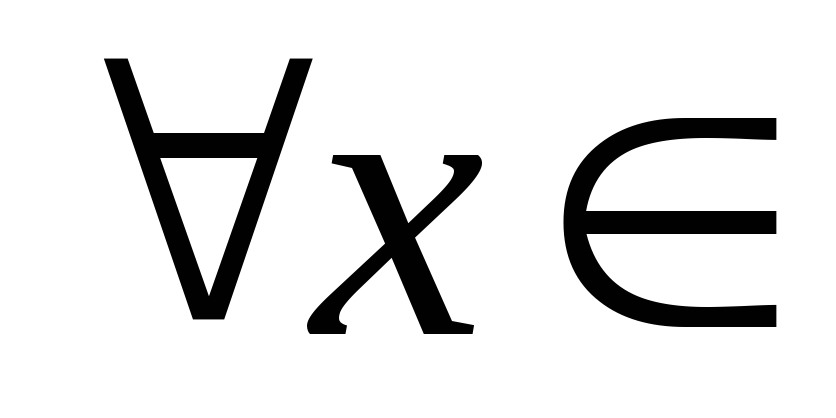соответствующему поставим в соответствие его проекцию на 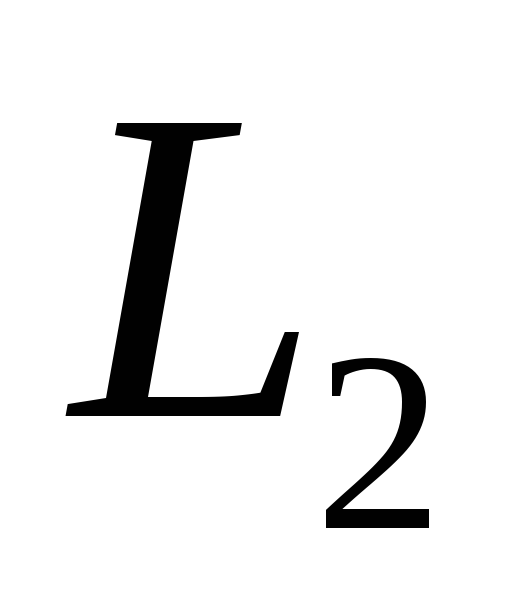: 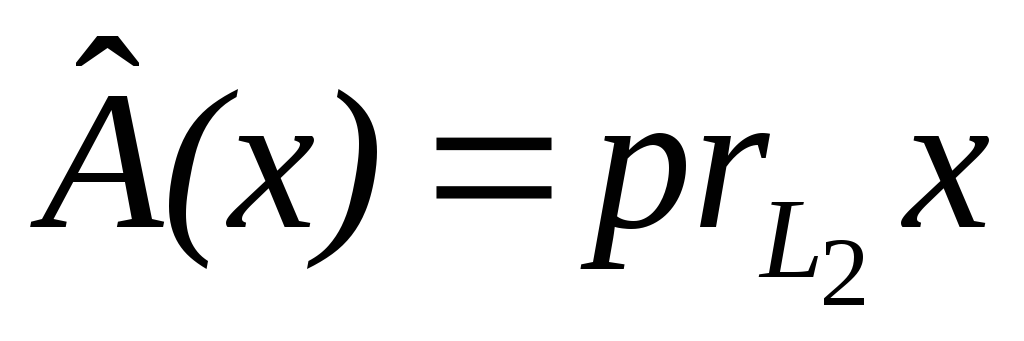. Это линейное преобразование, свойства 1, 2 – легко проверяются.

2. Пусть 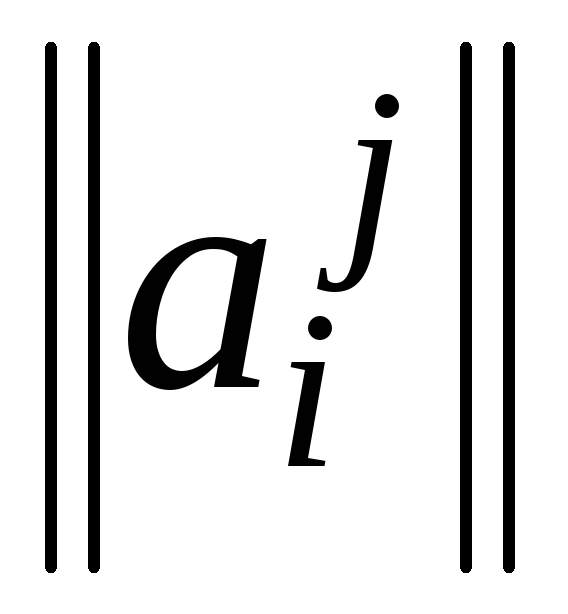– матрица , – пространство – чисел . . Это линейное преобразование.

3. – пространство многочленов степени . Пусть – т.е. производная многочлена. Линейность – очевидна.

4. , – линейность из свойств интеграла.

Это пример преобразования в бесконечномерном пространстве. Далее – лишь конечномерные.

2°. Матрица линейного преобразования.

Пусть – базис в и – линейное преобразование. Каждый . Векторы не зависят от и они могут быть разложены по базису : , т.е. если , где

.

(1)

Определение 2. Матрицей линейного преобразования в базисе называется матрица (1), столбцы которой – координаты образов векторов в базисе .

Утверждение 1. Выбор базиса в устанавливает взаимно однозначное соответствие между линейными преобразованиями этого пространства и квадратными матрицами порядка .

Доказательство: Итак, показано, что если выбран базис, то любому преобразованию соответствует матрица (1). В соответствии с примером 2 из пункта 1, любой матрице соответствует линейное преобразование. Осталось проверить, что разным матрицам соответствуют разные преобразования. Пусть и – разные преобразования, т.е. . Если они имеют одну и ту же матрицу , то для имеем: ,то противоречит.

При изменении базиса матрица линейного преобразования, вообще говоря, изменяется.

Примеры:

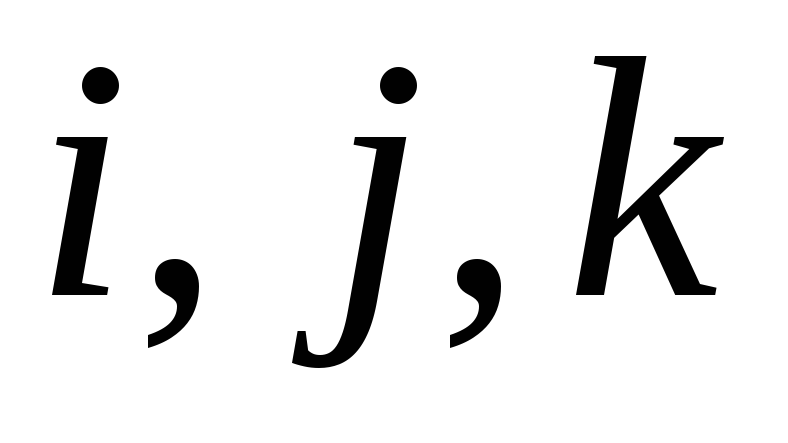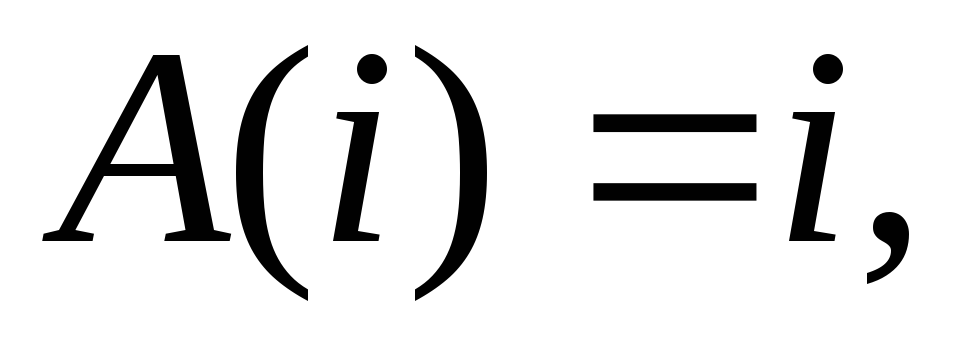
1. Пусть – трёхмерное пространство с базисом , а – оператор проектирования на плоскость . Тогда матрица .

2. Если – тождественное преобразование, то

3. – многочлены степени . .

Базис : .

Тогда .

Таким образом, матрица .

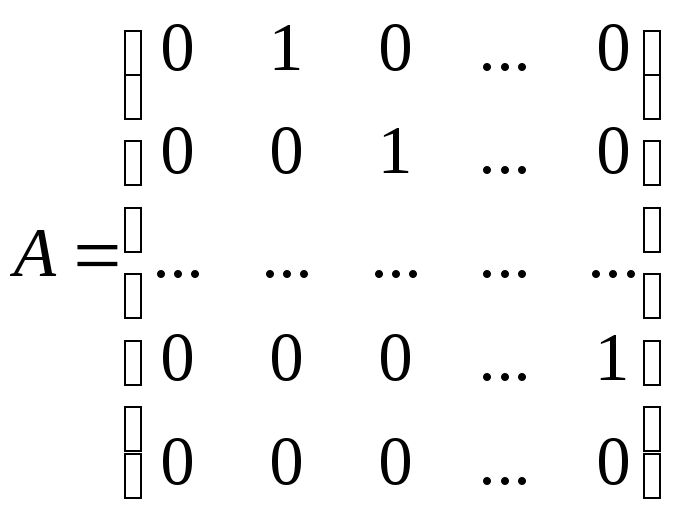Рассмотрим формулы преобразования при переходе к другому базису. Пусть . Пусть .

Свойства.

1°. Ранг матрицы линейного оператора при переходе от одного базиса к другому является инвариантом.

2°. Определитель матрицы линейного оператора инвариантен.

Доказательство. Следует из свойств ранга и определителя.

3°. Сложение и умножение линейных преобразований.

Определение 3. Произведением линейных преобразований и называется .

Очевидно, что – линейное преобразование: .

Если – единичное преобразование, то .

Можно определить степени преобразований: .

Тогда .

Пусть в базисе преобразованию соответствует матрица , , . Выразим через и .

По определению

Далее , т.е. есть сумма произведений элементов –ой строки на –ый столбец – произведение матриц все свойства произведения матриц переносятся на преобразования (ассоциативность, не коммутативность).

Определение 4. Суммой преобразований и называется . Легко показать, что матрица

Операции сложения и умножения удовлетворяют обычным свойствам сложения и умножения матриц. Это следует из того, что между матрицами и преобразованиями есть взаимно однозначное соответствие. Нулевое преобразование – нулевая матрица.

Утверждение 2. Множество преобразований линейного пространства образует кольцо, называемое кольцом эндоморфизмов.

Определение 5. Произведением линейного преобразования на число называется преобразование .

Свойства: очевидны.

Утверждение 3. множество линейных преобразований образует линейное пространство размерности .

Следствие. Матрицы – линейно зависимы множеств степени