Примеры.
1) В пространстве
геометрических векторов с обычным
скалярным произведением неравенства
Коши–Буняковского и Минковского имеют
вид:
, 
.
Первое неравенство
в силу
означает, что
,
второе − что длина стороны треугольника
не превосходят суммы длин двух других
сторон.
2) В
неравенства Коши–Буняковского и
Минковского дают:
.
3) В
с обычным скалярным произведением и
имеем
неравенство Коши–Буняковского
;
неравенство Минковского
.
4) В
со скалярным произведением с положительно
определённой симметрической матрицей
имеем
неравенство Коши–Буняковского
;
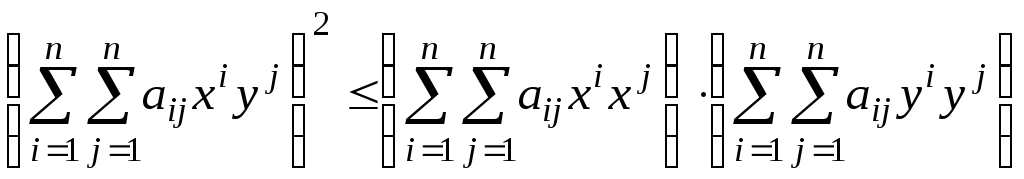неравенство Минковского
.
Замечание.
Если векторное пространство
дано над полем
,
то аналогично строится теория унитарных
(или эрмитовых)
пространств. В этом случае аксиомы 1) и
4) принимают соответственно вид:
1)
;
4)
и
,
если
.
Отметим, что неравенство Коши–Буняковского в этом случае принимает вид:
.
В
–мерном
комплексном координатном пространстве
C
стандартное скалярное произведение
векторов
C
задается формулой
.
2. Ортогональные и ортонормированные системы векторов.
Из неравенства Коши–Буняковского следует, что корректно можно ввести следующее
Определение 3.
Для любых
принадлежащих евклидовому пространству
E
определен угол
между ними:
.
Определение 4.
Элементы
E
называются ортогональными,
если их скалярное произведение равно
нулю, то есть
.
Тогда
.
Очевидно, что если
ортогонален
,
то
ортогонален
.
Лемма 1.
Нулевой вектор ортогонален любому
вектору из E
и является единственным вектором,
обладающим этим свойством.
Доказательство самостоятельно.
Определение 5.
Сумму
двух ортогональных векторов
назовем гипотенузой
треугольника, построенного на векторах
.
Лемма 2. Квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
.■
Обобщение.
Если
E
− взаимно ортогональны
.
Определение 6.
Система векторов евклидова пространства
E
называется
ортогональной,
если она либо состоит из одного вектора,
либо её векторы попарно ортогональны.
Теорема 3. Всякая ортогональная система ненулевых векторов евклидова пространства является линейно независимой.
Доказательство:
Пусть
− ортогональная система векторов и
пусть
с некоторыми
постоянными
.
Умножая это равенство скалярно на
,
получаем
.
Т.к.
все
− линейно независимы. ■
Определение 7. Ортогональная система, состоящая из векторов единичной длины, называется ортонормированной.
Определение 8.
В
–мерном
евклидовом пространстве E
система
ортонормированных векторов образует
ортонормированный
базис.
Теорема 4.
Во всяком
–мерном
евклидовом пространстве E
существует ортонормированный базис.
Доказательство.
Т.к. пространство E
−
–мерное,
то существуют
векторов
,
которые линейно независимы. Покажем,
что можно построить векторы
,
получающиеся как линейные комбинации
,
которые образуют ортонормированный
базис. Доказательство методом
математической индукции:
Если
− очевидно, т.к.
Пусть удалось
построить
векторов
,
которые попарно ортогональны, их нормы
равны единице, и получены как линейные
комбинации
.
Будем искать вектор
.
Выберем
так, чтобы
был ортогонален
.
Умножая
скалярно на
,
в силу ортонормированности
имеем:
//т.к.
//
.
Очевидно, что
полученный
,
т.к. он является линейной комбинацией
система
− ортонормированная и получена как
линейная комбинация
.
■
Замечание 1. В доказательстве теоремы 4 использовался следующий алгоритм ортогонализации системы векторов, известный как алгоритм Грамма–Шмидта:
пусть
− линейно независимы. Тогда попарно
ортогональные единичные вектора
получаются по следующим формулам:
|
|
(4) |
Замечание 2.
В любом евклидовом пространстве можно
построить много ортонормированных
базисов. Примером ортонормированного
базиса в
с обычным скалярным произведением могут
служить вектора
Рассмотрим
произвольный ортонормированный базис
-мерного
евклидова пространства E
.
Пусть
E
− произвольный вектор и
.
Умножая обе части
равенства скалярно на
получим:
,
т.е. координаты
произвольного вектора относительно
ортонормированного базиса равны
скалярным произведениям этого вектора
на соответствующие базисные векторы.
Поскольку скалярное произведение
на вектор
,
естественно назвать проекцией
на
,
то, следовательно, координаты произвольного
относительно ортонормированного базиса
равны проекциям этого элемента на
соответствующие базисные элементы.
Таким образом, ортонормированный базис похож на ортонормированный базис в пространстве геометрических векторов.