
- •Моделирование в химической технологии и расчёт реакторов
- •Постановка задачи
- •Поверхность отклика
- •Поверхность отклика типа «седло»
- •Поисковые методы для функции одной переменной
- •Метод сканирования
- •Модернизированный метод сканирования
- •Метод сканирования
- •Модернизированный метод
- •Метод дихотомии (половинного
- •Метод дихотомии (половинного
- •Метод золотого сечения
- •Коэффициент 0,618 получается из условия постоянства отношения интервалов
- •Следует отметить, что значения х2 и х3 совпадают, а
- •Сравнение различных методов
- •Поисковые методы для функции многих переменных
- •Типы рельефа
- •Метод Гаусса – Зейделя (метод покоординатного поиска)

Моделирование в химической технологии и расчёт реакторов

 МЕТОДЫ ОПТИМИЗАЦИИ ХИМИКО- ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И НАХОЖДЕНИЯ ЭКСТРЕМУМА (МИНИМУМА ИЛИ
МЕТОДЫ ОПТИМИЗАЦИИ ХИМИКО- ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И НАХОЖДЕНИЯ ЭКСТРЕМУМА (МИНИМУМА ИЛИ

Постановка задачи
Исследование химико-технологических процессов завершается поиском оптимальных условий его осуществления
Если сформулирована зависимость
у = f(х1, х2, ... хr),
то оптимизация заключается в подборе таких значений х1, х2, ... хr, при которых у
будет оптимальным (т.е. минимальным или максимальным)
Кроме того, методы оптимизации используются при параметрической идентификации нелинейных моделей

Поверхность отклика
y
x2
X2
x1
X1
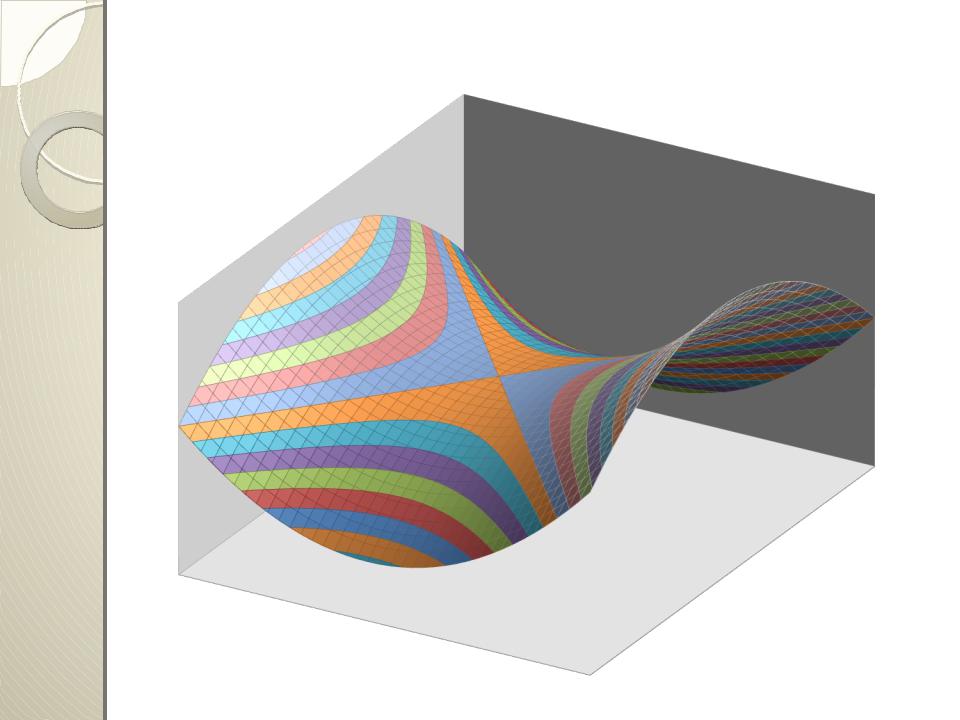
Поверхность отклика типа «седло»

Поисковые методы для функции одной переменной
Пусть функция у = f(х) в возможной области изменения аргумента имеет один экстремум
Для поиска экстремума функции одной переменной могут

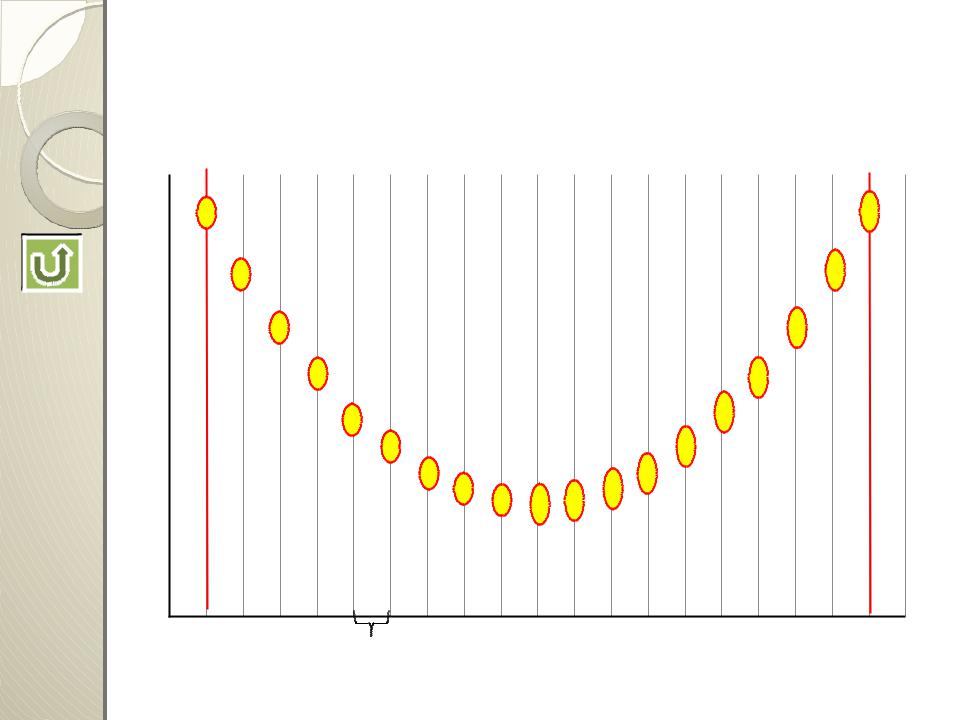
Метод сканирования
Если наименьшее изменение х, которое
приводит к ощутимому изменению у, то область поиска хmax - xmin можно разбить на
(xmax - xmin)/ интервалов и исследовать у на границе каждого интервала

Сравнивая найденные значения у, выбирают из них оптимальное 




Такой метод называется сканированием (обеганием)
Этот метод
Модернизированный метод сканирования
Известен ряд вариантов этого метода, позволяющих уменьшить вычислительную работу при сканировании
Можно, например, увеличить шаг поиска в 2r раз и проводить расчеты при “крупных” шагах в 2r
Проведя расчеты, наблюдают за величиной у
Найдя широкую “оптимальную” область, начинают движение к ней, уменьшив шаг в два раза - до 2r-1
Такую процедуру повторяют до получения узкого интервала вблизи экстремума
Метод сканирования |
|
||||||||
y |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
8 |
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
7 |
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
6 |
|
|
5 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
|
|
|
6 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
4 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
9 |
|
1 |
1 |
3 |
|
|
|
|
|
1 |
2 |
|
|
|
|||
|
|
|
1 |
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
Xmin |
|
|
|
|
|
|
|
Xma |
x |
|
|
|
|
|
|
|
|
x |
|
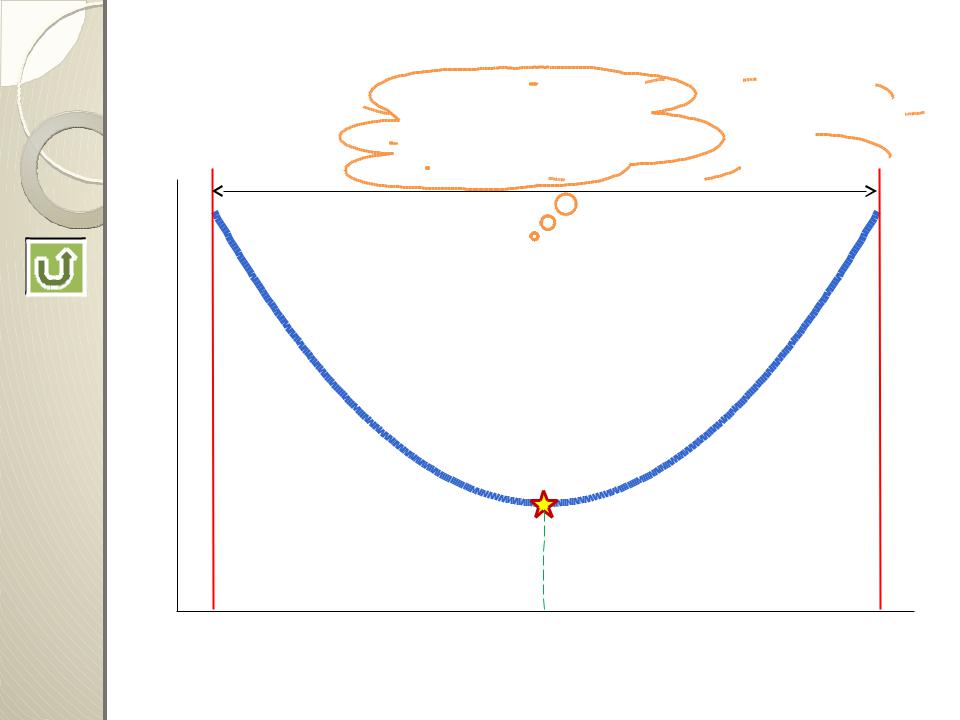
График зависимости у = f(х) |
|
|
|
||
|
|
Интервал |
|
|
|
y |
|
неопределённости |
|
|
|
|
|
|
|
|
|
X |
min |
X |
X |
ma |
x |
|
|
|
|
||
|
|
|
x |
|
|
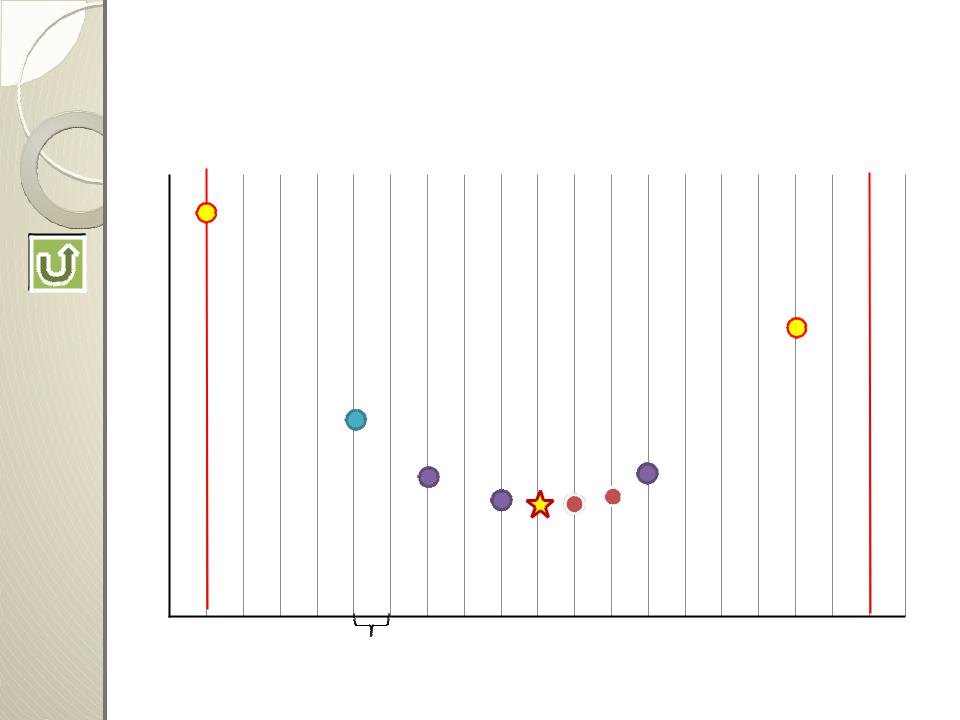
Модернизированный метод |
|
|
|
сканирования |
|
|
|
y |
|
|
|
Xmin |
|
Xma |
x |
|
|
x |
|
