2.5. Анализ автокорреляционной функции

Временным рядом называется последовательность наблюдений, упорядоченная по времени: y₁, y₂, …, y_n, где y_t – числа, представляющие наблюдение некоторой переменной в n равностоящих моментов времени t=1,2,…,n. Важнейшей характеристикой временного ряда является автокорреляционная функция:

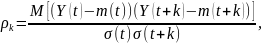
• _где 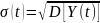, k=0,1,…,n-2; t=2,3,…,n.

Величина k, определяющая временной интервал между случайными величинами Y(t) и Y(t+k), для которых вычисляется коэффициент корреляции ρ_k, называется лагом.

Значения автокорреляционной функции:

Таблица 2. Значения автокорреляционной функции

Лаг	Коэффициент автокорреляции (АКФ)
1	0,12
2	–0,01
3	–0,03
4	0,09
5	–0,07
6	0,37
7	-0,08
8	0,07
9	–0,07
10	–0,06
11	0,05
12	0,77

График 5. Автокорреляционная функция

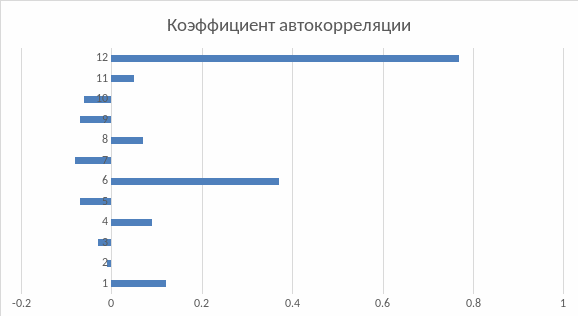
Как видно, между данными есть корреляция, и можно предположить, что между ними существует и сезонная зависимость. Согласно автокорреляционной функции, сезонные колебания будут повторяться каждые 12 месяцев (т.к. наибольшее значение – при лаге №12, равное 0,77). Следовательно, прогноз можно делать на 1 год.

2.6. Определение сезонной составляющей ряда (сезонных индексов)

Предположим, что исходный ряд представлен мультипликативной моделью:

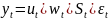
Так как ряд представляет месячные данные, то вычисляются месячные сезонные индексы: S₁, S₂, …, S₁₂, сумма которых S₁+S₂+…+S₁₂=1200%.

Процедура вычисления сезонных индексов состоит из нескольких шагов:

1. Выделяются тренд и циклическая составляющая при помощи процедуры центрированного скользящего среднего по 12 точкам.

2. Вычисляются сезонная и остаточная составляющие в процентах делением исходных данных на значение тренда и циклической составляющей, полученных на шаге 1:

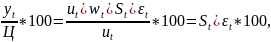
• где Ц – центрированное скользящее среднее.

3. Вычисляются средние результаты шага 2 для каждого месяца. При этом минимальные и максимальные значения в совокупностях месячных данных отбрасываются.

4. Определяется корректирующий коэффициент:

.

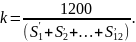
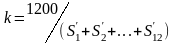5. Определяются скорректированные сезонные индексы: , i=1,2,…,12, сумма которых равна 1200%.

Предположим, что исходный ряд представлен аддитивной моделью:

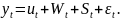
В таком случае метод используется следующим образом:

1. После выделения тренда и циклической составляющей вычитают эти компоненты из исходных данных:

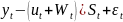
2.Сумма сезонных индексов для аддитивной модели должна быть равна нулю, поэтому корректирующий коэффициент вычисляется по формуле:

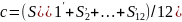
3. Вычисляют скорректированные сезонные индексы: 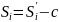, i=1,2,…,12.

Сезонные индексы для мультипликативной и аддитивной моделей приведены в таблице:

Таблица 3. Сезонные индексы

Сезонная составляющая	Мультипликативная модель, %	Аддитивная модель, тыс.
S1	108	890
S2	166	7674
S3	93	–795
S4	77	–2488
S5	80	–2268
S6	55	–5140
S7	59	–4762
S8	172	8347
S9	88	–1443
S10	61	–4762
S11	76	–2882
S12	163	7629