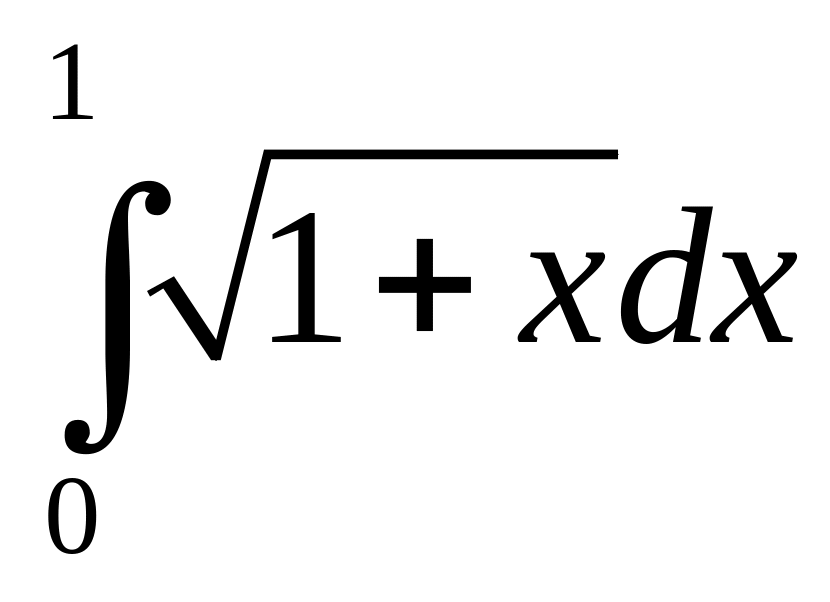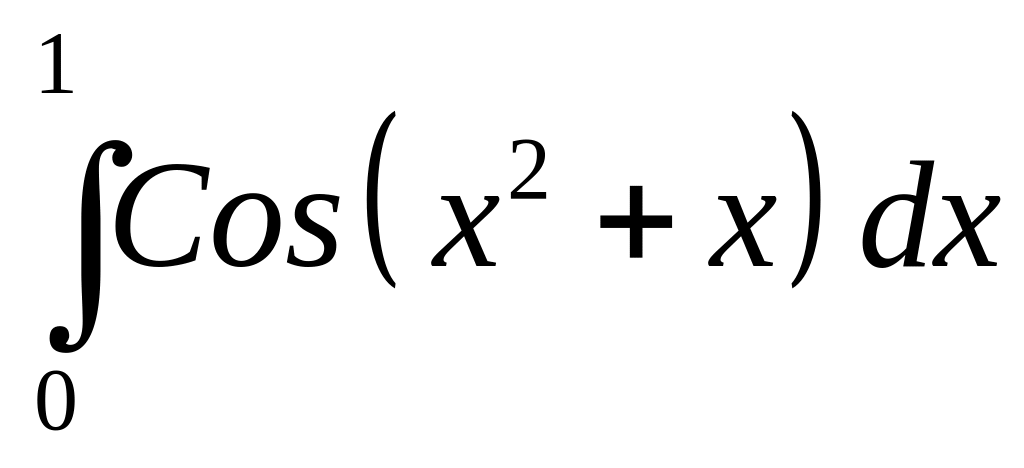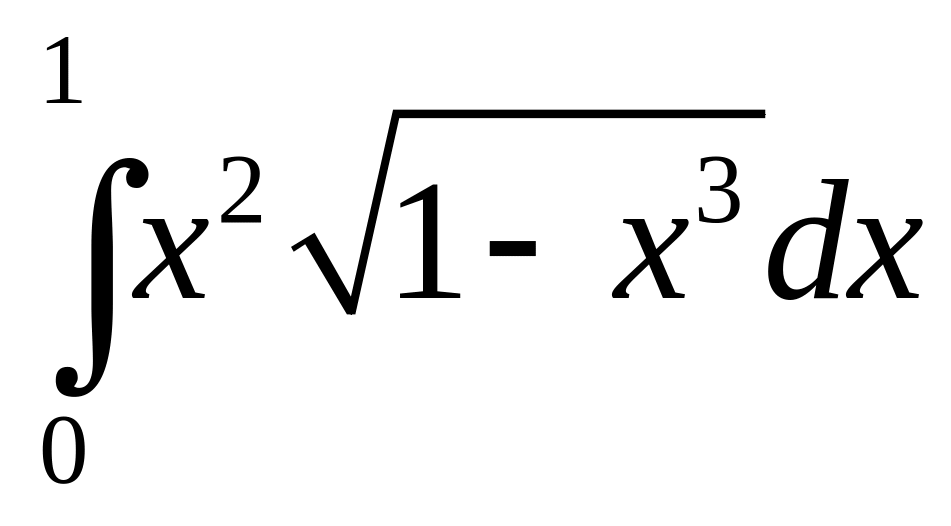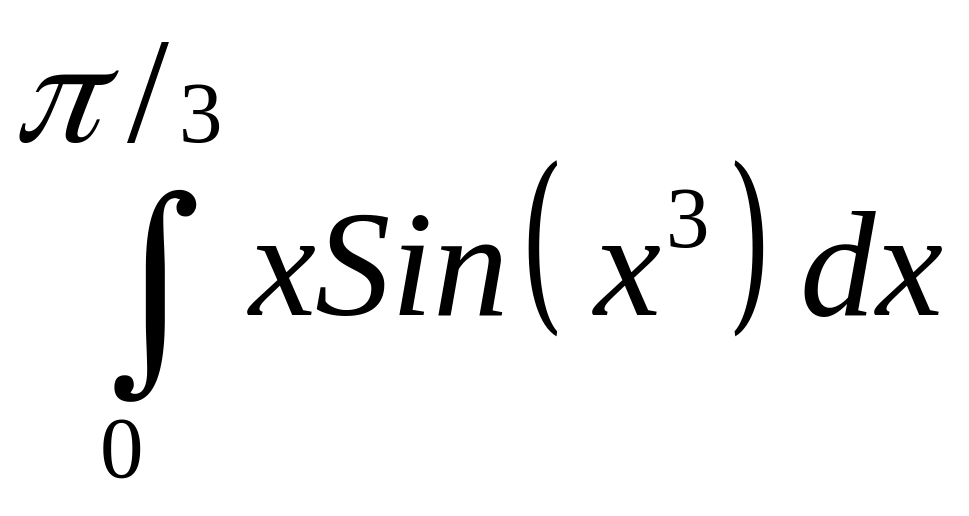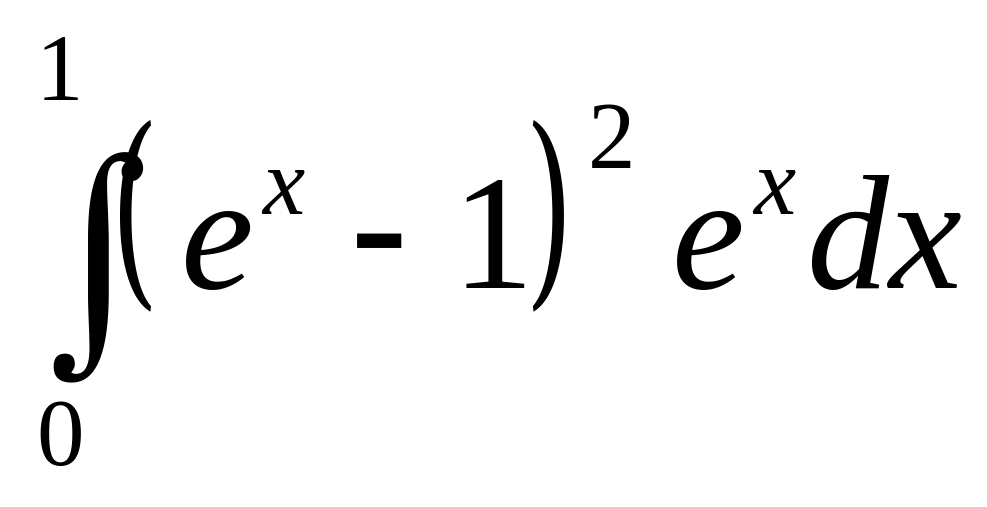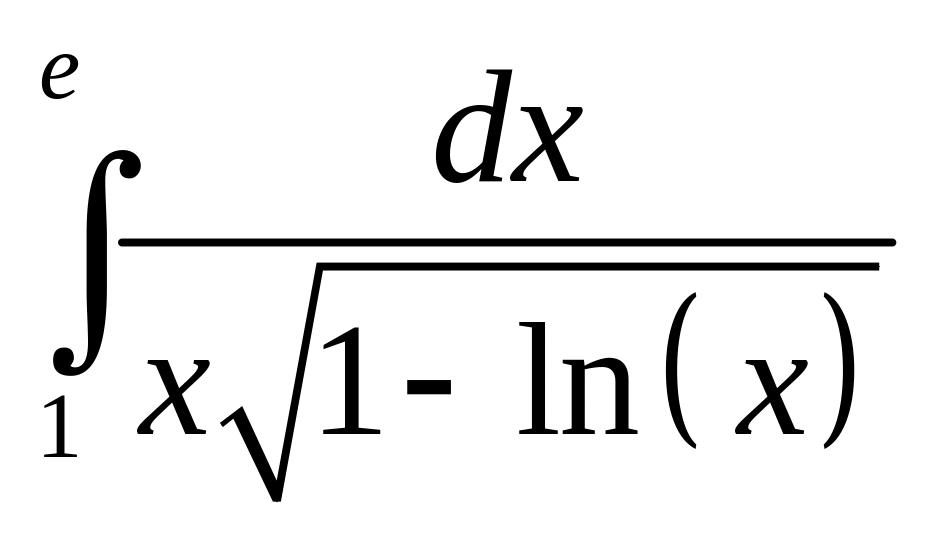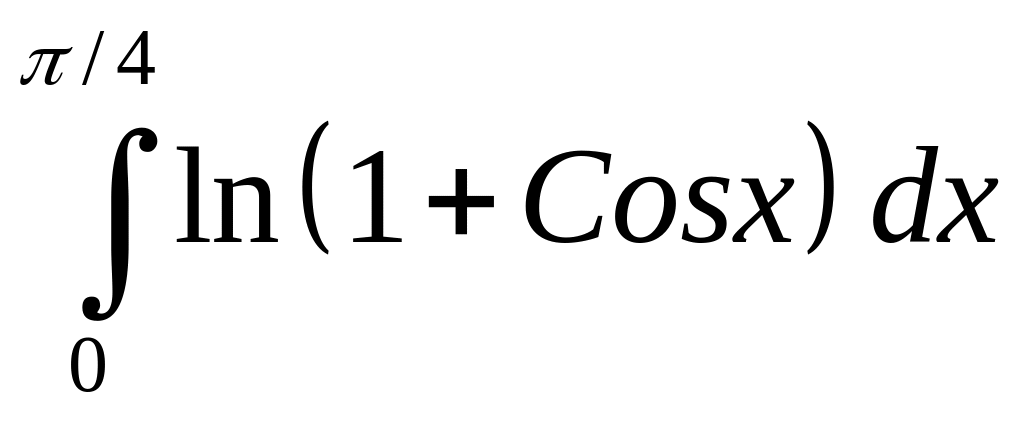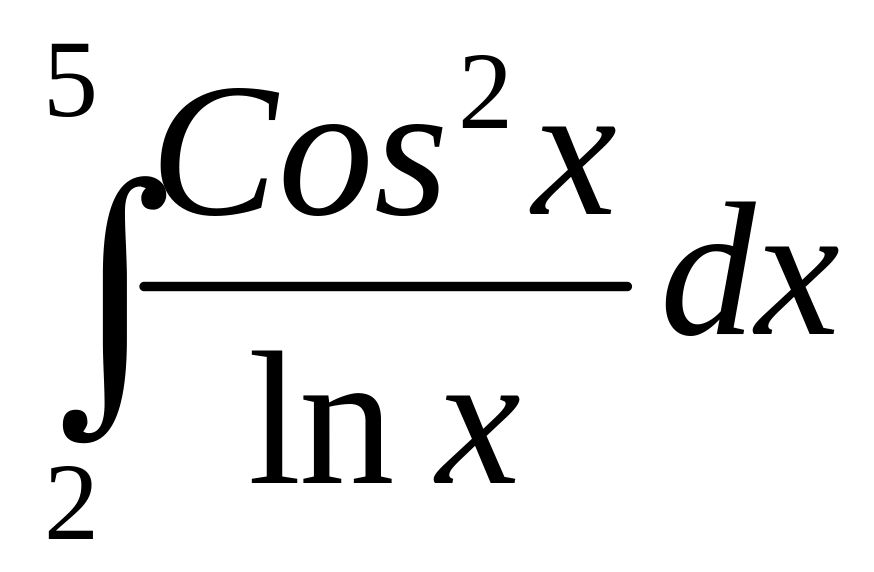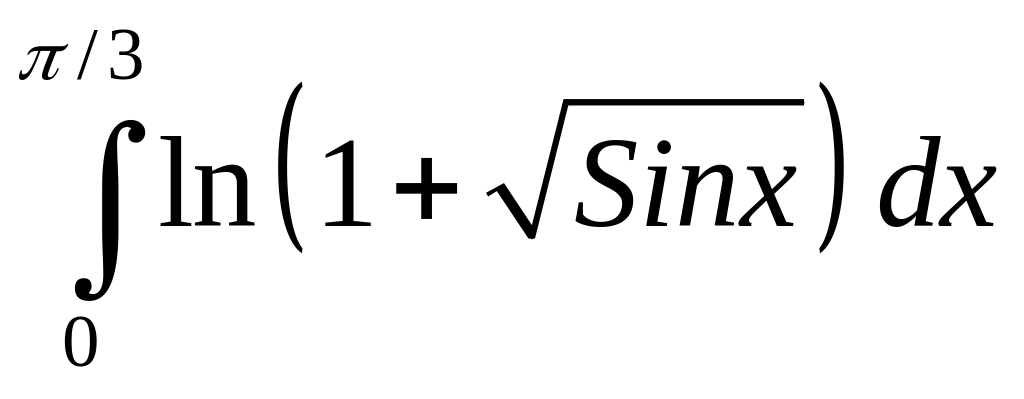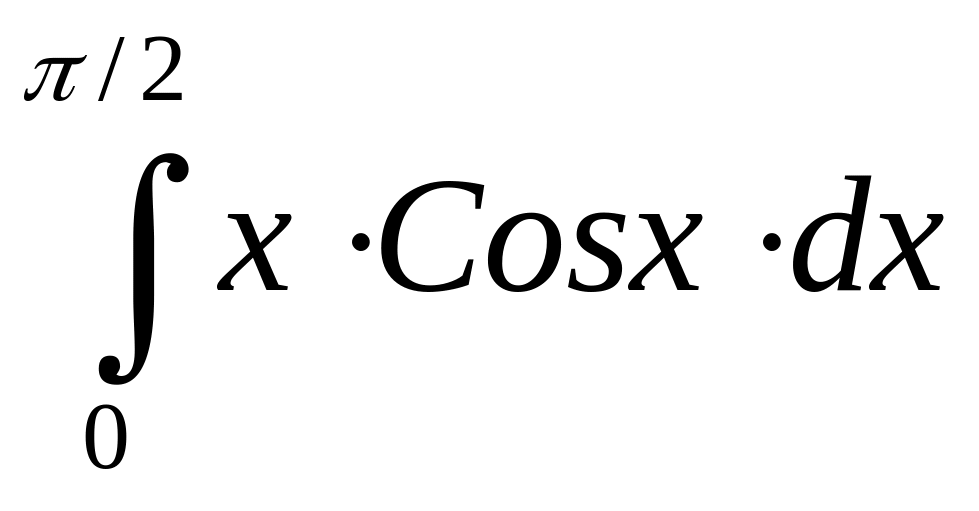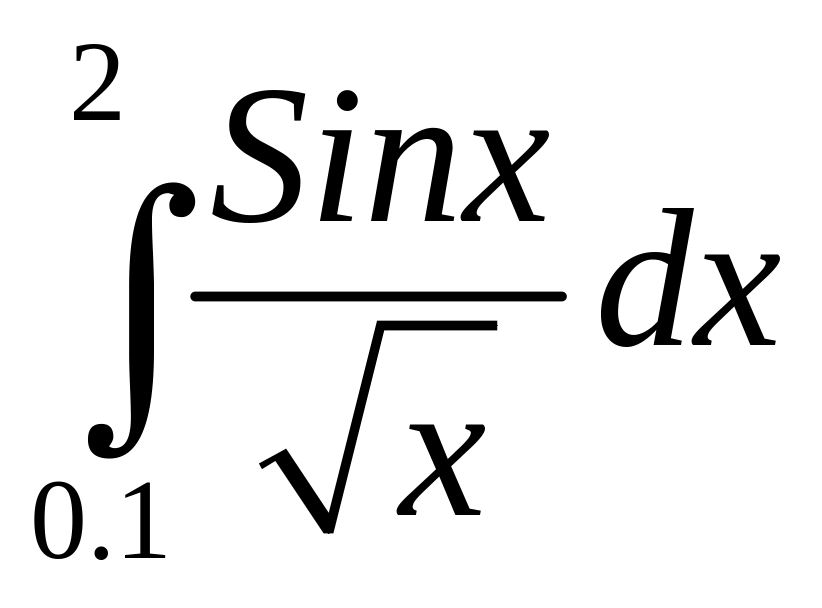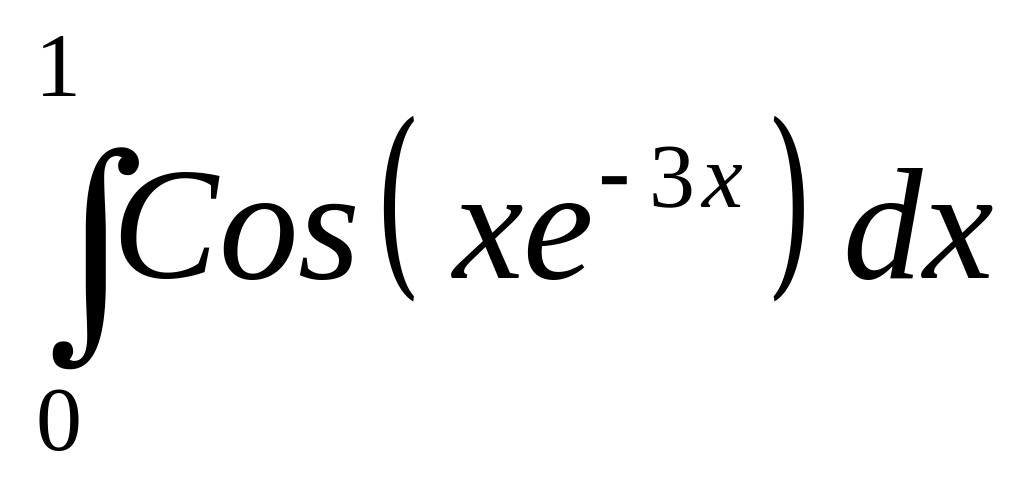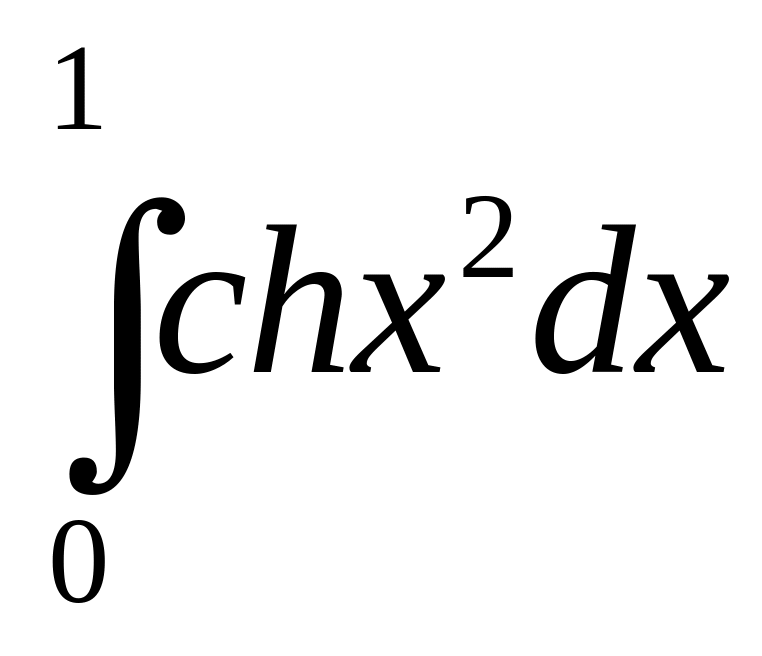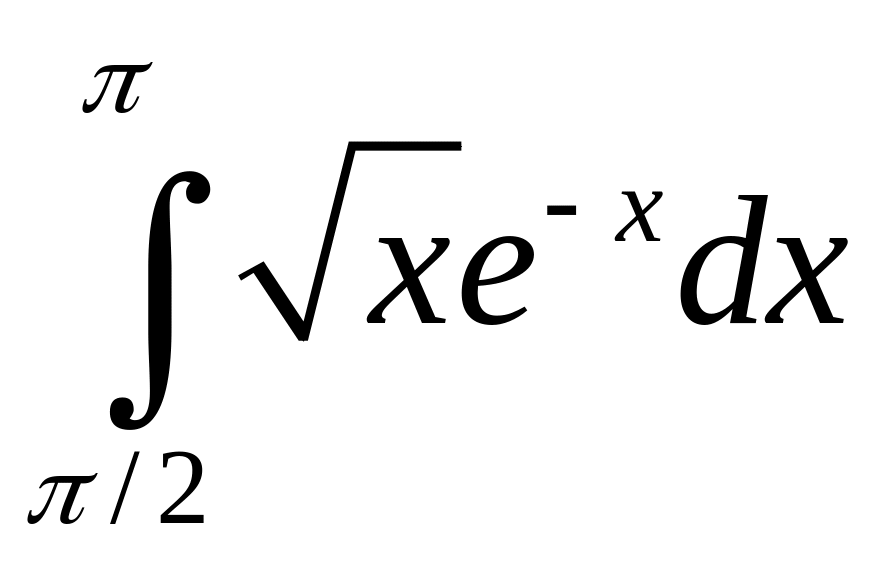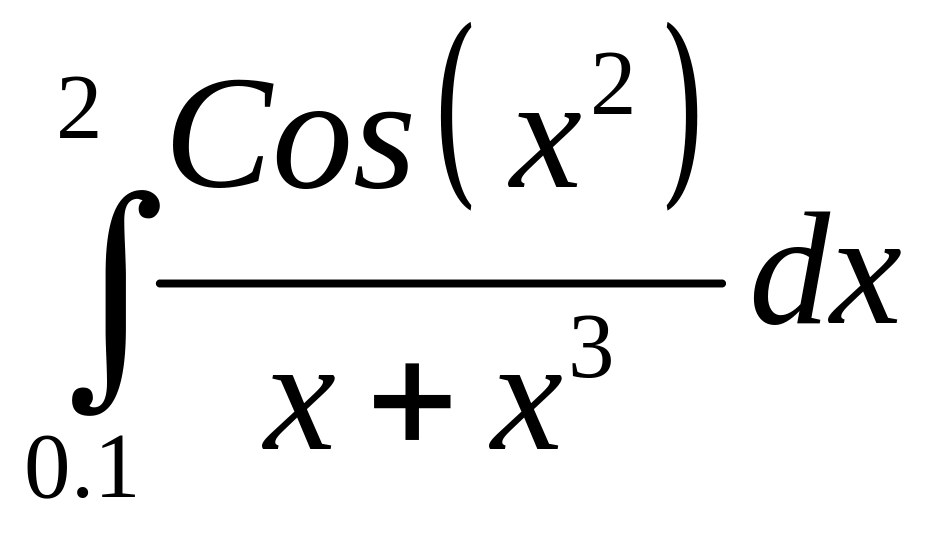2 Варианты контрольных заданий
Таблица 4
Вариант |
|
|
|
|
|
|
|
|
a |
b |
c |
1 |
0.2 |
0.4 |
0.6 |
0.8 |
12.2 |
8.7 |
4.6 |
6.7 |
0.33 |
0.48 |
0.7 |
2 |
1.0 |
1.5 |
2.0 |
2.5 |
0.52 |
0.31 |
0.38 |
0.89 |
1.3 |
1.7 |
2.2 |
3 |
0.0 |
0.1 |
0.2 |
0.3 |
0.0 |
1.45 |
18.3 |
17.6 |
0.05 |
0.18 |
0.22 |
4 |
0 |
2 |
4 |
6 |
-2.5 |
0.17 |
2.5 |
0.3 |
0.5 |
2.5 |
5.5 |
5 |
0.1 |
0.3 |
0.5 |
0.7 |
23.4 |
17.8 |
0.4 |
8.9 |
0.25 |
0.35 |
0.6 |
6 |
1 |
2 |
3 |
4 |
0.06 |
0.11 |
1.78 |
0.09 |
1.3 |
2.5 |
3.8 |
7 |
0.5 |
1.0 |
1.5 |
2.0 |
4.5 |
3.7 |
1.8 |
1.1 |
0.76 |
1.3 |
1.8 |
8 |
0.0 |
0.3 |
0.6 |
0.9 |
0.0 |
12.3 |
13.1 |
12.2 |
0.25 |
0.4 |
0.7 |
9 |
1.2 |
1.4 |
1.6 |
1.8 |
3.5 |
1.3 |
1.1 |
2.9 |
1.25 |
1.55 |
1.7 |
10 |
0.0 |
2.5 |
5.0 |
7.5 |
0.01 |
0.27 |
0.89 |
0.56 |
1.5 |
3.8 |
6.1 |
11 |
0.2 |
0.4 |
0.6 |
0.8 |
2.2 |
0.87 |
0.46 |
0.67 |
0.3 |
0.41 |
0.72 |
12 |
1.0 |
1.5 |
2.0 |
2.5 |
0.43 |
0.28 |
0.16 |
0.76 |
1.45 |
1.68 |
2.1 |
13 |
0.0 |
0.1 |
0.2 |
0.3 |
0.22 |
1.57 |
12.6 |
14.1 |
0.04 |
0.16 |
0.27 |
14 |
0 |
2 |
4 |
6 |
0.2 |
0.76 |
1.6 |
0.9 |
1.2 |
2.3 |
5.1 |
15 |
0.1 |
0.3 |
0.5 |
0.7 |
13.3 |
7.4 |
1.2 |
3.9 |
0.22 |
0.32 |
0.62 |
16 |
1 |
2 |
3 |
4 |
0.2 |
1.2 |
4.7 |
0.8 |
1.4 |
2.6 |
3.2 |
17 |
0.5 |
1.0 |
1.5 |
2.0 |
3.2 |
4.5 |
2.6 |
1.4 |
0.76 |
1.2 |
1.6 |
18 |
0.0 |
0.3 |
0.6 |
0.9 |
0.3 |
2.3 |
3.6 |
2.7 |
0.22 |
0.45 |
0.8 |
19 |
1.3 |
1.6 |
1.9 |
2.2 |
1.4 |
0.7 |
2.6 |
1.6 |
1.5 |
1.8 |
2.0 |
20 |
0.0 |
2.4 |
4.8 |
7.2 |
1.06 |
0.01 |
-0.2 |
0.06 |
1.0 |
3.0 |
5.0 |
Таблица 5
Вариант |
Функция |
Вариант |
Функция |
1 |
|
11 |
|
2 |
|
12 |
|
3 |
|
13 |
|
4 |
|
14 |
|
5 |
|
15 |
|
6 |
|
16 |
|
7 |
|
17 |
|
8 |
|
18 |
|
9 |
|
19 |
|
10 |
|
20 |
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Таблица 3
№ |
Интеграл |
e |
Метод |
№ |
Интеграл |
e |
Метод |
1 |
|
10-6 |
средних прямоугольников |
11 |
|
10-6 |
трапеций |
2 |
|
10-5 |
трапеций |
12 |
|
10-8 |
Симпсона |
3 |
|
10-8 |
Симпсона |
13 |
|
10-6 |
средних прямоугольников |
4 |
|
10-5 |
средних прямоугольников |
14 |
|
10-5 |
трапеций |
5 |
|
10-8 |
трапеций |
15 |
|
10-8 |
Симпсона |
6 |
|
10-6 |
Симпсона |
16 |
|
10-5 |
средних прямоугольников |
7 |
|
10-5 |
средних прямоугольников |
17 |
|
10-8 |
трапеций |
8 |
|
10-8 |
трапеций |
18 |
|
10-6 |
Симпсона |
9 |
|
10-8 |
Симпсона |
19 |
|
10-5 |
средних прямоугольников |
10 |
|
10-5 |
средних прямоугольников |
20 |
|
10-8 |
трапеций |
