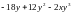7
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ
образовательное учреждение
высшего образования
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
__________________________________________________________________
Кафедра вычислительной техники

ОТЧЁТ
по лабораторной работе №7
«Численное решение обыкновенных дифференциальных уравнений»
по дисциплине: «Вычислительная математика»
Выполнили: Проверил:
Студенты гр. АВТ-341, АВТФ
Калмыкова В. С. Шелудько В. И.
Кардаполова В. С.
«28» апреля 2025 г. «28» апреля 2025 г.
_________________ _________________
(подпись) (подпись)
Новосибирск 2025
Цель работы: На основе заданного дифференциального уравнения приобрести опыт, практические навыки численного решения ОДУ и исследования на основе вычислительных экспериментов основных свойств вычислительных процессов и результатов применения численных методов.
Задание.
Задано одно ОДУ 1-го порядка y’ = f(x, y) с известной функцией f(x, y) . Найти численное решение задачи Коши для этого уравнения на отрезке 0 ≤ x ≤ 1, при y(0) = 1 с помощью системы MathCad, используя три разных метода:
Метод высокого порядка (Рунге-Кутта);
Метод Эйлера;
Неявный метод Эйлера.
48 |
|
Метод Высокого порядка
Методы высокого порядка — это численные методы, которые обеспечивают высокую точность при вычислении производных или интегралов, используя большее количество данных или более сложные аппроксимации



Метод Эйлера
Метод Эйлера — это один из самых простых и широко используемых численных методов для решения обыкновенных дифференциальных уравнений (ОДУ). Он основан на идее аппроксимации производной с помощью конечных разностей.




Неявный метод Эйлера
Неявный метод Эйлера — это численный метод для решения обыкновенных дифференциальных уравнений (ОДУ), который является более устойчивым по сравнению с явным методом Эйлера, особенно для жестких уравнений. В отличие от явного метода, неявный метод использует значения функции в следующем шаге, что требует решения нелинейных уравнений на каждом шаге.





Вывод: Явный метод Эйлера подходит для простых задач, неявный метод — для жестких уравнений, а методы высокого порядка обеспечивают высокую точность и устойчивость для большинства случаев.