Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМК6

.pdf

Скачиваний:

145

Добавлен:

17.03.2015

Размер:

1.57 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Решим эту задачу по следующей схеме:

разобьем

отрезок

[a, b]

на

частей

точками

a = x0 < x1 <...< xi < ... < xn = b ;

выберем в каждом из частичных отрезков [xi−1, xi ] произвольную точку ξi и вычислим значение функции f (ξi ) в этой точке;

2	найдем произведение f (ξi ) xi , где	xi = xi − xi−1 ;
3	составим сумму
	n	xi .
	Sn = ∑f (ξi )	xi .	(1.52)
	i=1
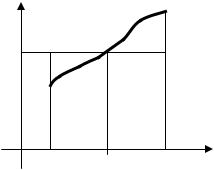
	С геометрической позиции эта	сумма равна	сумме площадей

прямоугольников (рис.1.2), площадь которых приближенно равна искомой площади криволинейной трапеции. Очевидно, что точность этой формулы зависит как от числа точек деления отрезка [a, b] на элементарные части, так и от выбора точек ξi на этих частях;

4 увеличивая число точек деления [a, b] на элементарные части, можно улучшить точность формулы (1.52).

По этой схеме можно приближенно вычислить длину дуги кривой, объем тела вращения, работу, пройденный путь, момент инерции и так далее.

1.9 ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Пусть на отрезке [a, b] задана непрерывная функция y = f (x) . 1 Разделим [a, b] на n частей произвольными точками:

a = x0 < x1 < x2 <...< xi < ... < xn−1 < xn = b .

2На каждом элементарном отрезке [xi−1, xi ] выберем произвольную точку ξi и вычислим значение функции f (ξi ) в этой точке.

3 Вычислим f (ξi ) xi , для всех i =1, 2, ..., n , где xi = xi − xi−1 .

Составим сумму Sn = ∑f (ξi ) xi (1.53)

i=1

Эту сумму назовем интегральной суммой для f (x) на [a, b].

f (x)

и от

4 Обозначим через λ длину наибольшего частичного отрезка для данного разбиения, то есть λ = max xi и продолжим процесс разбиения [a, b] на элементарные отрезки так, чтобы λ → 0.

ОПРЕДЕЛЕНИЕ 1.5 Если существует конечный предел интегральной суммы (1.53) при λ → 0, не зависящий ни от способа разбиения [a, b] на

элементарные отрезки,	ни от выбора точек ξi на этих отрезках, то этот
предел называют определенным интегралом от функции f (x)		на [a, b] и
обозначают следующим образом:
b	n
∫ f (x)dx = lim ∑ f (ξ) xi ,		(1.54)
a	λ→0 i=1

где числа a и b называют соответственно нижним и верхним пределами

интегрирования; [a, b]	промежутком интегрирования; f (x)
подынтегральной функцией; x	переменной интегрирования.

Из решения задачи о площади криволинейной трапеции и определения определенного интеграла следует геометрический смысл определенного интеграла как площади криволинейной трапеции:

b
S = ∫f (x)dx , где f (x) ≥ 0 на [a, b]	(1.55)

Из определения определенного интеграла следует, что величина интеграла (1.54) зависит только от подынтегральной функции f (x) пределов интегрирования a и b. Следовательно, если заданы функция

и числа a и b, то интеграл определяется однозначно. Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения переменной интегрирования, т.е.

b	b	b
∫f (x)dx = ∫f (t)dt = ∫f (ξ)dξ			(1.56)
a	a	a

Примем без доказательства теорему существования определенного интеграла.

Теорема 1.8 Если функция f (x)	непрерывна на отрезке [a, b], то
b	f (x) называется интегрируемой
∫f (x)dx существует. В этом случае	f (x) называется интегрируемой
a
функцией на этом отрезке.

1.10 СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

10		b
10		∫dx = b −a			(1.57)
		a
	Доказательство. По определению определенного интеграла имеем
	b	n	xi = lim(b −a) = b −a
	∫dx = lim ∑		xi = lim(b −a) = b −a
	a	λ→0 i=1	λ→0
20	Для любых чисел a и b выполняется равенство
	b		a
	∫f (x)dx = −∫f (x)dx				(1.58)
	a		b
(свойство 20 доказать самостоятельно).
30	Если функции y = f (x) и y = g(x) интегрируемы на отрезке [a, b], то
	b		b	b
	∫[f (x) +g(x)]dx = ∫f (x)dx + ∫g(x)dx				(1.59)
	a		a	a

Доказательство. По определению определенного интеграла и свойству предела суммы получим

	b	[f (x) + g(x)]dx = lim			n		xi =
	∫				∑[f (ξ) + g(ξ)]
	a			λ→0 i=1
	n		xi + lim	n		b	b
= lim	∑f (ξi )			∑g(ξi )		xi = ∫f (x)dx + ∫g(x)dx
λ→0 i=1			λ→0 i=1			a	a

Доказательство следующих двух свойств аналогично доказательству 30 Поэтому их примем без доказательства.

40 Если функция y = f (x) интегрируема на отрезке [a, b] и C постоянная, то

b	b
∫Cf (x)dx = C∫f (x)dx ,		(1.60)
a	a

то есть постоянный множитель можно вынести за знак определенного

интеграла.

Замечание 1.1 Свойства 30 −40 можно обобщить на любое конечное число слагаемых функций в подынтегральном выражении. Например, если

y = f1(x),

y = f2 (x), ......... ,

y = fn (x)

интегрируемые функции на отрезке

[a, b]; C1, C2 , ... , Cn

постоянные

числа,

то

функция

y = C1f1(x) +C2f2 (x) + ... +Cnfn (x)

также

интегрируема на отрезке [a, b]; причем справедливо равенство

b∫[C1f1(x) +C2f2 (x) + ... +Cnfn (x)]dx =

= C1 ∫f1(x)dx +C2 ∫f2 (x)dx + ... +Cn ∫fn (x)dx.

Если функция y = f (x) интегрируема на отрезке [a, b], то

∫f (x)dx

≤ ∫

f (x)

y = g(x)

Если

на отрезке [a, b],

где a < b , функции y = f (x)

непрерывны и удовлетворяют условию f (x) ≥ g(x) при x [a, b], то

∫f (x)dx

≥ ∫g(x)dx .

(1.61)

Доказательство.

Используя свойство 30 определенного интеграла и

его определение, имеем

∫f (x)dx − ∫g(x)dx =

∫(f (x) −g(x))dx = lim

∑[f (ξi ) −g(ξi )]

λ→0 i=1

По условию f (ξi ) −g(ξi ) ≥ 0 и

xi > 0 .

[f (ξi ) −g(ξi )] xi ≥ 0. Тогда

Поэтому ∑

i=1

lim

∑[f (ξi ) −g(ξi )] xi ≥ 0 .

λ→0

i=1

Следовательно, ∫(f (x) −g(x))dx ≥ 0 и ∫f (x)dx ≥

∫g(x)dx .

70 Если m и M

наименьшее и наибольшее значения непрерывной

функции на отрезке [a, b] функции y = f (x) , то

m(b −a) ≤ ∫f (x)dx

≤ M(b −a) .

(1.62)

Доказательство. Так как f (x) непрерывна на [a, b], то m ≤ f (x) ≤ M .

На основании свойства 60 имеем следующее двойное неравенство:

b	b	b
∫mdx ≤ ∫f (x)dx ≤ ∫Mdx .
a	a	a
Используя свойства 10	и 40 , имеем

y = f (x)

0	a	b x
		Рис.1.3

b b

∫mdx = m∫dx = m(b −a)

∫Mdx = M∫dx = M(b −a)

Следовательно,

m(b −a) ≤ ∫f (x)dx ≤ M(b −a) .

Если f (x) непрерывна на отрезке [a, b], то свойство 70 имеет следующий геометрический смысл (рис. 1.3). Площадь криволинейной трапеции, опирающейся на отрезок [a, b] и ограниченной сверху графиком функции y = f (x) , не больше площади прямоугольника с высотой M и не меньше площади прямоугольника с высотой m , основаниями которых, служит тот же отрезок [a, b].

80 (Теорема о среднем). Если					y = f (x)	функция,	интегрируемая на
отрезке [a, b], то на этом отрезке найдется такая точка ξ, что
			b
			∫f (x)dx = f (ξ) (b −a) .				(1.63)
			a
Доказательство. Пусть a < b и m и M						наименьшее и наибольшее
значения функции y = f (x) на отрезке [a, b].
Тогда на основании 70 имеем следующее двойное неравенство:
					b
			m(b −a) ≤ ∫f (x)dx ≤ M(b −a) .
					a
Так как b −a > 0 , то m ≤				1	b
					∫f (x)dx ≤ M .
					∫f (x)dx ≤ M .
				b −a a
Пусть μ =		1	b
			∫f (x)dx ;
	b		∫f (x)dx ;
	b	−a a

тогда m ≤ μ ≤ M .

y		y = f (x)		Так как непрерывная на [a, b] функция
		y = f (x)		принимает все свои значения между m и M ,
				принимает все свои значения между m и M ,
f (ξ)				то найдется	такая	точка	ξ [a, b], что
					b
				f (ξ) = μ. Тогда ∫f (x)dx = f (ξ) (b −a)
					a
				Если f (x) ≥ 0 , то		равенство (1.63)
0 a	ξ		b x означает, что		площадь криволинейной
	Рис. 1.4			трапеции	равновелика		площади
				трапеции	равновелика		площади

некоторого прямоугольника, основанием которого служит отрезок [a, b], а высотой f (ξ) (рис. 1.4).

90 Пусть функция y = f (x)		интегрируема на отрезках [a, b], [a, c],
[b, c]. Тогда для любых чисел a, b, c справедливо равенство
b	c	b
∫f (x)dx =	∫f (x)dx + ∫f (x)dx .
a	a	c

(свойство 90 доказать самостоятельно).

1.11 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ ИНТЕГРИРОВАНИЯ

Пусть функция y = f (x)	интегрируема	на	отрезке [a, b]. Выберем
произвольное x [a, b]. Тогда	функция будет	интегрируема и на отрезке
[a, x]. Пусть
	x
Φ(x) = ∫f (t)dt ,			(1.64)
	a
где переменная интегрирования обозначена через t			для того, чтобы отличить ее

от переменного верхнего предела интегрирования. Ясно, что при изменении x

на [a, b] интеграл ∫f (t)dt является функцией от x .

Теорема 1.9 Если функция y = f (x) интегрируема на отрезке [a, b], то функция y = Φ(x), определенная формулой (1.64), непрерывна на этом отрезке.

Доказательство. Функция Φ(x) непрерывна, если lim Φ = 0 .

x→0

Докажем это равенство.

Вычислим приращения функции Φ(x) :

x+x

ΔΦ = Φ(x +

x) −Φ(x) =

∫f (t)dt − ∫f (t)dt =

(1.65)

x+ x

= ∫f (t)dt

∫f (t)dt − ∫f (t)dt =

∫f (t)dt

По теореме о среднем

ΔΦ =

∫f (t)dt = f (ξ) (x +

x −x) = f (ξ)

x ,

(1.66)

где ξ [x, x +

x].

Тогда

lim

ΔΦ = lim f (ξ)

x = 0 ,

x→0

а следовательно, и ограниченная на отрезке [a, b]

так как f (x)

непрерывная,

функция.

[a, b] и

Теорема 1.10 Если функция y = f (x)

непрерывна на отрезке

Φ(x) = ∫f (t)dt , то Φ (x) = f (x) для x [a, b].

′

Доказательство. Согласно равенству (1.66) имеем

x+ x

ΔΦ =

∫ f (t)dt

= f (ξ) x,

где ξ [x, x +

x]. Тогда

= f (ξ) , а

′

= lim

= lim f (ξ)

= lim f (ξ) = f (x) .

Φ (x)

x→0

ξ→x

Следовательно,

Φ(x)

дифференцируема

при

x [a, b],

причем

′

Φ (x) = f (x) .

Следствие

Так

как

′

то

по

определению

первообразной

(x) = f (x) ,

для f (x) на

[a, b].

функция Φ(x) = ∫f (x)dx

является

первообразной

Следовательно, теорема 1.10 одновременно доказывает теорему о существовании первообразной для f (x) , то есть теорему существования неопределенного интеграла ∫f (x)dx .

1.12 ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

Теорема 1.11 Если функция y = f (x) непрерывна на отрезке [a, b], то

b
∫f (x)dx = F(b) −F(a) ,	(1.67)
a

где F(x) любая первообразная для функции f (x) на [a, b].
Доказательство.	Согласно следствию	из теоремы	1.10 функция
x			на [a, b].
Φ(x) = ∫f (t)dt является одной из первообразных для f (x)			на [a, b].	Пусть
a
F(x) любая другая первообразная для f (x) .		Тогда Φ(x) = F(x) +C ,		где C
произвольная постоянная.
	x
Или	∫f (t)dt = F(x) +C .		(1.68)

Вычислим значение C, полагая в равенстве (1.68) x = а.

Тогда ∫f (t)dt = F(a) +C ; следовательно, C = −F(a).

Подставляя найденное значение C в равенство (1.68), получим

∫f (t)dt = F(x) − F(a) .

В частности, при x = b получим ∫F(t)dt = F(b) −F(a).

Возвращаясь к старому обозначению переменной интегрирования x , получим формулу Ньютона - Лейбница

∫f (x)dx = F(x) ab = F(b) −F(a) .

Формула Ньютона - Лейбница открыла практически простой и очень удобный метод вычисления определенных интегралов. Согласно этой формуле достаточно найти любую первообразную для подынтегральной функции и вычислить ее приращение на заданном отрезке [a, b].

Примеры:

= 2 −

=1,5

∫xdx = x

= e −1 ≈1,8

∫exdx = ex

4∫cos x dx = sin x

≈ 0,7

1.13 ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ

Теорема 1.12 Пусть дан определенный интеграл

∫f (x)dx ,

где f (x)

непрерывная функция на отрезке [a, b].

Тогда,

если

функция

x = ϕ(t)

непрерывна вместе

со

своей

производной

′

на отрезке [α, β] и ϕ(α) = a , ϕ(β) = b ,

то

справедлива

ϕ (t)

формула

′

∫f (x)dx = ∫

(1.69)

f [ϕ(t)]ϕ

(t)dt .

Формула (1.69) называется формулой замены переменной в

определенном интеграле.

Доказательство. Пусть

F(x)

первообразная

на

[a, b]

для

подынтегральной функции f (x) . Тогда, применяя формулу Ньютона - Лейбница к интегралам равенства (1.69), получим

b
∫f (x)dx = F(x)	ab = F(b) −F(a) ;	(1.70)

a

β	′	β	= F[ϕ(β)]−F[ϕ(α)]= F(b) −F(a) . (1.71)
	′	β
∫f [ϕ(t)]ϕ (t)dt = F[ϕ(t)]		α
α

Сравнивая правые части равенств (1.70) и (1.71), получим

b	β	′
		′
∫f (x)dx = ∫f (ϕ(t)) ϕ (t)dt .
a	α

Пример 1.27 Вычислить интеграл

R2 − x2 dx .

∫

Решение.

Пусть x = R sin t . Тогда dx = R cosdt .

Найдем новые пределы интегрирования.

Полагая

x = 0

и x = R ,

вычисляем соответствующие значения

t = 0 и t =

π . Тогда по формуле замены

переменной, получим

x2 + y2 = R2

∫ R

2 − x2 dx = ∫ R2 −R 2 sin2 tR cos t dt =

= R2

∫

1−sin2 t cos t dt = R2

∫cos2 tdt

R 2

sin 2t

πR

Рис. 1.5

(1+cos 2t)dt =

∫

t +

Вычисленный интеграл, с геометрической точки зрения, численно равен

площади

круга, ограниченного окружностью x2 + y2 = R2

(рис.1.5).

1.14 ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ В ОПРЕДЕЛЕННОМ

ИНТЕГРАЛЕ

Пусть u = u(x) , v = v(x)

дифференцируемые функции на отрезке [a, b].

Тогда на этом отрезке

′

d[u(x) v(x)] =[u (x) v(x) + u(x)v (x)]dx .

Интегрируя это равенство по промежутку [a, b], получим

∫d[u(x) v(x)]=

∫u′(x) v(x)dx +

∫u(x)v′(x)dx .

По формуле Ньютона - Лейбница b∫d[u v]= u(x) v(x)

ab ;

тогда

′

(1.72)

u(x) v(x)

= ∫v(x)

u (x)dx + ∫u(x) v (x)dx .

Перепишем последнее равенство в следующем виде:

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.20151.66 Mб66УМК.PDF
#
17.03.20152.52 Mб107УМК.PDF
#
17.03.20153.93 Mб93УМК.PDF
#
17.03.20152.61 Mб58УМК.PDF
#
17.03.20151.65 Mб25УМК11.pdf
#
17.03.20151.57 Mб145УМК6.pdf
#
01.04.2025310.27 Кб1УМКД Медицина катастроф.doc
#
01.05.202588.06 Кб0УМП Тексты по специальности БТС, БТН для самос...doc
#
17.03.2015430.08 Кб12УМП . Сб. к.р.2011.doc
#
17.03.2015219.14 Кб80УМП ВРЕМЕНА1.doc
#
06.03.20164.28 Mб46УМП для выполнения КР Наг.маш..docx