Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМК11

.pdf

Скачиваний:

Добавлен:

17.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 175 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Ответ: 2 πi.

ПРИМЕР 1.23. Вычислить интеграл ∫

; L : a)

z −1

=1;

L (z −1)3 (z +1)3

б)

z +1

=1; с)

= R, R ≠1.

Обозначая искомый интеграл через ∫

, имеем (см. формулу (1.128) при

n = 2)

а)

∫=∫

(z +1)3

2 πi

′′

где

−1)3

(1),

L L

функция в замкнутом круге с границей а).

Найдем

′

−3

′

= −3

f (z)= [(z +1)

]

′′

. Отсюда

∫=

πi ;

f (1)=

f (z)=	1	− аналитическая
	(z +1)3

(z +1)−4 , f ′′(z)=12 (z +1)−5 ,

б)

∫=∫

(z −1)3

= πi f

′′

f (z)=

−

аналитическая

(z +1)3

(−1), где

(z −1)3

L L

функция в замкнутом круге с границей б).

′

−3 ′

(z −1)

−4

′′

−5

f (z)= [(z −1)

] = −3

(z)=12 (z −1)

′′

. Отсюда

∫

= −

πi .

f (−1)= −

R <1,

с)

Если

то подынтегральная функция аналитична в замкнутом

круге с границей с). Согласно теореме Коши искомый интеграл равен нулю. Если же R > 2, то рассматриваем трехсвязную область, ограниченную окружностями а), б), с). Здесь подынтегральная функция аналитична, и по теореме Коши

∫

(z −1)3 (z +1)3

(z −1)3 (z

+1)3

(z −1)3

(z +1)3

z−1

z+1

πi −

πi = 0.

Ответ: а)

πi; б) −

πi; с)0.

πz

sin

ПРИМЕР 1.24. Вычислить интеграл ∫

dz .

(z −1)2

(z −3)

z−1

sin

πz

Решение.

∫= ∫

z −3

′

где

(z −1)2

= 2 πi f (1),

• 1

sin

πz

z−1

f (z)=

есть аналитическая функция в замкнутом

z −3

z −1

=1. Ее производная

круге с границей

πcos

πz

(z −3)−sin

πz

f (z)=

′

(z −3)2

2 cos

4 −sin 4

π cos

4 + sin

′

= −

= − 8 (π + 2).

f (1)=

Ответ: −

2 πi (π+ 2).

1.8. КОМПЛЕКСНЫЕ ЧИСЛОВЫЕ РЯДЫ. КОМПЛЕКСНЫЕ ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Понятие сходимости комплексной числовой последовательности (КЧП)

ОПРЕДЕЛЕНИЕ 1.26. Говорят, что КЧП

z1 = x1 + i y1 , z2 = x2	+ i y 2	,K,
K, zn = xn + i yn ,K		(1.130)
K, zn = xn + i yn ,K

сходится к КЧ z0 = A + Bi , если для любого числа ε > 0, в частности, сколь угодно малого номер N = N (ε), такой, что как только n > N (ε), то для всех таких номеров выполняется соотношение

	zn − z0	< ε	(1.131)

По-другому (1.131) можно записать так:
	lim zn = z0 = A + B i, zn → z0 = A + B i .		(1.132)

n→∞

Отметим, что N (ε) находится из решения неравенства (1.131), если z0

является пределом указанной числовой последовательности, и только в этом случае. Геометрическая иллюстрация (1.131) заключается в следующем: какой

бы открытый круг ω(z0 , r) радиуса ε с центром в точке z0 ни выбрать, все

члены (1.130), за исключением конечного числа					ε
членов: z1 , z2 ,K, z N , окажутся в этом открытом					ε
круге.					• z N+p
Теорема 1.10.				z0	• z N+p
Теорема 1.10.				• z N+1	•
lim zn = z0 = A + Bi		,		• z N+1
n→∞	= A, lim yn
lim xn	= A, lim yn	= B .	(1.133)
n→∞	n→∞			Рис. 1.21
И тогда первое равенство из (1.132) в записи				Рис. 1.21


выглядит так:	+ i yn )= lim xn + i lim yn .
lim (xn	+ i yn )= lim xn + i lim yn .				(1.134)
n→∞	n→∞		n→∞
Отметим, что критерий Коши для вещественной действительной после-
довательности имеет место и для КЧП, а именно:

	Критерий Коши. Для того, чтобы КЧП (1.130) сходилась к z0 , необхо-
димо и достаточно, чтобы для любого ε > 0, в частности, сколь угодно малого,
существует		номер	N = N (ε), такой, что имеет	место неравенство
	zn+m − zn	< ε при n > N (ε), m =1,2,K.
	zn+m − zn	< ε при n > N (ε), m =1,2,K.
	Комплексный числовой ряд (КЧР)
	Если члены ряда
		∞	= xn + i yn
		∑ zn , zn	= xn + i yn	(1.135)
		1

– комплексные числа, то он называется комплексным числовым рядом (КЧР).

∞	∞
Ряды ∑ x k ,	∑ yk назовем соответственно вещественной и мнимой ча-
k=1	k=1

стью КЧР (1.135). И здесь имеет место стандартная терминология для рядов

n			n	(x k + i yk )=
Sn = ∑ zk		=	∑
k=1			k=1			(1.136)
	n				n
						−
=	∑x k		+ i		∑yk
k=1				k=1

− n −я частичная сумма ряда (1.135).

ОПРЕДЕЛЕНИЕ 1.27. Говорят, что КЧР (1.135) сходится, если сущест-

вует конечный
lim Sn = S = A + B i, A,B R .			(1.137)
n→∞
Предел, где S = A + Bi называется суммой КЧР и это записывается так:
∞	= z1 + z2	+K+ zn +K.
S = ∑ zk	= z1 + z2	+K+ zn +K.
1

Согласно (1.136) соотношение (1.137) означает следующее:

n	n	(1.138)
A = lim ∑ xk , B = lim ∑ yk .		(1.138)
n→∞ k=1	n→∞ k=1

Таким образом, справедлива

Теорема 1.11. КЧР (1.135) сходится , когда совместно сходятся ее вещественная и мнимая части.

Понятие комплексного функционального ряда (КФР)

ОПРЕДЕЛЕНИЕ 1.28. Если члены ряда – функции комплексного пере-

менного, то такой ряд называется комплексным функциональным рядом

(КФР). Таким образом, КФР имеет вид

∞
∑ un (z)= u1 (z)+ u2 (z)+K+ un (z)+K.				(1.139)
1
ОПРЕДЕЛЕНИЕ 1.29. Говорят, что КФР (1.139) сходится в т. z0 , если
∞
∑ un (z0 )				(1.140)
1
есть сходящийся КЧР.
ОПРЕДЕЛЕНИЕ 1.30. Говорят, что D есть область сходимости КФР
(1.139), если в каждой точке z0 D ряд (1.140) сходится.
Тогда сумма ряда (1.139) есть функция от z, z D и s (z)= lim sn (z).
					n→∞
Абсолютная и условная сходимость КЧР и КФР
Рассмотрим КЧР (1.135) и составим ряд из модулей			zn		его членов:
Рассмотрим КЧР (1.135) и составим ряд из модулей			zn		его членов:
∞
∑	zn	.		(1.141)
1

ОПРЕДЕЛЕНИЕ 1.31. Говорят, что КЧР (1.135) сходится абсолютно, если сходится ряд (1.141).

Теорема 1.12. Ряд (1.135) сходится абсолютно , когда сходятся абсолютно его вещественная и мнимая части, то есть сходятся абсолютно ряды

∞	∞
∑ xk , ∑ yk .		(1.142)
1	1
Доказательство. Необходимость. По условию (1.141) сходится абсолют-
но. Из x n , yn	≤ zn = x n2 + yn2	абсолютная сходимость рядов (1.142),

если применить первую теорему сравнения для знакоположительных рядов, что и надо.

Достаточность. zn = x n2 + yn2 ≤ x n + yn	2 абсолютная сходи-
мость ряда (1.135). Теорема доказана полностью.

ОПРЕДЕЛЕНИЕ 1.32. Говорят, что КФР (1.139) абсолютно сходится в

∞

области D , если сходится ∑ u n (z) для всех z D .

∞

Отметим, что в простейших случаях к ряду ∑ u n (z), составленному из

модулей u n (z), применяем известные признаки сходимости знакоположи-

тельных рядов. Поясним это на примерах.

∞

ПРИМЕР 1.25. Найти область абсолютной сходимости ряда ∑ n e−n z .

	1
Решение.	u n (z) = n e−n z = n en (x+i y) = n en x e−n i y =

= n e−n x .

Применяя признак Даламбера к полученному знакоположительному ряду

с общим членом

n e−n x , имеем

lim

u n+1 (z)

= lim

u n+1 (z)

= lim

n +1 e−(n+1)z

lim

u n (z)

n e−n z

n→∞

Требование

<1 дает x > 0.

Ответ: Re z = x > 0 − правая полуплоскость.

Замечание. Так как при x ≤ 0 lim

n e−n x = +∞, то необходимое усло-

n→∞

вие сходимости lim u n (z)= 0 lim

u n (z)

= 0 исходного ряда не выпол-

n→∞

няется. Итак, при x ≤ 0 исследуемый ряд расходится. Таким образом, область сходимости совпала с областью абсолютной сходимости.

ПРИМЕР

1.26. Найти область

абсолютной

сходимости

ряда

∑∞ (−1)n n −z .

u n (z)

(−1)n n −z

e−(x+i y)ln n

Решение.

e−z ln n

e−x ln n e−i y ln n

= e−x ln n = n −x =

n x

∞

∑

− обобщенный гармонический ряд (ряд Дирихле), который схо-

n x

дится при x >1 и расходится при x ≤1.

Ответ:

Re z = x >1 − правая полуплоскость, определяемая

прямой

x =1.

ПРИМЕР

1.27.

Найти

область

абсолютной

сходимости

ряда

∑ 1 e−n z2 .

∞

n 2

−n (x2 −y2 +2i x y)

−n (x2 −y2 )

Решение.

u n (z)

n 2

en (y2 −x2 )

n 2 en (x2 −y2 )

n 2

(n +1)2

e(n+1)(x2 −y2 ) −1

−2

−x2 +y2

−x2

lim

= lim 1 +

= e

n 2 en (x2 −y2 )

ex2

−y2

n→∞

Требование e−x2 +y2 <1 дает − x 2 + y2

< 0 . И в этой области ряд схо-

дится абсолютно. Если − x 2 + y2

= 0 ,

то

u n (z)

. И в этом случае имеет

n 2

u n (z)

место абсолютная

сходимость.

Если

же

y2 − x 2 > 0 ,

то

lim

= lim

en (y2 − x 2 )

= ∞,

n→+∞

то есть необходимое условие сходимости ряда не вы-

n 2

n→∞

Ответ: y2 − x 2

≤ 0.

полняется.

ПРИМЕР

1.28.

Найти

область

абсолютной

сходимости

ряда

∞

∑

(z −3i)2n

u n (z)

n 2n

(n +1) 2n+1

(z −3i)2n

Решение.

lim

(z −3i)2n+2

−3i

n→∞

n 2n

= 2 lim

n +1

;

<1,

z −3i

2 > 2 − внешность

(z −3i)2

z −3i

−3i

n→∞

круга радиуса

2 с центром в точке 3i .

Если

z −3i

≤ 2 , то

u n (z)

≥ n,

lim

u n (z)

= ∞. И нарушается необ-

n→∞

ходимое условие сходимости ряда.

Ответ: z −3i > 2 − внешность круга радиуса 2 с центром в точке 3i .

ПРИМЕР 1.29. Найти область абсолютной сходимости ряда ∑∞ z −i n .

1 z + i

∞

z −i

Решение. ∑1

члены этого ряда образуют геометрическую

z + i

z −i

прогрессию со знаменателем

q =

<1. В противном случае последний

z + i

ряд будет расходиться. Должно быть

z −i

z +i

x 2 + (y −1)2 < x 2 + (y +1)2 , − 2y < 2y, y > 0.

Ответ

: Jm z = y > 0 − верхняя полуплоскость.

Равномерная сходимость КФР
ОПРЕДЕЛЕНИЕ 1.33. Говорят, что КФР сходится равномерно в области
D , если выполняется условие: для ε > 0 номер N = N (ε), такой, что для
всех n > N (ε) и для всех z D выполняется требование
			sn (z)− s (z)		< ε,		(1.143)
			sn (z)− s (z)		< ε,		(1.143)
где s (z)−			сумма КФР s		(z)= lim sn (z) .
					n→∞
Обратим внимание читателя на то, что равномерная сходимость
предполагает сходимость (1.139) в области D к сумме s (z).
Если ряд (1.139) сходится к сумме s (z) неравномерно, то, решая
неравенство (1.143) по заданному						ε > 0, найдем, что N = N (ε, z),	так как,
например,		для z = z0			и z = z1	соответствующие числовые ряды	(1.140)
разные. Равномерная же сходимость означает, что по выбранному ε N от z не
зависит.
Так же, как и в случае вещественного функционального ряда, имеет место
признак Вейерштрасса и критерий Коши о равномерной сходимости.
Признак Вейерштрасса. Если для z D имеет место неравенство
∞			un (z)	≤ cn ,	cn ≥ 0		(1.144)
			un (z)	≤ cn ,	cn ≥ 0		(1.144)

и ∑ cn	− сходится, то КФР (1.139) равномерно сходится в области D .
1
Критерий Коши. КФР (1.139) сходится равномерно к своей сумме f (z)
f (z)=	∞
f (z)=	∑ u n (z) в области D , когда для любого ε > 0 N = N(ε), что
	1
для n > N		(ε) справедливо неравенство
			sn+m (z)−sn (z) < ε,				(1.145)

при m =1,2,K, и для произвольного z из D .

Так же, как и в случае вещественных функциональных рядов, справедливы нижеследующие утверждения, доказательства которых –

буквальный	повтор	доказательств	соответствующих		вещественных
функциональных рядов.
Теорема 1.13. Если члены u n (z) ряда (1.139) непрерывны в области D и
ряд сходится равномерно к своей сумме			f (z) f (z)=	∞
ряд сходится равномерно к своей сумме			f (z) f (z)=	∑ u n (z) , то f (z)−
непрерывная функция в области D .				1
непрерывная функция в области D .
Теорема 1.14. Если члены u n (z) ряда (1.139) непрерывны в области D и
ряд сходится равномерно в D , то его можно почленно интегрировать, то есть
∫	∞	∞			(1.146)
∫	∑ un (z) dz = ∑ ∫ un (z)dz ,				(1.146)
L	1	1 L
где L − кусочно-гладкая кривая, лежащая в области D .
Теорема 1.15. (Вейерштрасса). Если члены un (z) КФР
∑∞ un (z)					(1.147)
1
являются аналитическими функциями в области D , а ряд (1.147) сходится

равномерно к своей сумме f (z) в любой замкнутой подобласти								′ области D ,
равномерно к своей сумме f (z) в любой замкнутой подобласти							D	′ области D ,
то
		10 ) f (z)− аналитическая функция в области D ;
20 )			∞
20 )			f (k ) (z)= ∑ u (nk ) (z)− ряд	можно	почленно	дифференцировать
			1
неограниченное число раз;
		30 )ряд ∑∞ u (nk ) (z) сходится равномерно в любой замкнутой подобласти
			1
		′ области D .
	D	′ области D .
			1.9. СТЕПЕННЫЕ КОМПЛЕКСНЫЕ РЯДЫ
		ОПРЕДЕЛЕНИЕ 1.34. КФР вида
			∑∞ cn (z − z0 )n			(1.148)
			0		СКР, где cn = αn + iβn −
называется			степенным комплексным	рядом	СКР, где cn = αn + iβn −
заданные			коэффициенты, z = x + i y − комплексная			переменная (КП),
z0 = x0 + i y0 − заданное КЧ.
		Не теряя общности, вместо (1.148) рассмотрим СКР
			∞
			∑ cn zn .			(1.149)
			0

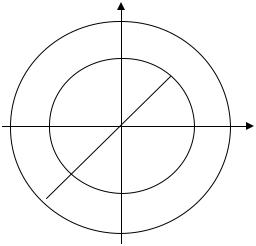
Теорема 1.16. (Абеля). Если степенной ряд (1.149) сходится при z = z0 ≠ 0 , то он абсолютно сходится при всех z , удовлетворяющих условию

(1.150)

Если степенной ряд (1.149) расходится при z = z1

≠ 0 , то он расходится

при всех z , удовлетворяющих неравенству

(1.151)

Геометрическая иллюстрация

теоремы

Абеля

заключается

следующем (см. рис. 1.22): неравенство

(1.150) определяет открытый круг радиуса

≠ 0 c центром в начале координат, в

•

которых ряд (1.149) сходится абсолютно.

Если же

рассмотреть

внешность

круга

• 0

радиуса

≠ 0

(см. (1.151)),

то в этом

множестве точек ряд (1.149) расходится.

z •

Доказательство

теоремы Абеля. Из

сходимости КЧР

∞

zn0

∑cn

(1.152)

Рис. 1.22

z0n

n = 0

lim cn z

lim

= lim

n→∞

lim

n = 0 ,

(1.153)

n→∞

то

есть

cn z0n

−

бесконечно

малая

числовая

последовательность, что

приводит к ее ограниченности:

n ≤ M, M > 0

для всех n .

сn zn0

(1.154)

Теперь,

согласно

(1.154), сделаем оценку:

сn zn0

cn zn0

≤ M

(1.155)

zn0

Если выполняется (1.150), то знакоположительный числовой ряд с общим

членом

сходится,

так

как

его

члены

образуют

геометрическую

прогрессию со знаменателем

<1. Этим первая часть теоремы Абеля

доказана.

Вторая часть теоремы Абеля – следствие первой части. Действительно, если для некоторого z = z2 и z2 > z1 ряд (1.149) сходится, то согласно

первой части теоремы в т. z1 (1.149) есть абсолютно сходящийся ряд. И мы

приходим к противоречию, что завершает доказательство теоремы.

Используя теорему Абеля, можно доказать следующий факт: для каждого степенного ряда (1.149) R ≥ 0, что для всех z < R степенной ряд (1.149) будет сходиться абсолютно. При открытом круге радиуса R с центром в начале координат, для всех z , удовлетворяющих условию z > R , ряд (1.149)

расходится. Это R ≥ 0 принято называть радиусом сходимости степенного ряда.

Если мы рассматриваем общий случай (1.148), то центр окружности будет в т. z0 ≠ 0, отличном от начала координат. В точках самой окружности вопрос остается открытым.

Если взять 0 < r < R (R > 0), то в замкнутом круге z ≤ r степенной ряд (1.149) сходится абсолютно и равномерно. В самом деле, для z = p > 0,

	∞
r < p < R	числовой ряд ∑ cn pn сходится абсолютно. Применяя признак
	0

Вейерштрасса, убеждаемся в справедливости нашего утверждения.

∞

(z +i)n

ПРИМЕР 1.30. Найти радиус сходимости степенного ряда ∑

n n

Решение. Согласно

(1.148)

cn =

z0 = −i ,

u n (z)

z + i

. К

n n

u n (z)

n n

знакоположительному ряду с общим членом

применим радикальный

признак Коши: lim n u n

(z) = lim

z +i = 0 .

Последнее говорит о том,

что

n→∞

для любого z исследуемый ряд сходится абсолютно (R = ∞).

Ответ: R = ∞.

Замечание. Рассматриваемый ряд сходится равномерно в любом

замкнутом	круге		z + i		≤ r ,	так	как	в	этом	круге

u n (z)

z + i

r n

∞ r n

≤

и знакоположительный ряд ∑

сходится.

n n

1 n

Но любая конечная

т. z

может

быть включена в указанный

круг при

подходящем выборе r . Отсюда следует, что в любой ограниченной области исследуемый ряд сходится равномерно.

∞	(z − 2i)n
ПРИМЕР 1.31. Найти радиус сходимости степенного ряда ∑			.
	(n +1)	2n
0

<<< < Предыдущая 1 2 3 45 / 175 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.20151.66 Mб62УМК.PDF
#
17.03.20152.52 Mб102УМК.PDF
#
17.03.20153.93 Mб91УМК.PDF
#
17.03.20151.09 Mб47УМК.PDF
#
17.03.20152.61 Mб46УМК.PDF
#
17.03.20151.65 Mб20УМК11.pdf
#
17.03.20151.57 Mб136УМК6.pdf
#
17.03.2015430.08 Кб10УМП . Сб. к.р.2011.doc
#
17.03.2015219.14 Кб73УМП ВРЕМЕНА1.doc
#
06.03.20164.28 Mб41УМП для выполнения КР Наг.маш..docx
#
07.05.2019478.21 Кб3УМП Интегралы.doc