го уклона к фронтальной или профильной плоскости уровня. Нетрудно видеть, что линейный угол между ЛНУ и ее проекцией
А*В* является равным углу наклона плоскости Б к плоскости Г. По-
этому: измерение двугранного угла между плоскостью общего
положения Б и плоскостью уровня сводится к измерению угла между соответствующей прямой наибольшего уклона плоскости Б и проекцией ЛНУ на выбранную плоскость уровня.
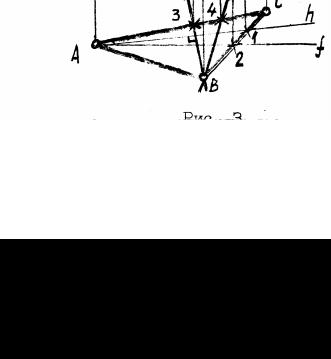
Пример 1. Провести в плоскости Б ( АВС) через точку В прямые наибольшего уклона U1 и U2 к горизонтальной и фронтальной плоскостям (рисунок 2-8). Сначала строим ЛНУ к горизонтальной
|
|
|
плоскости. Для этого в заданной плос- |
|
|
|
|
|
|
|
кости Б проведем горизонталь h- на- |
|
|
|
пример А-1; На предыдущем рисунке 3- |
|
|
|
2 видно, что перпендикулярность к h со- |
|
|
|
храняется и на виде сверху (аналогично |
|
|
|
перпендикулярность к f сохраняется на |
|
|
|
виде спереди; пока без доказательства). |
|
|
|
Учитывая сказанное, проводим ЛНУ |
|
|
|
U1 сначала на виде сверху, а затем (ис- |
|
|
|
пользуя т.2) и на виде спереди. Выде- |
|
|
|
лив на линии наибольшего уклона к го- |
|
|
|
ризонтальной плоскости отрезок (на- |
|
|
|
|
|
|
|
пример B-2), найдем угол его наклона к |
|
|
|
Г плоскости способом прямоугольного |
|
|
|
треугольника. |
|
|
|
Аналогичным образом строим ЛНУ |
|
|
|
к Ф плоскости и находим угол наклона |
|
Рисунок 2-8 |
|
|
|
|
ее (а значит и плоскости) к Ф плоскости. |
|
|
|
|
5. ПРЯМЫЕ ОБЩЕГО ПОЛОЖЕНИЯ
Прямая не параллельная ни одной из плоскостей уровня называется прямой общего положения.
Различают восходящие и нисходящие прямые общего положения.
Восходящая прямая по мере удаления от наблюдателя идет вверх (рисунок 2-9а).
Нисходящая прямая - по мере удаления от наблюдателя такая прямая понижается (рисунок 2-9б).
Реконструируем прямые. Замечаем, что на комплексном чертеже проекции восходящей прямой ориентированы одинаково, а проекции нисходящей имеют различную ориентацию.
Любой отрезок, принадлежащий Рисунок 2-9 таким прямым, на всех проекциях
отображается с искажением.