34. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ, ПЛОСКОСТЕЙ
34.1 Перпендикулярность прямой и плоскости
Если прямая перпендикулярна плоскости, то она перпендикулярна ко всякой прямой этой плоскости (рисунок 13-7а). На комплексном чертеже перпендикулярность будет сохраняться:
• на виде спереди только с фронталью (рисунок 13-7б);
Рисунок 13-7
• на виде сверху только с горизонталью этой плоскости.
Следовательно, если прямая n перпендикулярна плоскости, то на виде сверху она перпендикулярна к горизонтали (n h), а на виде спереди к фронтали (n f) этой плоскости.
Справедливо и обратное утверждение: если проекции пря-
мой перпендикулярны одноимённым проекциям соответствующих линий уровня, то такая .прямая перпендикулярна этой плоскости.
Если прямая перпендикулярна к плоскости частного положения, то прямой угол с вырожденной проекцией сохраняется. Перпендикулярная прямая в этом случае является прямой уровня и, следовательно, проецируется без искажения на том виде, где прямой угол сохраняется.
А
А
Рисунок 13-8
Рассмотрим примеры построения прямой, перпендикулярной к плоскости и плоскости, перпендикулярной к прямой.
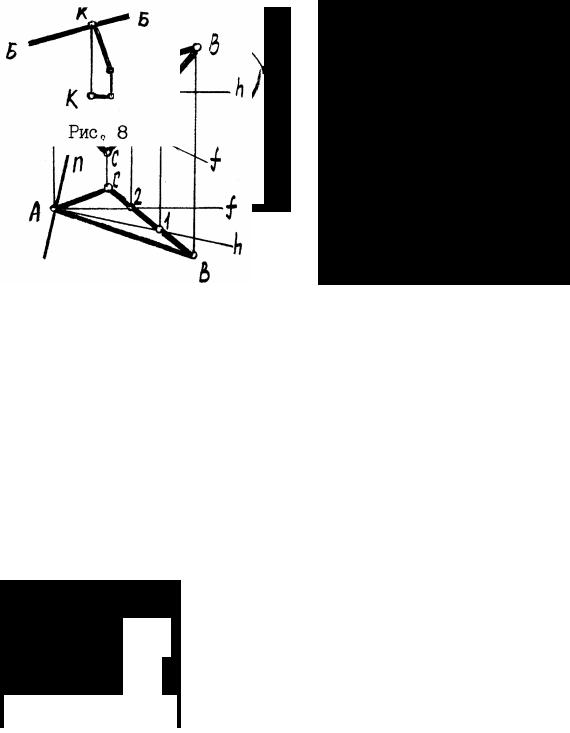
Пример 4. Определить расстояние от т. А до наклонной плоскости Б (рисунок 13-8).
Расстояние от точки до плоскости изме-
ряется перпендикуляром, опущенным из точки на данную плоскость. На виде спереди опускаем перпендикуляр из т. А на плоскость
Б.
Это будет натуральная величина расстояния. На виде сверху прямая АК перпендикулярна линиям связи.
Пример 5. Определить расстояние от т. А до плоскости общего положения Б(a//b), (рисунок
13-9).
Проводим в плоскости Б произвольные горизонталь h и фронталь f.
Строим нормаль к плоскости Б, для чего на виде спереди проводим прямую n перпендикулярно к фронтали f, а на виде сверху перпендикулярно горизонтали h.
Определяем точку пересечения К прямой n с плоскостью Б, для чего строим на плоскости прямую t горизонтальноконкурирующую с прямой n.
Способом прямоугольного треугольника определяем натуральную величину перпендикуляра АК.
Пример 6. Через т.А провести плоскость Д, перпендикулярную прямой общего положения l (рисунок 13-10).
Плоскость Д задаем главными линиями этой плоскости -горизонталью и фронталью. Проводим их через т.А таким образом, чтобы они были перпендикулярны заданной прямой: горизонталь на виде сверху, фронталь - на виде спереди.
Полученная плоскость Д(h∩f) будет перпендикулярна прямой l.
Рисунок 13-10
34.2 Перпендикулярность плоскостей
Две плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой. Но через прямую линию (перпендикуляр) в пространстве можно провести множество плоскостей перпендикулярных данной.
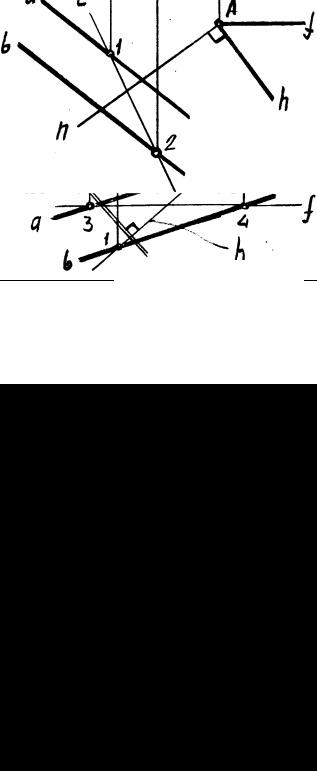
Пример 7. Провести через т.А плоскость Б, перпендикулярную заданной плоскости Д(а//b), (рисунок 13-11).
Сначала проведем через т.А прямую n перпендикулярно плоскости Д, для чего на ней предварительно проводим горизонталь и фронталь.
Затем через т.А проводим произвольную прямую l.
Эти две прямые n и l задают одну из плоскостей перпендикулярных плоскости Д.
Пример 8. Определить, перпендикулярны ли данные плоскости Б(а//b)и Д(f∩h), (рисунок 13-12).
Из точки пересечения горизонтали h и фронтали f проводим прямую n перпендикулярно плоскости Б.
Проверим принадлежность прямой n плоскости Б. Если плоскости перпендику-
|
|
|
лярны, то нормаль n будет |
|
|
|
либо принадлежать, либо бу- |
|
|
|
дет параллельна плоскости Б. |
|
|
|
В нашем случае прямая n |
|
|
|
не принадлежит и не парал- |
|
|
|
лельна этой плоскости (о чем |
|
|
|
можно судить по расположе- |
|
|
|
нию проекций n и t на видах), |
|
|
|
следовательно плоскость Б не |
|
Рисунок 13-12 |
|
|
|
|
перпендикулярна плоскости Д. |
|
|
|
|
|
|
|
|
|
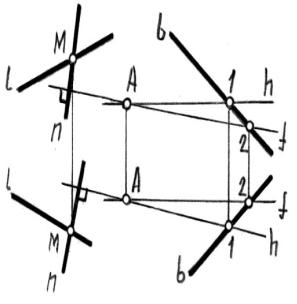
Пример 9. Через прямую l провести плоскость Д перпендикулярно плоскости Б (А, b) (рисунок 13-13).
На прямой l берем произвольную точку М и через неё проводим прямую n перпендикулярно плоскости Б. Пересекающиеся прямые l и n задают искомую плоскость.
Рисунок 13-13