ФОПИ _Чередов_1

Физические основы полученияинформации

ределяется по максимальной разности выходных значений ПИП, полученных в двух циклах градуировки (рис. 4.2г), и обычно выражается в процентах от максимального значения входного сигнала [20]:

Рис. 4.2

Насыщение – это состояние датчика, когда при определенном уровне входного воздействия датчик перестает отвечать приведенной градуировочной характеристике.

Так как в любом средстве измерений сигналы, в том числе и входной сигнал, не могут распространяться с бесконечно большой скоростью, ПИП обладают не только статическими, но и динамическими характеристиками, т. е. параметрами, зависящими от времени. Взаимосвязь между входным воздействием и выходным сигналом ПИП (датчиков) можно описывать в виде линейных дифференциальных уравнений с постоянными коэффициентами, которые в зависимости от конструкции датчиков могут иметь разный порядок. Динамические характеристики СИ можно получить из решения таких уравнений.

К динамическим характеристикам датчиков относятся: операторная чувствительность, комплексная чувствительность, переходная характеристика, ам- плитудно-частотная и фазочастотная характеристики (АЧХ и ФЧХ) и др. Некоторые из этих характеристик определены в п. 1.4.

Если в датчике нет энергонакопительных элементов (конденсаторов, катушек индуктивностей, массы и т. п.), то такой датчик называется датчиком нулевого порядка с передаточной функцией

где А0 – постоянное смещение; S – статическая чувствительность.

Такие датчики относятся к СИ мгновенного действия и для них можно не определять динамические характеристики. На практике в реальных датчиках на

~91 ~

Физические основы полученияинформации

очень высоких частотах чувствительность S уменьшается, что может быть обусловлено наличием упругости, массы, паразитных емкостей и т. д. Поэтому такие датчики называют датчиками квазинулевого порядка. Примером такого датчика может являться реостатный датчик смещения (перемещения).

Датчики, содержащие один энергонакопительный элемент, описываются дифференциальным уравнением первого порядка

Примером датчика первого порядка является терморезистивный датчик, в котором роль энергонакопительного элемента играет теплоемкость. Для описания динамических характеристик данных датчиков широко используются ам- плитудно-частотные и фазочастотные характеристики, граничная частота fСР, на которой выходной сигнал уменьшается на 3 дБ. Эта частота считается предельной рабочей частотой датчика и называется частотой среза. Она характеризует наибольшую или наименьшую частоту внешних воздействий (входной величины), которую датчик может воспринять без искажений [20].

При подаче на вход датчика первого порядка ступенчатого воздействия его переходная характеристика хорошо аппроксимируется экспонентой вида

где Y0 – установившееся значение выходного сигнала; τ – постоянная времени; t

– время.

Постоянная времени τ – это время, в течение которого выходной сигнал датчика достигает уровня, составляющего приблизительно 63 % от установившегося значения при подаче на его вход ступенчатого внешнего воздействия. Постоянная времени является мерой инерционности датчика и в терминах электрических величин находится как τ = C.R. В тепловых терминах под С и R понимаются теплоемкость и тепловое сопротивление.

На практике для установления τ или f датчиков первого порядка можно использовать формулу [20] fСР = 0,159/τ.

Датчики, содержащие два энергонакопительных элемента, описываются дифференциальным уравнением второго порядка

Примером датчика второго порядка является акселерометр, в котором роль энергонакопительных элементов играют масса и пружина.

~92 ~

Физические основы полученияинформации

При подаче на вход датчика второго порядка ступенчатого воздействия на его выходе практически всегда появляются колебания. Любой датчик второго порядка характеризуется собственной (резонансной) частотой, на которой происходит значительное увеличение выходного сигнала. Обычно рабочий диапазон датчиков выбирается либо значительно ниже собственной частоты (на 60 % и более), либо выше ее, кроме тех датчиков, для которых резонансная частота является рабочей. Для датчиков второго порядка необходимо указывать значение собственной частоты и его коэффициент затухания, который может быть определен как отношение большей амплитуды к меньшей амплитуде пары последовательно взятых полуволн колебаний относительно установившегося значения.

Кроме метрологических характеристик при эксплуатации средств измерения важно знать и неметрологические характеристики: показатели надежности, электрическую прочность, сопротивление изоляции, устойчивость к климатическим и механическим воздействиям, время установления рабочего режима, экономичность и др.

4.2. ДИНАМИЧЕСКИЕ МОДЕЛИ ПИП

Для анализа возможных характеристик различных преобразователей, в том числе ПИП, широко используется математическое моделирование, которое бывает статическим и динамическим. Статическое моделирование основано на использовании статических передаточных функций. Одним из способов оценки динамических характеристик является способ, при котором преобразователь (ПИП, датчик) разбивается на отдельные элементы и каждый элемент рассматривается отдельно, а затем математические описания отдельных элементов объединяются в единую модель. В составе динамических моделей обязательно должна входить независимая переменная – время.

Рассмотрим некоторые элементы динамических моделей [20].

4.2.1. Механические элементы

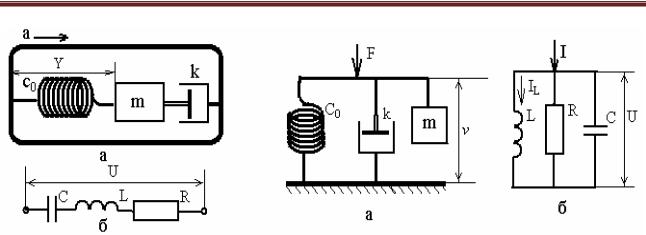
Динамический механический элемент можно представить в виде массы (инерционного компонента), соединенной с пружиной и демпфирующим (успокаивающим) устройством. На рис. 4.3а и 4.4а показаны два возможных варианта механических моделей датчиков силы, давления, ускорения и т. п., в которых масса m удерживается пружиной с коэффициентом жесткости k. Движение этой массы демпфируется устройством успокоения с коэффициентом затухания (успокоения) b.

~93 ~

Физические основы полученияинформации

Для модели, показанной на рис. 4.3а, во время движения на устройство действует ускорение а = d2x /dt2 , а выходной сигнал пропорционален отклонению массы на расстояние Y. Исходя из второго закона Ньютона получим

с учетом ускорения свободного падения уравнение движения будет иметь вид

где х – смещение подвижной части; g – ускорение свободного падения.

Для модели, представленной на рис. 4.4а, при воздействии на систему силы F скорость движения v массы m по отношению к земле может быть определена из равенства

Так как v = dx/dt, получим уравнение движения подвижной части механической системы

Уравнения (4.9) и (4.11) являются дифференциальными уравнениями второго порядка и эквивалентны уравнению (4.7). Для устранения нежелательных колебаний на выходе подобных датчиков регулировкой коэффициента затухания k добиваются состояния критического затухания.

~94 ~

Физические основы полученияинформации

Выходная реакция теплового преобразователя на ступенчатое внешнее воздействие характеризуется тепловой постоянной времени, равной произведению теплоемкости на тепловое сопротивление: τ = RC. Уравнение (4.14) является типичным для тепловых датчиков.

4.2.3. Электрические элементы

Существуют три основных электрических элемента: конденсатор, катушка индуктивности и резистор. Для описания систем (электрических схем), состоящих из электрических элементов, широко используются первый и второй законы Кирхгофа. Примерами подобных систем являются схемы, показанные на рис. 4.3б, рис. 4.4б и рис. 4.5б.

Для электрического контура L –C – R (рис. 4.3б) имеем

Для параллельного электрического контура (рис. 4.4б) можно записать уравнение

Уравнения (4.15) и (4.16) соответствуют линейному дифференциальному уравнению второго порядка (уравнение (4.7)), описывающему систему с двумя энергонакопительными элементами.

Пример системы первого порядка с электрическими элементами показан на рис. 4.5б. Эта система описывается дифференциальным уравнением

Это уравнение системы с одним энергонакопительным элементом.

4.2.4. Электрические аналогии

Приведенные выше соотношения показывают, что механические, тепловые и электрические элементы описываются идентичными математическими соотношениями при надлежащей связи между физическими величинами, характеризующими данную систему. Эту связь обычно называют отношениями эквивалентности, и поведение некоторых неэлектрических физических систем можно описать с помощью электрической аналогии. Это означает, что можно взять механический или тепловой элемент, построить для него эквивалентную электрическую схему и анализировать ее с помощью законов Кирхгофа. В табл. 4.1 приведены сосредоточенные элементы механических, тепловых и

~96 ~

Физические основы полученияинформации

электрических схем совместно с уравнениями, описывающими их поведение

[20].

Электрические аналогии могут использоваться при оценке параметров датчиков, а также промежуточных механических и тепловых элементов между объектом и окружающей средой.

4.3. КЛАССИФИКАЦИЯ ПЕРВИЧНЫХ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ

Одним из важнейших элементов любого прибора, предназначенного для измерения физических величин, является первичный измерительный преобразователь, входной величиной (естественной входной величиной) которого является измеряемая величина. Рассмотрим классификацию первичных измерительных преобразователей (в дальнейшем датчиков). Критерий классификации всегда выбирается в зависимости от цели проведения классификации.

Все ПИП (датчики) можно разделить на две категории: пассивные и активные. Пассивный датчик не нуждается в дополнительном источнике энергии и в ответ на изменение внешнего воздействия на его выходе всегда появляется электрический сигнал. Иногда такие датчики называют генераторными. Примерами пассивных ПИП являются термоэлектрические, пьезоэлектрические преобразователи. Активными являются такие датчики, которые для своей работы требуют внешнюю энергию, называемую сигналом возбуждения. Активные датчики иногда называют параметрическими. Примерами активных датчиков являются терморезистивные, тензорезистивные датчики.

Одним из классификационных признаков, по которому могут быть разделены ПИП, является природа естественного выходного сигнала (параметра). По

~97 ~

Физические основы полученияинформации

этому признаку можно выделить девять групп ПИП: 1) ПИП с электрическими выходными сигналами; 2) ПИП с магнитными выходными сигналами; 3) ПИП с механическими выходными сигналами; 4) ПИП с тепловыми выходными сигналами; 5) ПИП с оптическими выходными сигналами; 6) ПИП с химическими выходными сигналами; 7) ПИП с радиоактивными выходными сигналами; 8) ПИП с пространственными выходными сигналами; 9) ПИП с временными выходными сигналами.

В свою очередь, каждая группа содержит несколько подгрупп, разделяемых по виду выходного сигнала.

Например, ПИП с электрическими выходными сигналами разделяются на ПИП, выходным сигналом которых являются: 1) электрическое сопротивление R; 2) электрическая емкость С; 3) электрический заряд q; 4) ЭДС (разность потенциалов) E (U); 5) электрический ток и др.

Рассмотрим первичные измерительные преобразователи в соответствии с этой классификацией.

4.4. РЕЗИСТИВНЫЕ ПИП

Резистивные измерительные преобразователи (РИП) в настоящее время являются самыми распространенными.

Принцип действия РИП основан на изменении их электрического сопротивления при изменении входной величины.

В общем случае на РИП оказывают влияние различные физические величины: электрические ХЭ; магнитные ХМАГ; механические ХМЕХ; тепловые ХТ; оптические ХОПТ; химические ХХИМ; радиоактивные ХРАД; пространственные ХПР; временные ХВР.

Уравнение преобразования РИП в общем случае имеет вид

Чувствительность РИП к различным по физической природе входным величинам рассчитывается по формуле S = R/ Хi.

При построении РИП стремятся к тому, чтобы изменение сопротивления R происходило под действием одной входной величины (реже двух).

РИП состоит из чувствительного элемента с электродами и выводами и различного рода конструктивных элементов.

Чувствительный элемент (ЧЭ) РИП выполняется из: проводниковых, полупроводниковых и диэлектрических материалов.

Материалом ЧЭ может служить как электрически изотропное вещество, имеющее одинаковое электрическое сопротивление по всем направлениям, так и электрически анизотропное вещество, имеющее в разных направлениях различное сопротивление.

~98 ~

Физические основы полученияинформации

Чувствительные элементы могут быть выполнены: 1) твердыми – в виде различных брусков, трубок, проволок, пленок с определенными размерами и формой сечения; 2) жидкими; 3) газообразными – в виде объема, заключенного в камеру с определенными размерами и конструкцией.

Обычно ЧЭ размещается на базовом элементе – каркасе. Для защиты от внешних влияющих факторов используются защитные элементы в виде чехлов и специальных покрытий, кожухов, оболочек.

Основными характеристиками РИП являются: 1) градуировочная (уравнение преобразования) характеристика R = f(x); 2) чувствительность к входной величине S = dR/dx; 3) начальное значение сопротивления R0 (обычно при Т = 0 или 20 0С); 4) диапазон преобразования; 5) погрешность; 6) постоянная времени.

Рассмотрим наиболее часто применяемые группы резистивных датчиков.

4.4.1. Терморезистивные датчики

Принцип действия терморезистивных ПИП основан на изменении сопротивления проводников, полупроводников и диэлектриков под действием температуры. При изменении температуры проводниковых и полупроводниковых веществ изменяется их удельное сопротивление (терморезистивный эффект). Терморезистивный эффект рассмотрен в п. 3.1.2. Кроме этого, при изменении температуры изменяются размеры образца из этого вещества (материала). Эти факторы обусловливают изменение сопротивления проводниковых и полупроводниковых образцов при изменении их температуры. Если зависимость сопротивления материала от температуры известна и воспроизводима, то ее можно использовать для измерения температуры, переходя от измерения температуры

кизмерению сопротивления.

Втерморезистивных преобразователях в основном используются металлические проводниковые и полупроводниковые материалы. Проводниковые металлические терморезистивные преобразователи иначе называют термометрами сопротивления, а полупроводниковые терморезисторы из поликристаллического материала часто называют термисторами. Материалы терморезистивных ПИП (в дальнейшем терморезисторов) должны обладать: большим значением ТКС; стабильностью ТКС во времени и в диапазоне рабочих температур; большим значением удельного сопротивления; инертностью к воздействию различных сред.

Проводниковые металлические терморезистивные датчики

В общем случае зависимость сопротивления чистых металлов от температуры описывается полиномом n-степени [20]

~99 ~

Физические основы полученияинформации

где RТ – сопротивлениепроводника при температуре Т; R0 – сопротивлениепри определенной эталонной температуре Т0, например Т0 = 273 К (0 0C); 1, 2, 3

... – степенные температурные коэффициенты сопротивления материала;Т = Т – Т0.

В узком диапазоне температур зависимость сопротивления металлических проводников от температуры близка к линейной и для ее описания достаточно использовать первые два члена полинома (4.19).

Чувствительность материалов к температуре Т характеризуется величиной температурного коэффициента электрического сопротивления материала, который в общем случае определяется как ТКС= R= R/ T, [1/K]. Значение ТКС большинства химически чистых металлов в интервале температур 0–100 0С со-

ставляет (3–6,8).10-3 К-1.

В качестве материалов для металлических терморезистивных датчиков чаще всего применяют платину, медь и никель. Проводниковые терморезистивные датчики называют термометрами сопротивления.

Уравнение преобразования медных терморезистивных датчиков в интер-

вале температур от -50 до +180 0С может выражаться линейной зависимостью

где R = 4,26 10-3 К-1 – температурный коэффициент сопротивления меди; R0 – сопротивление при 0 0С; t – температура, 0С.

Чувствительность медного терморезистивного датчика в этом диапазоне находится как S = RR0.

Медные термометры сопротивления применяются в диапазоне температур от -200 до +200 0С. При индивидуальной градуировке их можно использовать до температуры -260 0С.

Недостатком медных терморезисторов является их сильная окисляемость при температурах t > 180 0С, что ограничивает их температурный диапазон.

Уравнение преобразования платиновых терморезисторов в диапазоне температур от 0 до 650 0С определяется выражением

где R0 – cопротивление при 0 0С; 1 = 3,90784 10-3 К-1; 2 = 5,7841.10-7 К-2; t –

температура, 0С.

Чувствительность в этом диапазоне находится как S = R0( 1 + 2t).

В диапазоне температур от 0 до -200 0С зависимость сопротивления платинового терморезистора от температуры имеет вид [15]

~100 ~