Бинарные отношения

Язык бинарных и n-арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. В математике большую роль играют бинарные отношения, т.е. отношения, заданные на декартовом произведении двух множеств .

Бинарные отношения используются для определения каких-либо взаимосвязей, которыми характеризуются пары элементов в

• Пример

, . Отношение

,

• П ример.

Рассмотрим два множества A₁ = [0,1], = [2,4]. Если на плоскости выбрать некоторую декартову систему координат, то прямое произведение A₁×A₂ можно представить как прямоугольник. Исходные множества заданы непрерывными интервалами, в этом случае декартовым произведением является область, ограниченная соответствующим прямоугольником на плоскости.

• Определение

Областью определения бинарного отношения R называется множество

• Определение

Областью значений бинарного отношения R называется множество

• Пример Дано 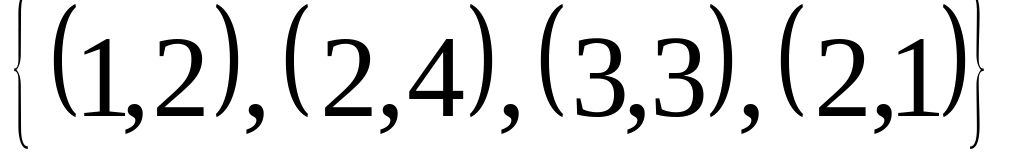- бинарное отношение

Так как бинарные отношения являются множествами, то к ним применимы все понятия, которые вводятся для множеств: понятие равенства, включения, а также операции пересечения, объединения и дополнения

Свойства отношений

• Определение Бинарное отношение  на множестве M называется рефлексивным, если для любого элемента a 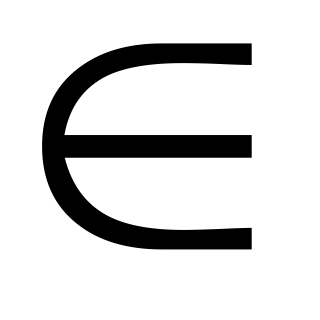M выполняется условие

если a  a для a  M

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.

Для отношения, заданного с помощью матрицы его рефлексивность равносильна тому, что по главной диагонали стоят только символы 1.

• Определение Бинарное отношение  на M называется антирефлексивным,

если ни для одного a M не выполняется a a:

• Определение Бинарное отношение  на множестве M называется симметричным,

если из a  b следует  b a:

• Пример симметричных отношений являются:

• отношение перпендикулярности на множестве прямых;

• отношение касания на множестве окружностей;

• отношение "быть похожим" на множестве людей;

• отношение "иметь одинаковый пол" на множестве животных.

Отношение "x брат y" на множестве всех людей не является симметричным. В то же время отношение "x брат y" на множестве мужчин симметричным является.

В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x.

• Теорема Объединение и пересечение любого семейства симметричных отношений снова являются симметричными отношениями.

• Определение Бинарное отношение на множестве X называется антисимметричным, если для любых различных элементов a и b условия a  b и b  a не выполняются одновременно:

или антисимметричным, если (a b) и (b a)  a = b

• Пример

Отношение "делится" на множестве натуральных чисел является антисимметричным, так как из a b и b a следует, что a = b. Однако на множестве целых чисел отношение "делится" антисимметричным не является.

Отношения "выше", "тяжелее", "старше" антисимметричны на множестве людей. Отношение "быть сестрой" на множестве всех людей антисимметричным не является.

В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.

• Определение Бинарное отношение a на множестве X называется транзитивным, если для любых трех элементов a, b, c X

если (a b) и (b с)  a  c.

Примерами транзитивных отношений служат:

• отношение "делится" на множестве действительных чисел;

• отношение "больше" на множестве действительных чисел;

• отношение "старше" на множестве людей игрушек;

• отношение "иметь одинаковый цвет" на множестве детских игрушек;

д) отношение "быть потомком" на множестве людей.

Отношение "быть похожим" на множестве людей не обладает свойством транзитивности.