Лекция 5 Замкнутые классы функций

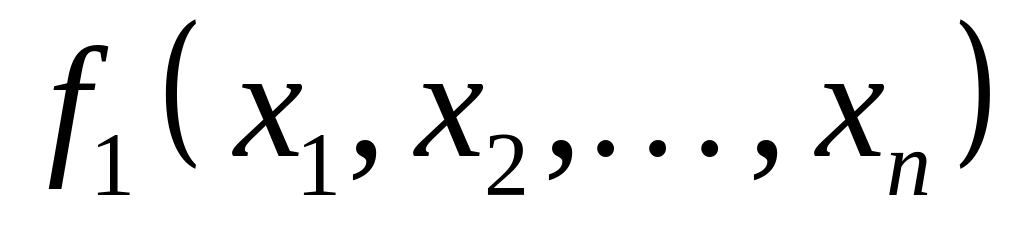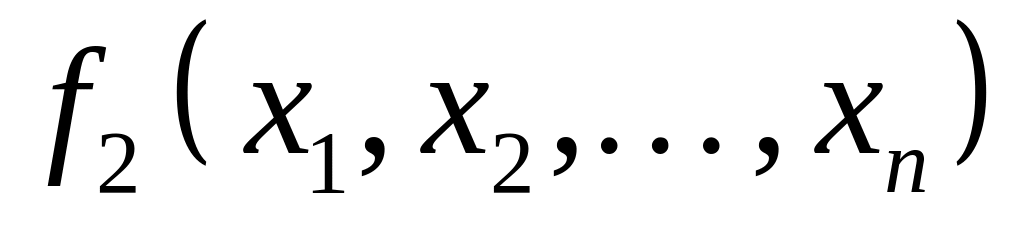• Определение Булевы функции и называются двойственными друг другу, если выполняется соотношение

Двойственными являются функции (табл 1).

Таблица для двойственной функции получается из таблицы инвертированием.

Перечислим классы булевых функций:

1. булевы функции, сохраняющие константу 0 - класс

2. булевы функции, сохраняющие константу 1 - класс

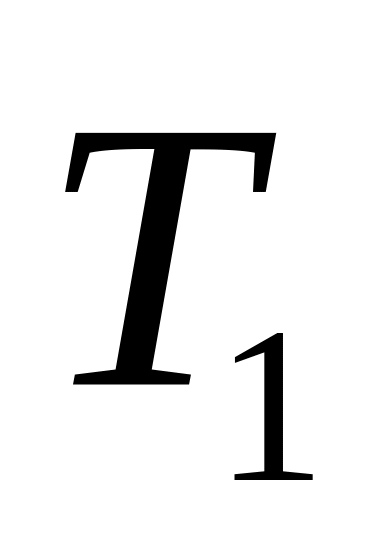
3. самодвойственные булевы функции - класс

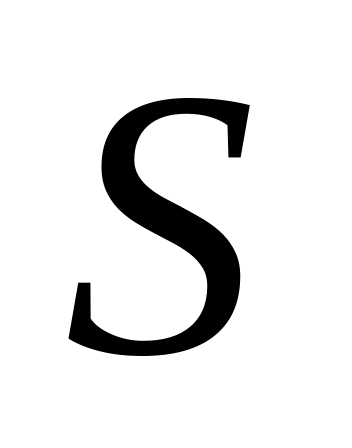
4. монотонные булевы функции - класс

5. линейные булевы функции - класс

Проверка принадлежности булевой функции замкнутым классам 1-4 осуществляется по таблице истинности. Проверка принадлежности булевой функции классу L осуществляется путем построения полинома Жегалкина. – множество всех булевых функций n переменных.

Таблица 1

				запрет по		запрет по
0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1
0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1

Класс

• Определение

К булевым функциям сохраняющим константу 0, относят такие функции , для которых справедливо соотношение .

Класс функций, сохраняющих ноль .

Поскольку таблица истинности для функций, сохраняющих константу 0, в первой строке значений функций содержит 0, то имеется ровно таких функций.

• Пример

примерами булевых функций, сохраняющих константу 0, являются функции (табл 1).

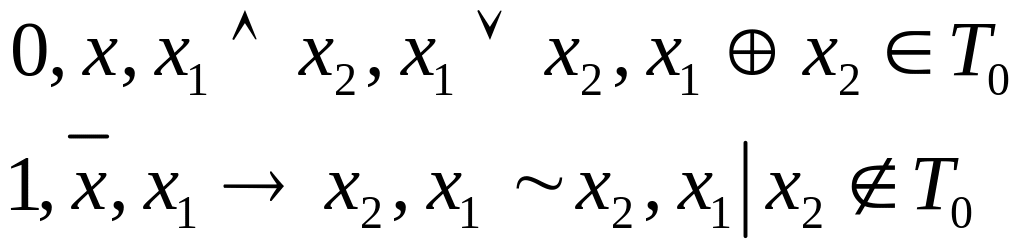
• Теорема Класс замкнут.

Класс

• Определение

К булевым функциям сохраняющим константу 1, относят такие функции , для которых справедливо соотношение

Класс функций, сохраняющих единицу .

Примерами булевых функций, сохраняющих константу 1, являются функции (табл 1).

Поскольку таблица истинности для функций, сохраняющих константу 1, в последней строке значений функций содержит 1, то имеется ровно таких функций.

• Теорема

Класс замкнут.

Класс

• Определение Наборы 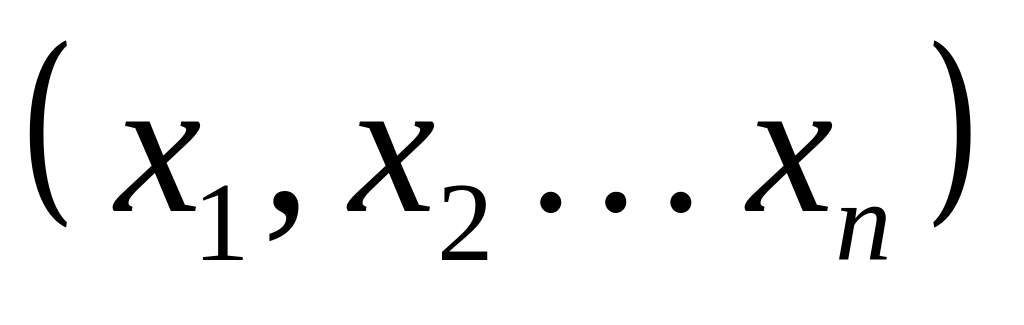и называются противоположными

• Определение Булевы функции и называются двойственными друг другу, если выполняется соотношение

Двойственными являются функции (табл 1).

Таблица для двойственной функции получается из таблицы инвертированием.

• Определение Самодвойственные булевы функции такие булевы функции, которые двойственны по отношению к самим себе, т.е. булева функция называется самодвойственной, если на любых двух противоположных наборах она принимает противоположные значения.

Класс самодвойственных функций

.

• Пример

Самодвойственными являются функции (табл 1).

Из определения самодвойственной функции следует, что она полностью определяется своими значениями на первой половине строк таблицы истинности.

Поэтому число всех самодвойственных булевых функций равно

• Теорема Класс замкнут

Класс

Класс линейных функций L составляют функции, которые представляются полиномом Жегалкина первой степени.

Линейными являются булевы функции (табл.1), ибо

• 

Поскольку линейная функция однозначно определяется заданием коэффициентов то число линейных функций равно .

• Теорема (необходимое условие линейности).

Если функция линейна и не равна некоторой постоянной, то на половине своих наборов она равна 1.

Если в векторе значений функции число 0 и 1 различно, то функция обязательно нелинейна, а если число нулей совпадает с числом единиц, то эта функция может быть линейной, а может быть и нелинейной. В таком случае, чтобы это проверить, нужно выписать для нее многочлен Жегалкина.

• Теорема Класс замкнут

Класс

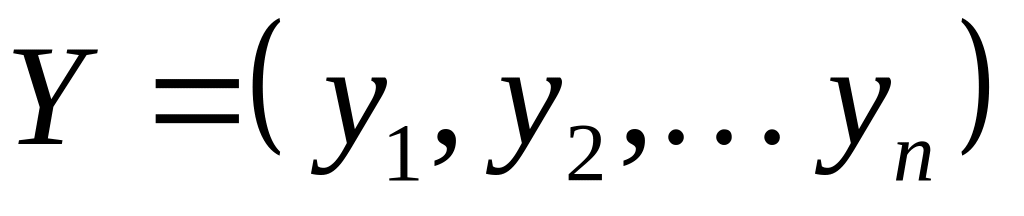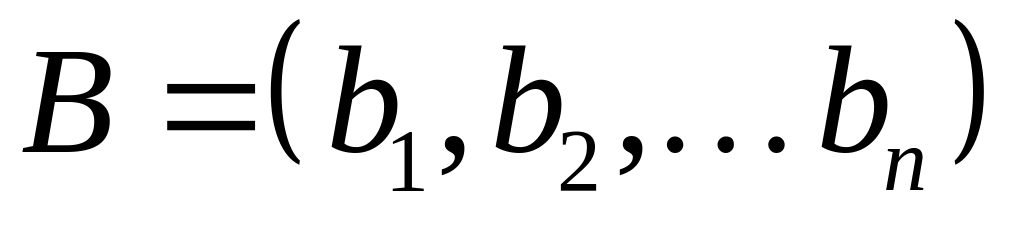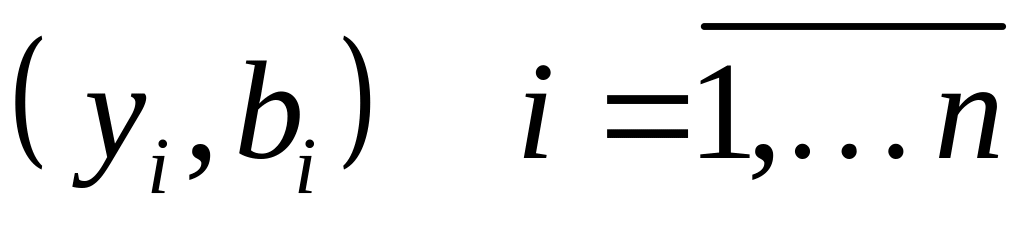• Определение Двоичный набор не меньше двоичного набора , если для каждой пары справедливо соотношение

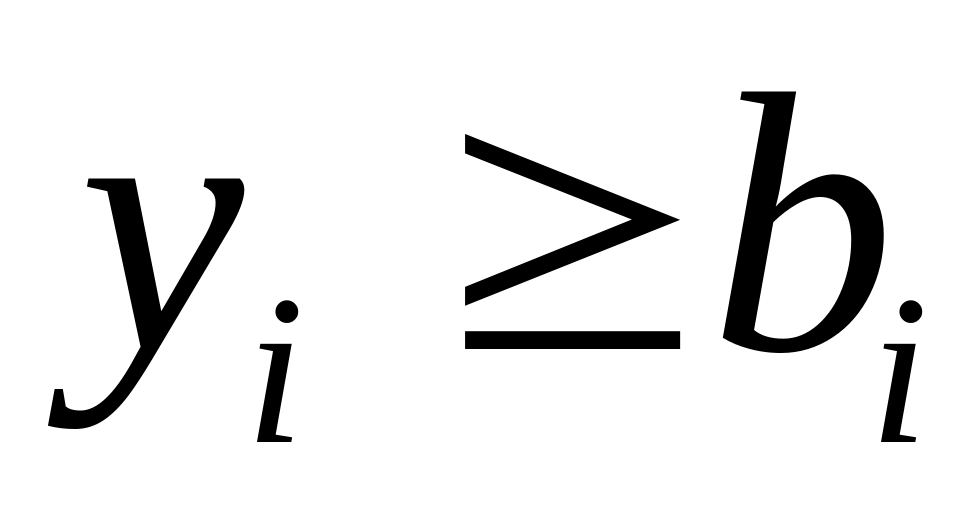
Так, набор 1011 >= 1010. Вместе с тем наборы 1011 и 0100 несравнимы в том смысле, что для них не выполняется ни соотношение , ни .

• Определение Булева функция называется монотонной, если для любых двух наборов и таких, что имеет место неравенство

Класс М монотонных функций. Для двоичных векторов и , где , , вводится следующее отношение частичного порядка. Считается, что , если для всех .

.

• Замечание

Монотонными являются булевы функции (табл. 1).

• Замечание

Функция из табл. 1 не является монотонной, так как

, хотя набор <1,0> меньше, чем набор <1,1>.

У монотонных функций сокращенная ДНФ не содержит отрицаний переменных, то есть все простые импликанты не содержат отрицаний.

• Теорема Класс замкнут.

• . Замечание

Монотонную функцию можно распознать по ее таблице истинности.

Для этого нужно взять все пары строк в таблице, которые отличаются всего в одном столбце (не считая крайнего правого).

Например: 0,0,0,0 и 0,0,0,1; 1,0,0,1 и 1,1,0,1.

Пусть в одной строке в некотором столбце стоит "0", а в другой строке в этом же столбце стоит "1". Нельзя, чтобы в крайнем правом столбце, где записано значение функции было наоборот: "1", а потом "0". Если такая ситуация нигде не встречается, то функция монотонная, и ее можно выразить через и &. Пример монотонной функции: .