6
.docx
![]() ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема:
Сложение гармонических
колебаний
Сопротивление
ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема:
Сложение гармонических
колебаний
Сопротивление ![]() катушка
индуктивности
катушка
индуктивности ![]() и
конденсатор
и
конденсатор ![]() соединены
последовательно и подключены к источнику
переменного напряжения, изменяющегося
по закону
соединены
последовательно и подключены к источнику
переменного напряжения, изменяющегося
по закону ![]() (В).
Установите соответствие между
сопротивлениями различных элементов
цепи и их численными значениями.
1.
Активное сопротивление
2.
Индуктивное сопротивление
3. Емкостное
сопротивление
(В).
Установите соответствие между
сопротивлениями различных элементов
цепи и их численными значениями.
1.
Активное сопротивление
2.
Индуктивное сопротивление
3. Емкостное
сопротивление
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Свободные и вынужденные колебания
Маятник
совершает вынужденные колебания со
слабым коэффициентом затухания
ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Свободные и вынужденные колебания
Маятник
совершает вынужденные колебания со
слабым коэффициентом затухания ![]() ,
которые подчиняются дифференциальному
уравнению
,
которые подчиняются дифференциальному
уравнению 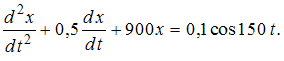 Амплитуда
колебаний будет максимальна, если
частоту вынуждающей силы уменьшить
в _____ раз(-а).
Амплитуда
колебаний будет максимальна, если
частоту вынуждающей силы уменьшить
в _____ раз(-а).
|
|
|
5
| |
Решение:
Дифференциальное
уравнение вынужденных колебаний имеет
вид 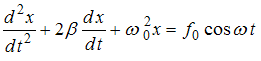 ,
где
,
где ![]() коэффициент
затухания,
коэффициент
затухания, ![]() собственная
круговая частота колебаний;
собственная
круговая частота колебаний; ![]() амплитудное
значение вынуждающей силы, деленное на
массу;
амплитудное
значение вынуждающей силы, деленное на
массу; ![]() частота
вынуждающей силы. При слабом затухании
(коэффициент затухания значительно
меньше собственной частоты колебаний
маятника) амплитуда колебаний будет
максимальна, если частота вынуждающей
силы совпадет с собственной частотой
колебаний маятника (явление резонанса).
Собственная частота колебаний равна:
частота
вынуждающей силы. При слабом затухании
(коэффициент затухания значительно
меньше собственной частоты колебаний
маятника) амплитуда колебаний будет
максимальна, если частота вынуждающей
силы совпадет с собственной частотой
колебаний маятника (явление резонанса).
Собственная частота колебаний равна: ![]() ,
частота вынуждающей силы
,
частота вынуждающей силы ![]() .
Следовательно, частоту вынуждающей
силы необходимо уменьшить в 5 раз.
.
Следовательно, частоту вынуждающей
силы необходимо уменьшить в 5 раз.
![]() ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Энергия волны. Перенос энергии
волной
Показатель
преломления среды, в которой распространяется
электромагнитная волна с напряженностями
электрического и магнитного полей
соответственно
ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Энергия волны. Перенос энергии
волной
Показатель
преломления среды, в которой распространяется
электромагнитная волна с напряженностями
электрического и магнитного полей
соответственно ![]() и
объемной плотностью энергии
и
объемной плотностью энергии 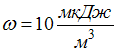 ,
равен …
,
равен …
|
|
|
2
| |
Решение:
Плотность
потока энергии электромагнитной волны
(вектор Умова – Пойнтинга) равна: 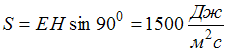 .
Также
.
Также ![]() где
где ![]() объемная
плотность энергии,
объемная
плотность энергии, ![]() скорость
электромагнитной волны в среде,
скорость
электромагнитной волны в среде, ![]() скорость
электромагнитной волны в вакууме,
скорость
электромагнитной волны в вакууме, ![]() показатель
преломления. Следовательно,
показатель
преломления. Следовательно, ![]() и
и 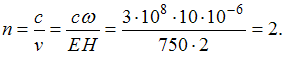
![]() ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Волны. Уравнение волны
Уравнение
плоской синусоидальной волны,
распространяющейся вдоль оси OХ, имеет
вид
ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Волны. Уравнение волны
Уравнение
плоской синусоидальной волны,
распространяющейся вдоль оси OХ, имеет
вид ![]() .
Амплитуда ускорения колебаний частиц
среды (в
.
Амплитуда ускорения колебаний частиц
среды (в ![]() )
равна …
)
равна …
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
500 |
|
|
|
|
5 |
Решение:
Уравнение
плоской синусоидальной волны имеет
вид ![]() ,
где
,
где ![]() –
амплитуда волны;
–
амплитуда волны; ![]() –
циклическая частота;
–
циклическая частота; ![]() –
период колебаний;
–
период колебаний; ![]() –
волновое число;
–
волновое число; ![]() –
длина волны; (
–
длина волны; (![]() )
– фаза волны;
)
– фаза волны; ![]() начальная
фаза. Скорость колебаний частиц среды
начальная
фаза. Скорость колебаний частиц среды ![]() .
Ускорение частиц среды
.
Ускорение частиц среды 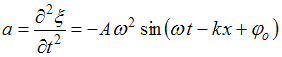 .
Амплитуда ускорения частиц среды
.
Амплитуда ускорения частиц среды ![]()
![]() ЗАДАНИЕ
N 5 сообщить
об ошибке
Тема:
Уравнения Шредингера (общие
свойства)
Стационарное
уравнение Шредингера имеет вид
ЗАДАНИЕ
N 5 сообщить
об ошибке
Тема:
Уравнения Шредингера (общие
свойства)
Стационарное
уравнение Шредингера имеет вид 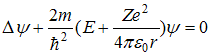 .
Это
уравнение описывает …
.
Это
уравнение описывает …
|
|
|
|
электрон в водородоподобном атоме |
|
|
|
|
движение свободной частицы |
|
|
|
|
электрон в трехмерном потенциальном ящике |
|
|
|
|
линейный гармонический осциллятор |
Решение:
Стационарное
уравнение Шредингера в общем случае
имеет вид 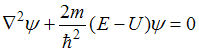 .
Здесь
.
Здесь ![]() –
потенциальная энергия микрочастицы. В
данной задаче
–
потенциальная энергия микрочастицы. В
данной задаче 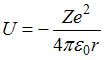 .
Это выражение представляет собой
потенциальную энергию электрона в
водородоподобном атоме. Поэтому
приведенное уравнение Шредингера
описывает электрон в водородоподобном
атоме.
.
Это выражение представляет собой
потенциальную энергию электрона в
водородоподобном атоме. Поэтому
приведенное уравнение Шредингера
описывает электрон в водородоподобном
атоме.
![]() ЗАДАНИЕ
N 6 сообщить
об ошибке
Тема:
Уравнение Шредингера (конкретные
ситуации)
Частица
находится в прямоугольном одномерном
потенциальном ящике с непроницаемыми
стенками шириной 0,2 нм.
Если энергия частицы на втором
энергетическом уровне равна 37,8 эВ,
то на четвертом энергетическом уровне
равна _____ эВ.
ЗАДАНИЕ
N 6 сообщить
об ошибке
Тема:
Уравнение Шредингера (конкретные
ситуации)
Частица
находится в прямоугольном одномерном
потенциальном ящике с непроницаемыми
стенками шириной 0,2 нм.
Если энергия частицы на втором
энергетическом уровне равна 37,8 эВ,
то на четвертом энергетическом уровне
равна _____ эВ.
|
|
|
|
151,2 |
|
|
|
|
75,6 |
|
|
|
|
18,9 |
|
|
|
|
9,45 |
Решение:
Собственные
значения энергии частицы в прямоугольном
одномерном потенциальном ящике
определяются формулой: 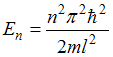 ,
где
,
где ![]() номер
энергетического уровня. Следовательно,
номер
энергетического уровня. Следовательно,  и
и ![]() .
.
![]() ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Спектр атома водорода. Правило отбора
На
рисунке схематически изображены
стационарные орбиты электрона в атоме
водорода, согласно модели Бора, а также
показаны переходы электрона с одной
стационарной орбиты на другую,
сопровождающиеся излучением кванта
энергии. В ультрафиолетовой области
спектра эти переходы дают серию Лаймана,
в видимой – серию Бальмера, в инфракрасной
– серию Пашена:
ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Спектр атома водорода. Правило отбора
На
рисунке схематически изображены
стационарные орбиты электрона в атоме
водорода, согласно модели Бора, а также
показаны переходы электрона с одной
стационарной орбиты на другую,
сопровождающиеся излучением кванта
энергии. В ультрафиолетовой области
спектра эти переходы дают серию Лаймана,
в видимой – серию Бальмера, в инфракрасной
– серию Пашена:
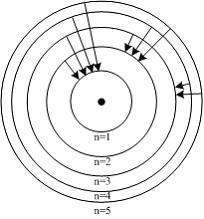 Наименьшей
частоте кванта в серии Бальмера
соответствует переход …
Наименьшей
частоте кванта в серии Бальмера
соответствует переход …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема:
Дуализм свойств микрочастиц. Соотношение
неопределенностей Гейзенберга
Отношение
скоростей протона и α-частицы,
длины волн де Бройля которых одинаковы,
равно …
ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема:
Дуализм свойств микрочастиц. Соотношение
неопределенностей Гейзенберга
Отношение
скоростей протона и α-частицы,
длины волн де Бройля которых одинаковы,
равно …
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
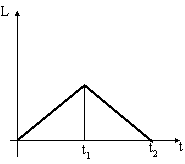
N 9 сообщить
об ошибке
Тема:
Динамика поступательного движения
На
рисунке приведен график зависимости
скорости
ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема:
Динамика поступательного движения
На
рисунке приведен график зависимости
скорости ![]() тела
от времени t.
тела
от времени t.
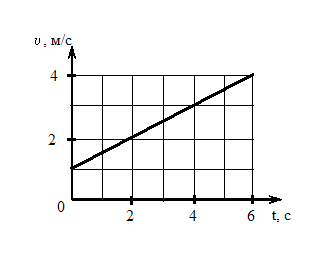 Если
масса тела равна 2 кг,
то изменение импульса тела (в единицах
СИ) за 2 с равно …
Если
масса тела равна 2 кг,
то изменение импульса тела (в единицах
СИ) за 2 с равно …
|
|
|
2 |
![]() ЗАДАНИЕ
N 10 сообщить
об ошибке
Тема:
Законы сохранения в механике
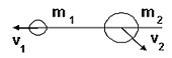
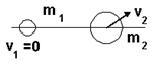
Шар
массы
ЗАДАНИЕ
N 10 сообщить
об ошибке
Тема:
Законы сохранения в механике
Шар
массы ![]() ,
имеющий скорость v,
налетает на неподвижный шар массы
,
имеющий скорость v,
налетает на неподвижный шар массы ![]() :
:
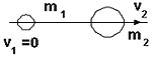
 После
соударения шары будут двигаться так,
как показано на рисунке …
После
соударения шары будут двигаться так,
как показано на рисунке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема:
Элементы специальной теории
относительности
Нестабильная
частица движется со скоростью 0,6 с (с –
скорость света в вакууме). Тогда время
ее жизни в системе отсчета, относительно
которой частица движется ______%.
ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема:
Элементы специальной теории
относительности
Нестабильная
частица движется со скоростью 0,6 с (с –
скорость света в вакууме). Тогда время
ее жизни в системе отсчета, относительно
которой частица движется ______%.
|
|
|
|
увеличится на 20 |
|
|
|
|
уменьшится на 20 |
|
|
|
|
уменьшится на 40 |
|
|
|
|
увеличится на 40 |
Решение:
Из
преобразований Лоренца следует, что в
движущейся инерциальной системе отсчета
со скоростью, сравнимой со скоростью
света, наблюдается эффект замедления
хода времени. Относительное изменение
времени жизни частицы составит:
 где
где ![]() –
скорость частицы,
–
скорость частицы, ![]() –
скорость света,
–
скорость света, ![]() время
жизни частицы в системе отсчета,
относительно которой частица
неподвижна,
время
жизни частицы в системе отсчета,
относительно которой частица
неподвижна, ![]() время
жизни частицы в системе отсчета,
относительно которой частица движется.
Следовательно, время жизни частицы
увеличится на 20%.
время
жизни частицы в системе отсчета,
относительно которой частица движется.
Следовательно, время жизни частицы
увеличится на 20%.
![]() ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Работа. Энергия
Потенциальная
энергия частицы задается
функцией
ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Работа. Энергия
Потенциальная
энергия частицы задается
функцией ![]() .
.
![]() -компонента
(в Н)
вектора силы, действующей на частицу в
точке А (3, 1, 2), равна …
(Функция
-компонента
(в Н)
вектора силы, действующей на частицу в
точке А (3, 1, 2), равна …
(Функция ![]() и
координаты точки А заданы в единицах
СИ.)
и
координаты точки А заданы в единицах
СИ.)
|
|
|
36
| |
Решение:
Связь
между потенциальной энергией частицы
и соответствующей ей потенциальной
силой имеет вид ![]() ,
или
,
или ![]() ,
, 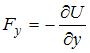 ,
, ![]() .
Таким образом,
.
Таким образом, 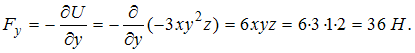
![]() ЗАДАНИЕ
N 13 сообщить
об ошибке
Тема:
Кинематика поступательного и вращательного
движения
Диск
равномерно вращается вокруг вертикальной
оси в направлении, указанном на рисунке
белой стрелкой. В некоторый момент
времени к ободу диска была приложена
сила, направленная по касательной.
ЗАДАНИЕ
N 13 сообщить
об ошибке
Тема:
Кинематика поступательного и вращательного
движения
Диск
равномерно вращается вокруг вертикальной
оси в направлении, указанном на рисунке
белой стрелкой. В некоторый момент
времени к ободу диска была приложена
сила, направленная по касательной.
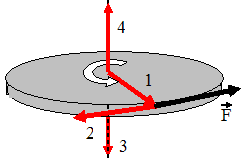 При
этом правильно изображает направление
углового ускорения диска вектор …
При
этом правильно изображает направление
углового ускорения диска вектор …
|
|
|
|
4 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
![]() ЗАДАНИЕ
N 14 сообщить
об ошибке
Тема:
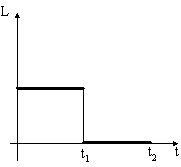
Динамика вращательного движения
Диск
начинает вращаться под действием момента
сил, график временной зависимости
которого представлен на рисунке:
ЗАДАНИЕ
N 14 сообщить
об ошибке
Тема:
Динамика вращательного движения
Диск
начинает вращаться под действием момента
сил, график временной зависимости
которого представлен на рисунке:
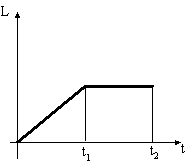
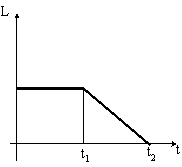
 Правильно
отражает зависимость момента импульса
диска от времени график …
Правильно
отражает зависимость момента импульса
диска от времени график …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 15 сообщить
об ошибке
Тема:
Первое начало термодинамики. Работа
при изопроцессах
Один
моль идеального одноатомного газа в
ходе некоторого процесса получил
ЗАДАНИЕ
N 15 сообщить
об ошибке
Тема:
Первое начало термодинамики. Работа
при изопроцессах
Один
моль идеального одноатомного газа в
ходе некоторого процесса получил ![]() теплоты.
При этом его температура понизилась
на
теплоты.
При этом его температура понизилась
на ![]() .
Работа (
.
Работа (![]() ),
совершенная газом, равна …
),
совершенная газом, равна … 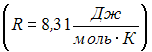
|
|
|
5000
| |
Решение:
Согласно
первому началу термодинамики, ![]() ,
где
,
где ![]() –
количество теплоты, полученное газом,
–
количество теплоты, полученное газом, ![]() –
приращение его внутренней энергии,
–
приращение его внутренней энергии, ![]() –
работа, совершенная газом. Отсюда
–
работа, совершенная газом. Отсюда ![]() .
Приращение внутренней энергии в данном
случае
.
Приращение внутренней энергии в данном
случае ![]() ,
так как температура газа в ходе процесса
понизилась.
,
так как температура газа в ходе процесса
понизилась. ![]() .
Тогда работа, совершенная газом, равна
.
Тогда работа, совершенная газом, равна ![]()
![]() ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Распределения Максвелла и Больцмана
В
трех одинаковых сосудах находится
одинаковое количество газа, причем
ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Распределения Максвелла и Больцмана
В
трех одинаковых сосудах находится
одинаковое количество газа, причем ![]()
 На
рисунке представлены графики функций
распределения молекул идеального газа
по скоростям (распределение Максвелла),
где
На
рисунке представлены графики функций
распределения молекул идеального газа
по скоростям (распределение Максвелла),
где ![]() –
доля молекул, скорости которых заключены
в интервале скоростей от
–
доля молекул, скорости которых заключены
в интервале скоростей от ![]() до
до ![]() в
расчете на единицу этого интервала.
в
расчете на единицу этого интервала.
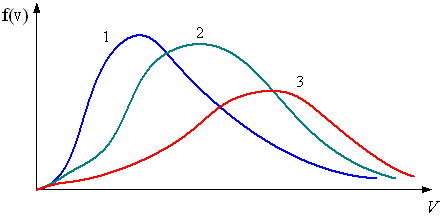 Для
этих функций верными являются утверждения,
что …
Для
этих функций верными являются утверждения,
что …
|
|
|
|
кривая
1 соответствует распределению по
скоростям молекул газа при температуре |
|
|
|
|
кривая
3 соответствует распределению по
скоростям молекул газа при температуре |
|
|
|
|
кривая
2 соответствует распределению по
скоростям молекул газа при температуре |
|
|
|
|
кривая
3 соответствует распределению по
скоростям молекул газа при температуре |
![]() ЗАДАНИЕ
N 17 сообщить
об ошибке
Тема:
Средняя энергия молекул
В
соответствии с законом равномерного
распределения энергии по степеням
свободы средняя кинетическая энергия
молекулы идеального газа при
температуре T равна:
ЗАДАНИЕ
N 17 сообщить
об ошибке
Тема:
Средняя энергия молекул
В
соответствии с законом равномерного
распределения энергии по степеням
свободы средняя кинетическая энергия
молекулы идеального газа при
температуре T равна: ![]() .
Здесь
.
Здесь ![]() ,
где
,
где ![]() ,
, ![]() и
и ![]() –
число степеней свободы поступательного,
вращательного и колебательного движений
молекулы соответственно. Для гелия (
–
число степеней свободы поступательного,
вращательного и колебательного движений
молекулы соответственно. Для гелия (![]() )
число i равно …
)
число i равно …
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
7 |
|
|
|
|
6 |
Решение:
Для
статистической системы в состоянии
термодинамического равновесия на каждую
поступательную и вращательную степени
свободы приходится в среднем кинетическая
энергия, равная ![]() ,
а на каждую колебательную степень –
,
а на каждую колебательную степень – ![]() .
Средняя кинетическая энергия молекулы
равна:
.
Средняя кинетическая энергия молекулы
равна: ![]() .
Здесь
.
Здесь ![]() –
сумма числа поступательных, вращательных
и удвоенного числа колебательных
степеней свободы молекулы:
–
сумма числа поступательных, вращательных
и удвоенного числа колебательных
степеней свободы молекулы: ![]() ,
где
,
где ![]() –
число степеней свободы поступательного
движения, равное 3;
–
число степеней свободы поступательного
движения, равное 3; ![]() –
число степеней свободы вращательного
движения, которое может быть равно 0, 2,
3;
–
число степеней свободы вращательного
движения, которое может быть равно 0, 2,
3; ![]() –
число степеней свободы колебательного
движения, минимальное количество которых
равно 1.
Для гелия
(
–
число степеней свободы колебательного
движения, минимальное количество которых
равно 1.
Для гелия
(![]() ) (одноатомной
молекулы)
) (одноатомной
молекулы) ![]() ,
, ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() .
.