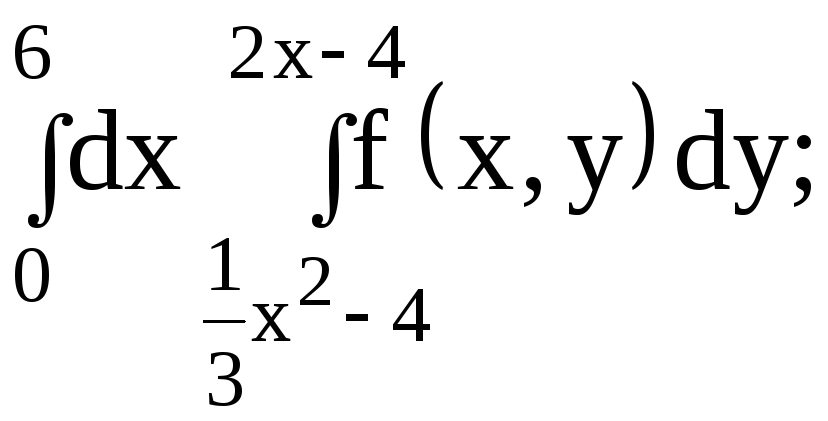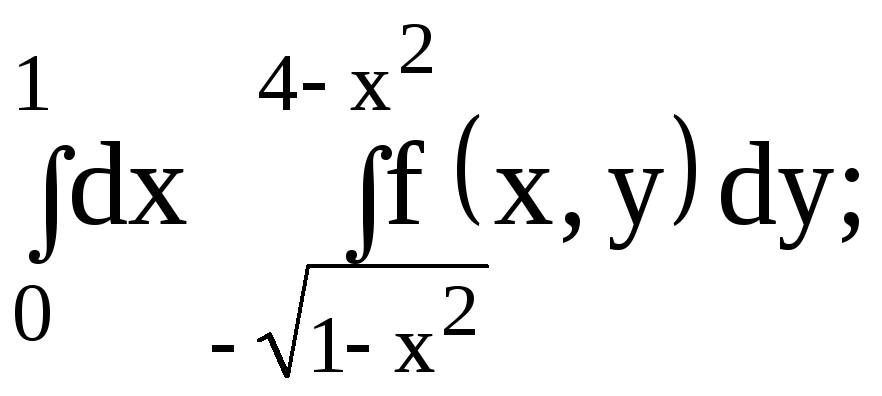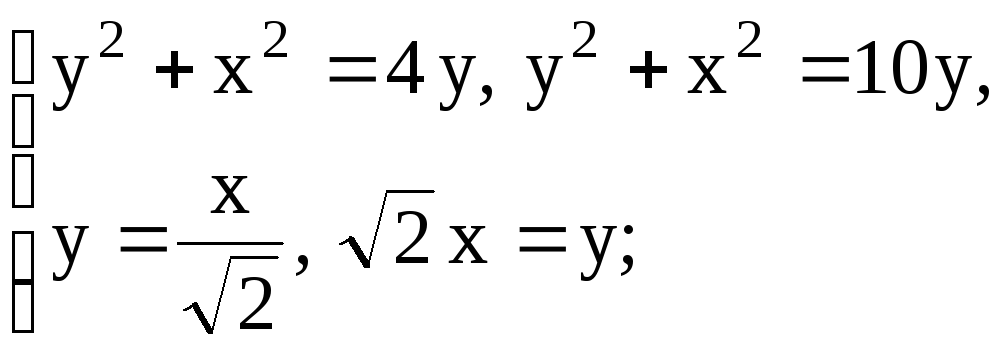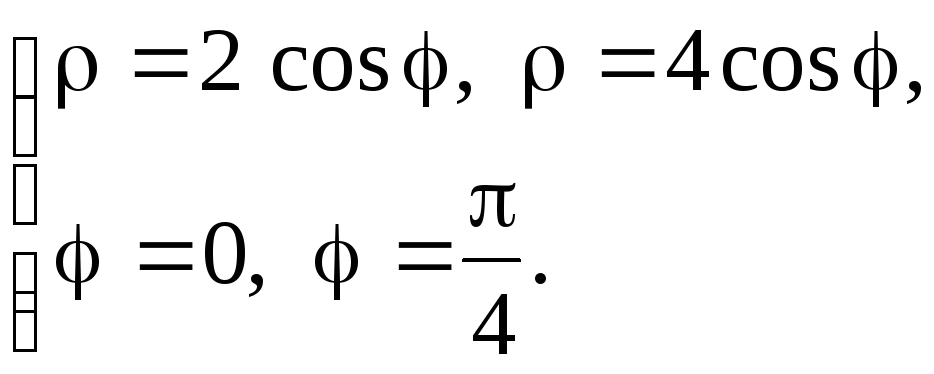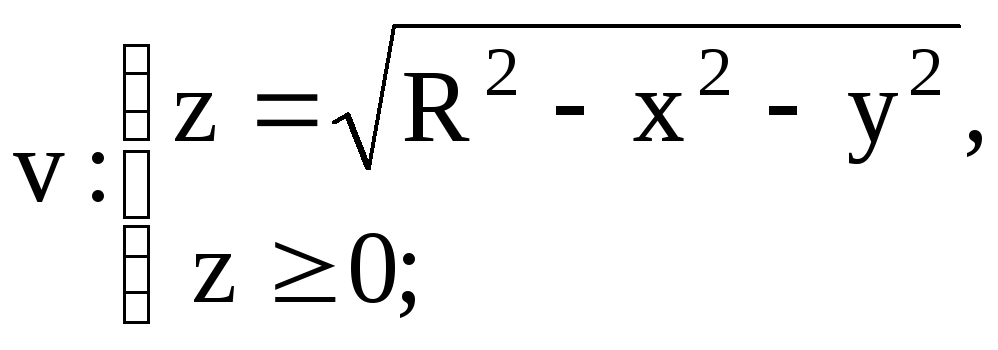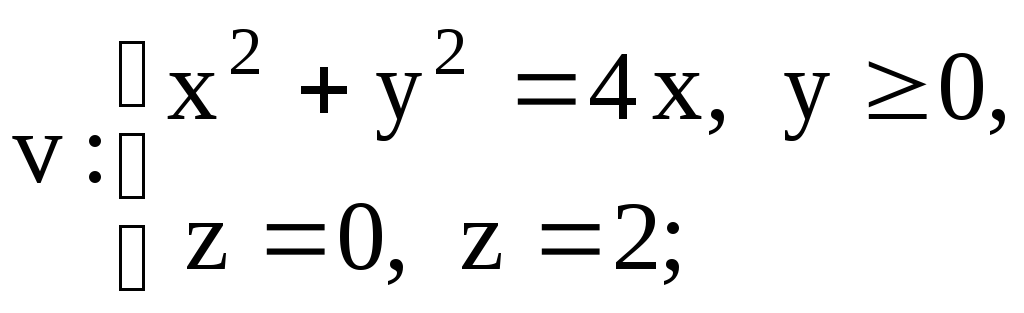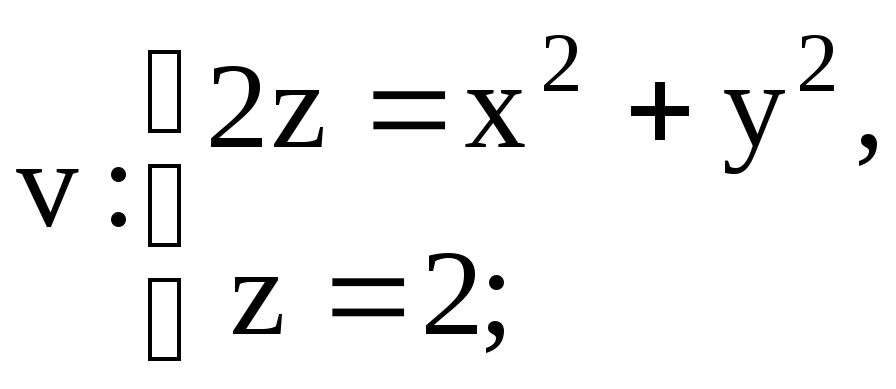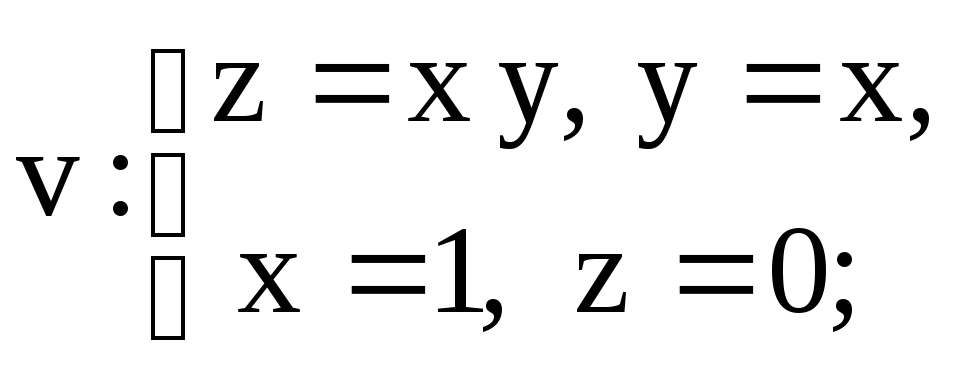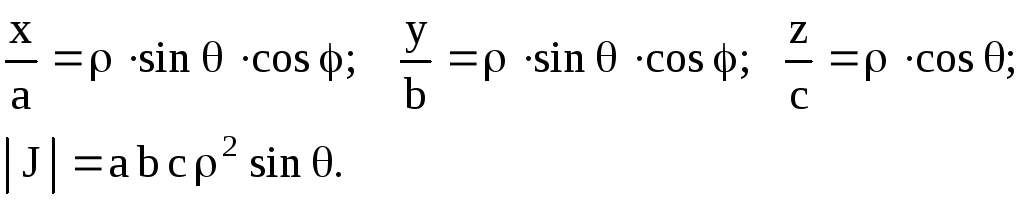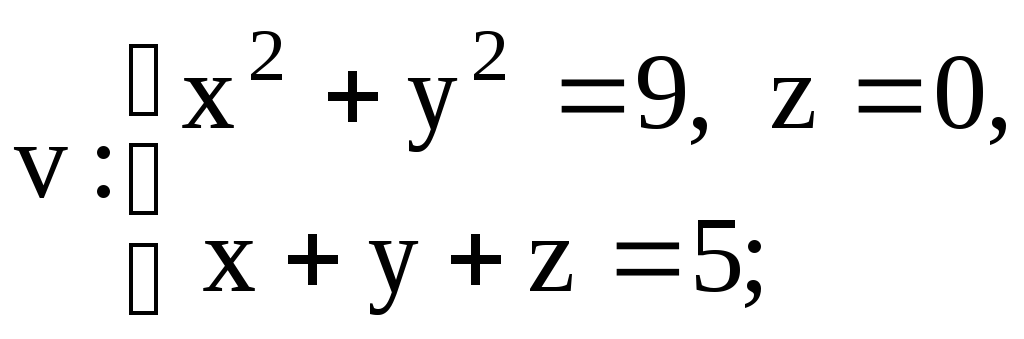Расчетные задания
1.
Вычислить
двойной интеграл
![]() по прямоугольной области
по прямоугольной области
![]() .
Нарисовать область интегрирования.
.
Нарисовать область интегрирования.
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
|
8.
|
|
|
9.
|
|
|
10.
|
|
|
11.
|
|
|
12.
|
|
|
13.
|
|
|
14.
|
|
|
15.
|
|
|
16.
|
|
|
17.
|
|
|
18.
|
|
|
19.
|
|
|
20.
|
|
|
21.
|
|
|
22.
|
|
|
23.
|
|
|
24.
|
|
|
25.
|
|
|
26.
|
|
|
27.
|
|
|
28.
|
|
|
29.
|
|
|
30.
|
|
2. Изменить порядок интегрирования. Нарисовать область интегрирования
|
1.
|
16.
|
|
2.
|
17.
|
|
3.
|
18.
|
|
4.
|
19.
|
|
5.
|
20.
|
|
6.
|
21.
|
|
7.
|
22.
|
|
8.
|
23.
|
|
9.
|
24.
|
|
10.
|
25.
|
|
11.
|
26.
|
|
12.
|
27.
|
|
13.
|
28.
|
|
14.
|
29.
|
|
15.
|
30.
|
3. Вычислить двойной интеграл и нарисовать область интегрирования
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
|
8.
|
|
|
9.
|
|
|
10.
|
|
|
11.
|
|
|
12.
|
|
|
13.
|
|
|
14.
|
|
|
15.
|
|
|
16.
|
|
|
17.
|
|
|
18.
|
|
|
19.
|
|
|
20.
|
|
|
21.
|
|
|
22.
|
|
|
23.
|
|
|
24.
|
|
|
25.
|
|
|
26.
|
|
|
27.
|
|
|
28.
|
|
|
29.
|
|
|
30.
|
|
4.
Вычислить двойной
интеграл, применяя переход в полярную
систему координат
![]() .
Нарисовать область интегрирования.
.
Нарисовать область интегрирования.
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
|
8.
|
|
|
9.
|
|
|
10.
|
|
|
11.
|
|
|
12.
|
|
|
13.
|
|
|
14.
|
|
|
15.
|
|
|
16.
|
|
|
17.
|
|
|
18.
|
|
|
19.
|
|
|
20.
|
|
|
21.
|
указание: полагаем:
|
|
22.
|
|
|
23.
|
|
|
24.
|
|
|
|
Указание: полагаем
|
|
25.
|
|
|
26.
|
|
|
27.
|
|
|
28.
|
|
|
29.
|
|
|
30.
|
|
5. Найти площадь фигуры, ограниченной данными линиями с помощью двойного интеграла. (Перейти в полярную систему координат, сделать рисунок в полярной системе координат).
|
1.
|
16.
|
|
2.
|
17.
|
|
3.
|
18.
Указание:
|
|
4.
|
19.
|
|
5.
|
20.
|
|
6.
|
21.
|
|
7.
|
22.
|
|
8.
|
23.
|
|
9.
|
24.
|
|
10.
|
25.
|
|
11.
|
26.
|
|
12.
|
27.
|
|
13.
|
28.
|
|
14.
|
29.
|
|
15.
|
30.
|
6. Найти центр тяжести плоской пластинки, ограниченной данными линиями, с помощью двойного интеграла
-
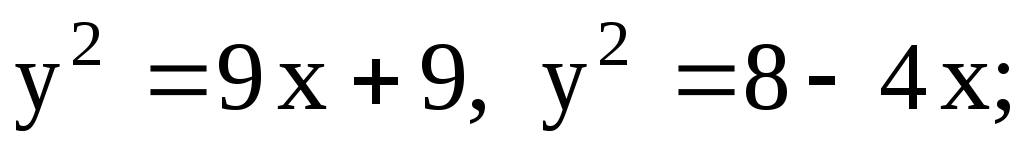
-

-

-

-

-

-

-

-

-

-

-
 (астроида)
(астроида)

-

-

-
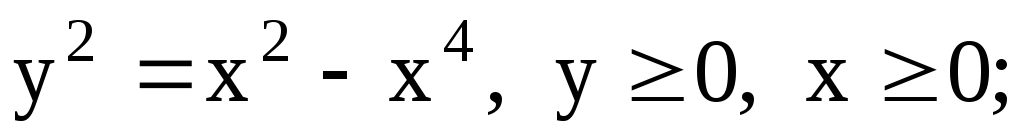
-

-

-

-

-

-
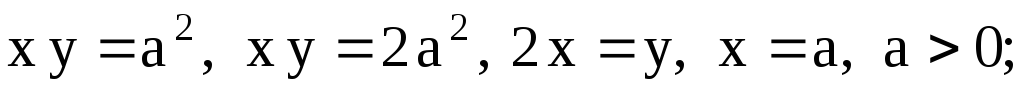
-

-

-

-
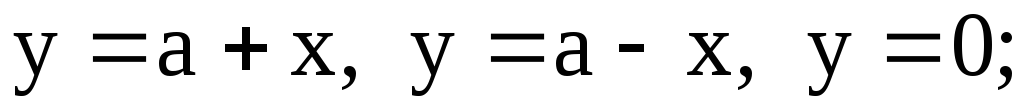
-

27.
![]()
28.
![]()
29.
![]() (перейти в полярную систему координат);
(перейти в полярную систему координат);
30.
![]() (перейти в полярную систему координат).
(перейти в полярную систему координат).
7. Найти объем тела,
ограниченного указанными поверхностями,
с помощью двойного интеграла:
![]()
-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-
 здесь
(при вычислении двойного интеграла)
надо сделать переход в полярную систему
координат по формулам:
здесь
(при вычислении двойного интеграла)
надо сделать переход в полярную систему
координат по формулам:

 .
Не забыть вычислить Якобиан.
.
Не забыть вычислить Якобиан.
-

-

-

-

-


-

-

-

-


-

-
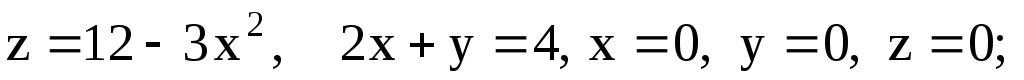
-

-

-

![]() При вычислении
двойного интеграла перейти в полярную
систему координат.
При вычислении
двойного интеграла перейти в полярную
систему координат.
8 Вычислить тройной
интеграл по заданной области интегрирования
![]()
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
|
8.
|
|
|
9.
|
|
|
10
.
|
|
|
11.
|
|
|
12.
|
|
|
13.
|
|
|
14.
|
|
|
15.
|
|
|
16.
|
|
|
17.
|
|
|
18.
|
|
|
19.
|
|
|
20.
|
|
|
21.
|
|
|
22.
|
|
|
23.
|
|
|
24.
|
|
|
25.
|
|
|
|
|
|
26.
|
|
|
27.
|
|
|
28.
|
|
|
29.
|
|
|
30.
|
|
9 Найти объем тела,
заданного ограничивающими их поверхностями,
с помощью тройного интеграла:
![]()
![]() Сделать переход
в сферическую систему координат по
формулам:
Сделать переход
в сферическую систему координат по
формулам:
![]()
-

-
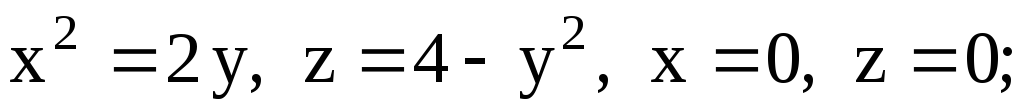
-

-
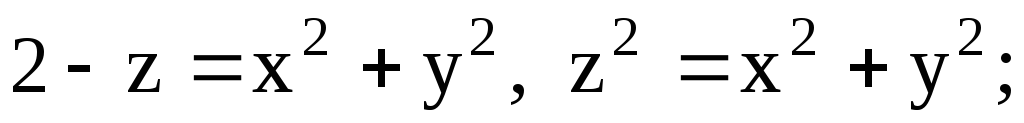
-

-

-

-

-

-

-

-

-

-

-

-
 (внутренний объем
по отношению к параболоиду);
(внутренний объем
по отношению к параболоиду); -
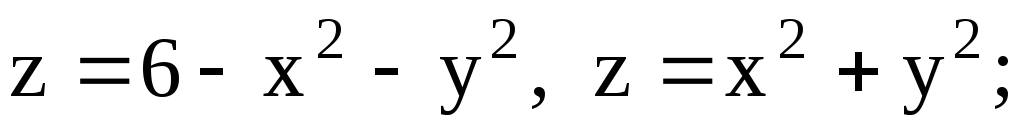
-

-

-
 (вне конуса).
(вне конуса).
10. Тело задано
ограничивающими его поверхностями,
![]() плотность массы тела. Найти центр тяжести
тела с помощью тройного интеграла
плотность массы тела. Найти центр тяжести
тела с помощью тройного интеграла