34. Метод линеаризации

Имеется последовательность k-мерных случайных векторов X_n = (X_1n, X_2n, … , X_kn), n = 1, 2, … , такая, что X_n → a = (a₁, a₂, … , a_k) при n → ∞, и последовательность функций f_n: R^k → R¹. Требуется найти распределение случайной величины f_n(X_n).

          Основная идея – рассмотреть главный линейный член функции f_n в окрестности точки а. Из математического анализа известно, что

,

где остаточный член является бесконечно малой величиной более высокого порядка малости, чем линейный член. Таким образом, произвольная функция может быть заменена на линейную функцию от координат случайного вектора. Эта замена проводится с точностью до бесконечно малых более высокого порядка. Конечно, должны быть выполнены некоторые математические условия регулярности. Например, функции f_n должны быть дважды непрерывно дифференцируемы в окрестности точки а.

          Если вектор X_n  является асимптотически нормальным с математическим ожиданием а и ковариационной матрицей ∑/n, где ∑ = ||σ_ij||, причем σ_ij = nM(X_i – a_i)(X_j – a_j), то линейная функция от его координат также асимптотически нормальна. Следовательно, при очевидных условиях регулярности f_n(X_n) – асимптотически нормальная случайная величина с математическим ожиданиемf_n(а) и дисперсией

.

          Для практического использования асимптотической нормальности f_n(X_n) остается заменить неизвестные моменты а и ∑ на их оценки. Например, если X_n – это среднее арифметическое независимых одинаково распределенных случайных векторов, то а можно заменить на X_n, а ∑ - на выборочную ковариационную матрицу.

          Пример. Пусть Y₁, Y₂, … , Y_n – независимые одинаково распределенные случайные величины с математическим ожиданием а и дисперсией σ². В качестве X_n (k = 1) рассмотрим выборочное среднее арифметическое

.

Как известно, в силу закона больших чисел → а = М(У). Следовательно, для получения распределений функций от выборочного среднего арифметического можно использовать метод линеаризации. В качестве примера рассмотрим f_n(y) = f(y) = y². Тогда

.

Из этого соотношения следует, что с точностью до бесконечно малых более высокого порядка

.

Поскольку в соответствии с Центральной Предельной Теоремой выборочное среднее арифметическое является асимптотически нормальной случайной величиной с математическим ожиданием а и дисперсией σ²/n, то квадрат этой статистики является асимптотически нормальной случайной величиной с математическим ожиданием а² и дисперсией 4а²σ²/n. Для практического использования может оказаться полезной замена параметров (асимптотического нормального распределения) на их оценки, а именно, математического ожидания – на , а дисперсии – на , где s² – выборочная дисперсия.

35. Коэффициент детерминации. Коэффициент конкордации

Коэффициент детерминации

Подбор функции линейной регрессии осуществляется на основе соображений профессионально-теоретического характера, а вычисленные оценки параметров, входящие в уравнения регрессии, наиболее хорошо согласовывались с опытными данными. Критерий соответствия регрессии опытным данным заложен в требовании наименьших квадратов:

(1)

Результаты различных выборок имеют различное рассеяние. Поэтому может случиться, что построение регрессионной зависимости одного и того же экономического смысла по данным двух выборок из одной и той же генеральной совокупности приведет к различным уравнениям. Степень соответствия этих уравнений опытным данным, несмотря на одинаковый тип зависимости, может быть различна. Однако критерий (1) имеет недостаток: хотя его нижняя граница равна нулю, верхняя граница не может быть указана. Поэтому для оценки степени соответствия регрессии имеющимся эмпирическим данным он не используется. Желательно иметь в распоряжении показатель, отражающий, в какой мере функция регрессии определяется объясняющими переменными, содержащимися в ней. В качестве такого показателя можно выбрать коэффициент детерминации.

Рассмотрим вначале коэффициент детерминации для простой линейной регрессии, называемый также коэффициентом парной детерминации.

На основе соображений, изложенных в разделе 1, теперь отно­сительно легко найти меру точности оценки регрессии. Было показано, что общую дисперсию можно разложить на две составляющие — на «необъясненную» дисперсиюи дисперсию, обусловленную регрес­сией. Чем большепо сравнению с, тем больше общая дисперсия формируется за счет влияния объясняющей переменнойx и, следова­тельно, связь между двумя переменнымиyиx более интенсивная. Очевидно, удобно в качестве показателя интенсивности связи, или оценки доли влияния переменнойxнаy, использовать отношение

(7)

Это отношение указывает, какая часть общего (полного) рассеяния значений уобусловлена изменчивостью переменнойx. Чем большую долю в общей дисперсии составляет, тем лучше выбранная функция регрессии соответствует эмпирическим данным. Чем меньше эмпири-ческие значения зависимой переменной отклоняются от прямой регрес-сии, тем лучше определена функция регрессии. Отсюда происходит и название отношения (7) — коэффициент детерминации. Индекс при коэффициенте указывает на переменные, связь между которыми изучается. При этом вначале в индексе стоит обозначение зависимой переменной, а затем объясняющей.

Из определения коэффициента детерминации как относительной доли очевидно, что он всегда заключен в пределах от 0 до 1:

(8)

Если , то все эмпирические значения(все точки поля корреляции) лежат на регрессионной прямой. Это означает, чтодляi=1, ..., n, т. е.. В этом случае говорят о строгом линейном соотношении (линейной функции) между переменнымиуих. Если, дисперсия, обусловленная регрессией, равна нулю, а «необъясненная» дисперсия равна общей дисперсии. В этом случае. Линия регрессии тогда параллельна оси абсцисс. Ни о какой численной линейной зависимости переменнойуотхв статистическом ее понимании не может быть и речи. Коэффициент регрессии при этом незначимо отличается от нуля.

Итак, чем больше приближается к единице, тем лучше опре-делена регрессия.

Коэффициент детерминации есть величина безразмерная и поэтому он не зависит от изменения единиц измерения переменных уиx(в отличие от параметров регрессии). Коэффициентне реагирует на преобразование переменных.

Приведем некоторые модификации формулы (7), которые, с одной стороны, будут способствовать пониманию сущности коэффициента де-терминации, а с другой стороны, окажутся полезными для практических вычислений. Подставляя выражение для () в (7) и принимая во внимание () и (2), получим:

(9)

Эта формула еще раз подтверждает, что «объясненная» дисперсия, стоящая в числителе (7), пропорциональна дисперсии переменной х, так какb₁является оценкой параметра регрессии.

Подставив вместо его выражение () и учитывая определения дисперсийи, а также среднихи, получим формулу коэффициента детерминации, удобную для вычисления:

или

(10)

Из (10) следует, что всегда . С помощью (10) можно относительно легко определить коэффициент детерминации. В этой формуле содержатся только те величины, которые используются для вычисления оценок параметров регрессии и, следовательно, имеются в рабочей таблице. Формула (10) обладает тем преимуществом, что вычисление коэффициента детерминации по ней производится непосредственно по эмпирическим данным. Не нужно заранее находить оценки параметров и значения регрессии. Это обстоятельство играет немаловажную роль для последующих исследований, так как перед проведением регрессионного анализа мы можем проверить, в какой степени определена исследуемая регрессия включенными в нее объясняющими переменными. Если коэффициент детерминации слишком мал, то нужно искать другие факторы-переменные, причинно обусловливающие зависимую переменную. Следует отметить, что коэффициент детерминации удовлетворительно отвечает своему назначению при достаточно большом числе наблюдений. Но в любом случае необходимо проверить значимость коэффициента детерминации.

Для решения системы нормальных уравнений очень важно знать соотношения между объясняющими переменными x_k. Используя понятие коэффициента детерминации, введем меру зависимости этих переменных между собой. Обозначим черезкоэффициент детерминации, характеризующий степень обусловленностиk-й объясняющей переменной остальными объясняющими переменными, входящими в данную регрессию.

Укажем формулу для вычисления коэффициента детерминации между объясняющими переменными. Для ее вывода исходят из матрицы дисперсий и ковариаций объясняющих переменных :

(31)

где - дисперсия объясняющей переменнойx_k,апри- ковариация объясняющих переменныхx_k и x_l. Умножив каждый элемент (31) наn-1, получим матрицусумм квадратов отклонений и произведений отклонений:

(32)

где , а. Матрицу, обратную к, обозначим через:

(33)

Коэффициент детерминации между объясняющими переменными вычисляется по формуле

(34)

где и— элементыk-й строки иk-гo столбца матрицисоответственно.

КОЭФФИЦИЕНТ КОНКОРДАЦИИ

В экономике существует большое число причинно обусловленных явлений, признаки которых не поддаются точной количественной оценке. Это так называемые атрибутивные признаки. Например, про­фессия, форма собственности, качество изделия, технологические опера­ции и т. д. Специалист или эксперт ранжирует элементы изучаемой со­вокупности, приписывая каждому из них порядковый номер, соответст­вующий итогам сравнения по данному признаку с остальными элемен­тами. Если количество признаков-переменных больше двух, то в ре­зультате ранжировок n элементов (предприятий или учреждений) имеют дело с m последовательностями рангов. Для проверки, хорошо ли согласуются эти m ранжировок друг с другом, используется коэф­фициент согласованности W, называемый также коэффициентом конкордации Кендэла:

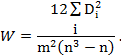
При наличии связанных рангoв коэффициент кенкордации W вычис­ляется по формуле

где i= 1, 2, ....,n;j= 1, 2, ....,m- суммарангов, приписанных всеми экспертами t-му элементу выборки, минус среднее значение этих сумм рангов; m — число экспертов или призна­ков, связь между которыми оценивается; n — объем выборки (числопредприятий или учреждений), другими словами, это количество членов последовательности рангов; , где - число связанных рангов, к = 1, ... z. Например, если связываются элементы от восьмого до одиннадцатого включительно, то = 4. Коэффи­циент W принимает значения в интервале 0 ≤ W ≤ 1.