1.5.1.2 Развертка поверхности пирамиды

Боковые грани пирамиды – треугольники, каждый из которых может быть построен по трем сторонам. Поэтому для получения развертки пирамиды достаточно определить натуральные величины ее боковых ребер и сторон основания.

Развертка пирамиды осуществляется в следующем порядке:

1) Определяют истинную величину боковых ребер пирамиды любым из известных способов преобразования (рисунок 1.5.6). В данном примере натуральные величины длин боковых ребер найдены способом вращения, и способом замены плоскостей проекций определена натуральная величина основания пирамиды – четырехугольника ABCD в соответствии с рисунком 1.5.6.

2) Для построения развертки боковых граней пирамиды строят натуральную величину одной из них, ограниченную натуральными величинами соответствующих ребер, взятых из предыдущих построений, например S₀A₀B₀, пристраивая к ней следующую S₀B₀C₀, а затем и остальные грани в соответствии с рисунком 1.5.7.

3) Для построения полной развертки достраивается основание пирамиды A₀B₀C₀D₀.

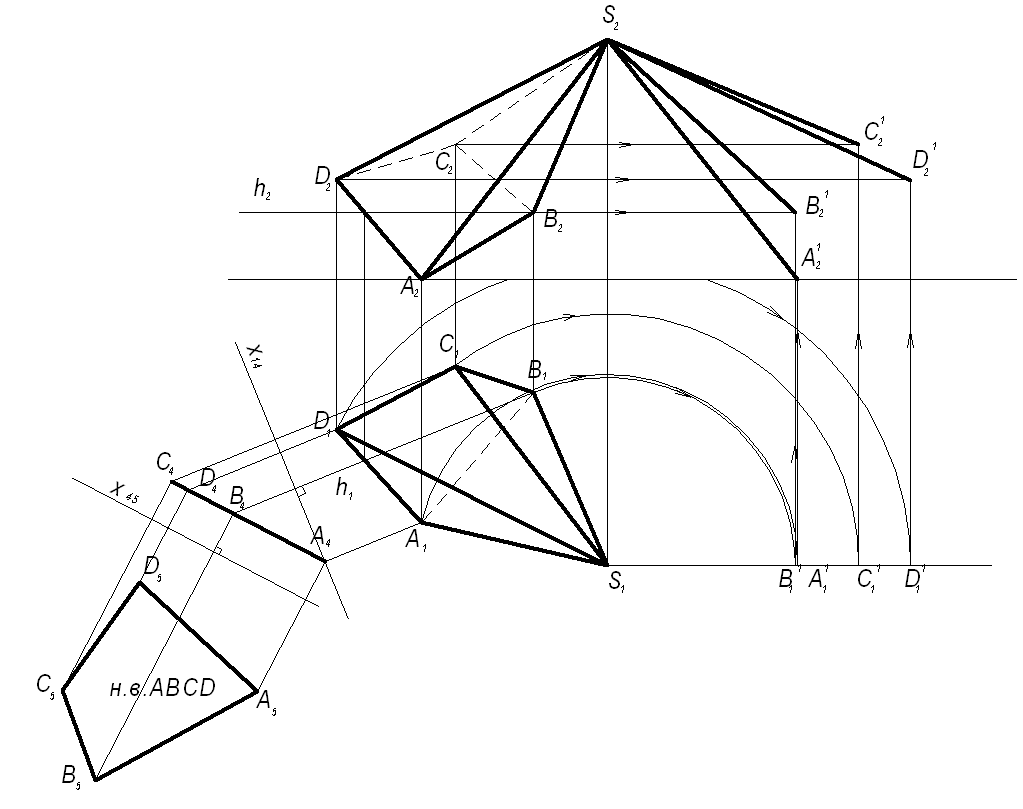
Рисунок 1.5.6

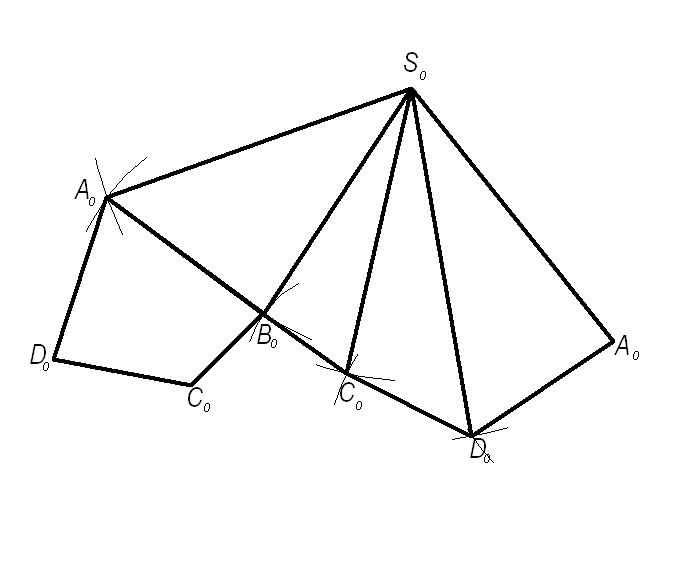
Рисунок 1.5.7 - Развертка пирамиды

1.5.2 Развертка развертываемых кривых поверхностей

1.5.2.1 Развертка цилиндрической поверхности

Цилиндрические поверхности развертываются теми же способами, что и призматические. Предварительно в заданный цилиндр вписывают n-угольную призму, а затем определяют развертку данной поверхности способом «нормального сечения» или способом «раскатки».

Если эта поверхность – прямой круговой цилиндр, то данную задачу целесообразней решить способом «нормального сечения»

На рисунке 1.5.8 изображен усеченный прямой круговой цилиндр. Так как нижнее основание цилиндра лежит в плоскости П₁, то его можно рассматривать как плоскость нормального сечения данной поверхности. Горизонтальная проекция нижнего основания совпадает с горизонтальной проекцией цилиндра, поэтому натуральной величиной периметра нормального сечения является длина окружности основания.

Для построения точки C₀ развертки откладывается отрезок B₀D₀ равный длине отрезка B₁D₁. Остальные точки развертки построены аналогично.

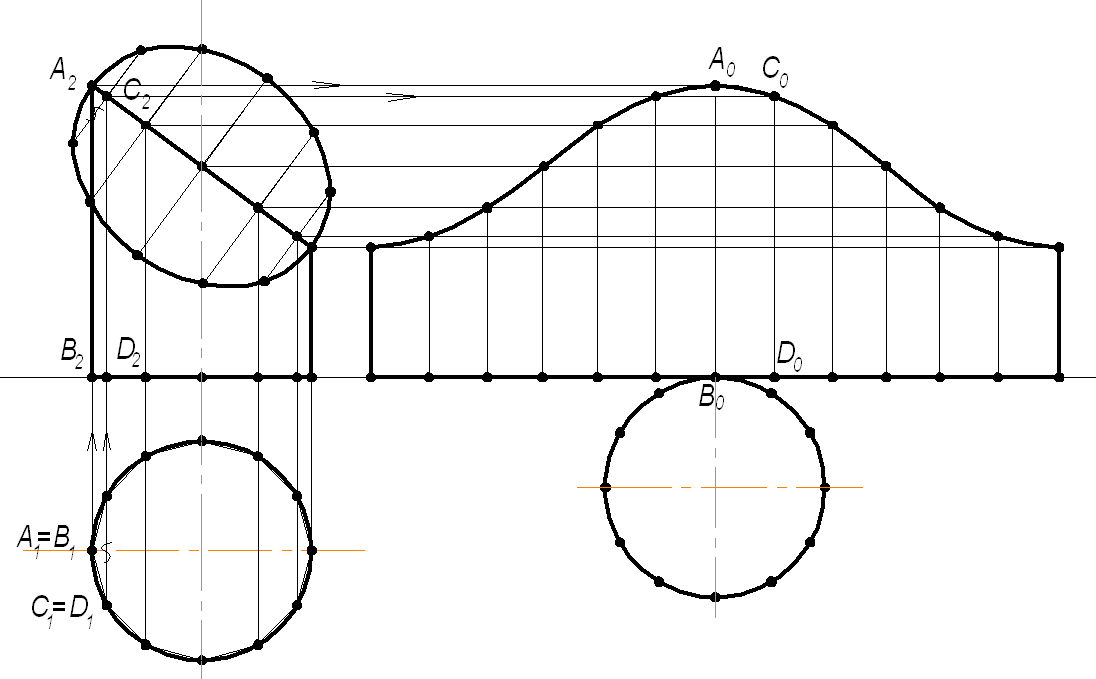
Рисунок 1.5.8 – Развертка цилиндрической поверхности способом «нормального сечения»

Если цилиндр наклонный круговой или эллиптический, то развертку такой поверхности можно построить способом «раскатки». Параллельность образующих цилиндра плоскости П₂ делает возможным выполнить развертку без предварительного преобразования проекций в соответствии с рисунком 1.5.9.

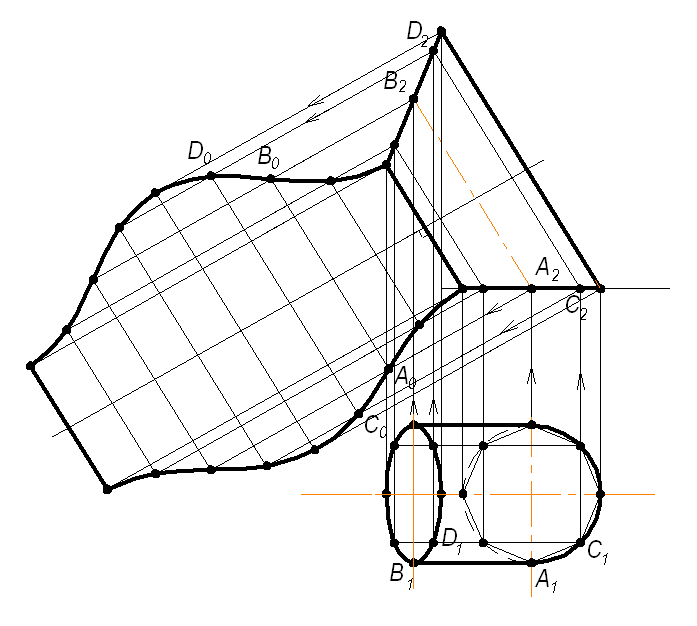
Рисунок 1.5.9 – Развертка боковой поверхности цилиндра способом «раскатки»

1.5.2.2 Развертка конической поверхности

Развертка конической поверхности выполняется аналогично развертке пирамиды в следующем порядке. Сначала в заданный конус вписывают n-угольную пирамиду (число n от масштабов и размеров чертежа, следует брать в пределах от 8 до 12). Затем строят развертку боковой поверхности вписанной пирамиды в соответствии с рисунком 1.5.10. Соединив концы ребер плавной кривой, получают приближенную развертку боковой поверхности конуса.

В данном примере выполнено построение развертки наклонного эллиптического конуса, заданного круговым основанием, лежащим в горизонтальной плоскости, и вершиной S. Натуральная величина боковых ребер вписанной восьмиугольной пирамиды найдена способом вращения.

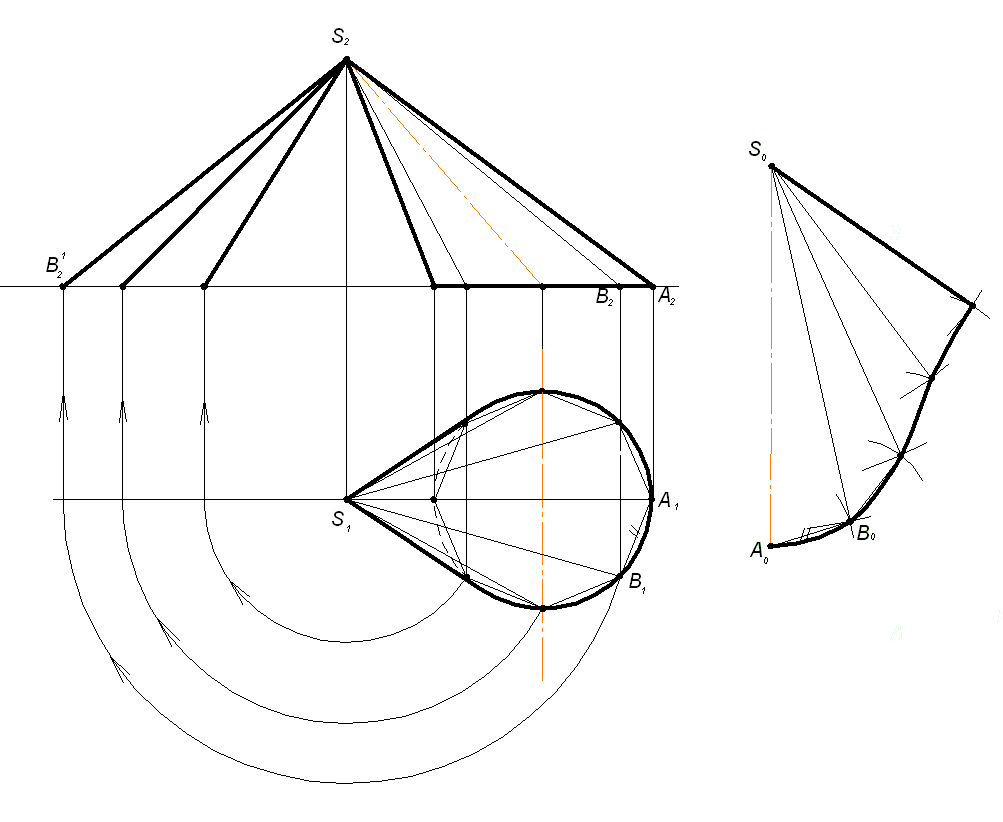
Рисунок 1.5.10 – Развертка боковой поверхности

конуса